Ryhmätyöskentelyä lukion geometriassa
”Eihän varsinkaan pitkässä matematiikassa ehdi tekemään ryhmätöitä, kun opintojaksoissa on niin paljon asiaa”, on todennäköisesti monen lukio-opettajan ensimmäinen ajatus ryhmätöiden teettämisestä matematiikassa. Uuden opiskelumenetelmän kokeilu vie aina enemmän aikaa kuin mitä perinteiseen tapaan opiskelemalla menisi, ja mikä edes voisi olla ryhmätyön aihe matematiikassa, kun oppimateriaalien tehtävät on suunniteltu pääosin itsekseen tai korkeintaan kaverin kanssa ratkaistavaksi? Lisäksi ryhmätyöt alkavat usein sillä, että pienryhmässä sovitaan, kuka tekee työstä minkäkin osion, jolloin ryhmätyö ei olekaan ryhmässä työskentelyä, ja loppujen lopuksi jokainen oppii aiheesta vain itse tekemänsä osion.
Koska ryhmätyöskentelyn käytöstä oli kuitenkin saatu hyviä kokemuksia yliopistomatematiikan kursseilla ja tutkimusten mukaan ryhmätyöskentely auttaa myös sisällön syvemmässä omaksumisessa, halusimme edellä mainituista epäilyistä huolimatta kokeilla ryhmätöitä lukion pitkässä matematiikassa syksyllä 2022. Ryhmätöitä tehtiin useilla oppitunneilla ja opiskelijat asettuivat ryhmätyöskentelyssä erilaisiin, annettuihin rooleihin. Ryhmätyöt lisäsivät opiskelijoiden keskustelua matematiikasta sekä yllättäen myös vähensivät kiireen tunnetta opintojaksolla.
Tämä kokeilu tehtiin osana yliopistopedagogiikan opintojen opetusharjoittelua, jossa yliopisto-opetusta paljon tutkinut ja opettanut matemaatikko Jokke Häsä perehtyi lukiossa opettamiseen. Harjoittelun ohjaavana opettajana toimi Mäkelänrinteen lukion matematiikan opettaja Piia Vikberg, joka on pitkään käyttänyt opiskelijalähtöisiä opiskelumenetelmiä omassa opetuksessaan ja tehnyt yhteistyötä Helsingin yliopiston matematiikan aineenopettajakoulutuksen kanssa.
Odotimme ryhmätyöskentelyltä monenlaisia hyötyjä
Molemmilla opettajilla oli halu kokeilla uutta opetusharjoittelun yhteydessä. Jokke oli tutustunut yhteistoiminnalliseen oppimiseen jo aiemmin pedagogisissa opinnoissaan sekä myös osallistunut toisten matematiikan yliopisto-opettajien kanssa ryhmätyöskentelyn suunnitteluun. Piia puolestaan oli opettanut lukiossa jo pitkään opiskelijalähtöisillä menetelmillä, mutta kaipasi uusia ideoita, joilla saisi luokassa lisättyä matemaattista ajattelua ja keskustelua. Niinpä tulimme harjoittelua suunnitellessamme siihen tulokseen, että yhtenä painopisteenä tulisi olemaan ryhmätyöskentelyn toteuttaminen lukion geometrian opintojaksolla.
Ryhmätyöskentely valikoitui kokeilumme kohteeksi monestakin syystä. Ensisijaisesti halusimme saada opiskelijat harjoittelemaan omien matemaattisten ajatustensa ilmaisemista. Luultavasti kaikille matematiikan opettajille on tuttu tilanne, jossa opettaja kysyy luokan edessä opiskelijoilta ideoita jonkin tehtävän ratkaisemiseen, mutta vastassa on vain ahdistava hiljaisuus ja katseet kiertelevät pitkin seiniä. Tämä johtuu usein siitä, että luokan ilmapiiri ei ole tarpeeksi turvallinen, jotta oppilaat uskaltaisivat ilmaista keskeneräisiä tai mahdollisesti virheellisiä ajatuksiaan. Pienessä vertaisryhmässä kynnys ei ole niin korkea, ja kun muutama ryhmäläinen on avannut suunsa, toiset saattavat huomata, että heidän omat ajatuksensa eivät olekaan sen huonompia. Lisäksi kun ryhmä toimii yhdessä tehtävän ratkaisemiseksi, heidän on helpompaa myös esittää ajatuksensa opettajalle, koska kukaan tietty ryhmäläinen ei ole niistä yksin vastuussa.
Ryhmätyöskentelyyn kannustetaan myös lukion opetussuunnitelman perusteissa [1]. Siellä todetaan, että matematiikan ”opetuksessa käytetään vaihtelevia työtapoja, joissa opiskelijat työskentelevät yksin ja yhdessä. Tällä vahvistetaan muun muassa vuorovaikutusosaamista” (s. 221). Lisäksi matematiikan opetuksen tehtävänä on muun muassa ohjata opiskelijaa ”käyttämään puhuttua, kirjoitettua ja muutoin ilmaistua matematiikkaa” (s. 221) sekä ”keskustelemaan matematiikasta ja perustelemaan väitteitä” (s. 222). Näitä vuorovaikutustaitoja voisi mielestämme tukea ohjatulla ryhmätyöskentelyllä. Lisäksi ryhmässä esiintyy luonnollisesti erilaisia ratkaisutapoja, joita ryhmäläisten täytyisi tutkia, perustella ja vertailla, jotta he voisivat tulla yhteiseen lopputulokseen. Tämäkin olisi lukio-opiskelussa toivottua toimintaa, koska opetussuunnitelman perusteiden mukaan matematiikan ”opetustilanteet järjestetään siten, että ne herättävät opiskelijan tekemään havaintojensa pohjalta kysymyksiä, oletuksia ja päätelmiä sekä perustelemaan niitä” (s. 221).
Myös pedagoginen tutkimus on osoittanut ryhmätyöskentelyn olevan hyödyksi oppimiselle. Esimerkiksi David ja Roger Johnsonin yhteistoiminnallisen oppimisen malliin (cooperative learning, [2]) viitataan usein, kun halutaan tuoda opetukseen hyvin toimivia ryhmätyömenetelmiä. Mallin mukaan hyvä ryhmätyöskentely edellyttää, että ryhmän jäsenet ovat riippuvaisia toisistaan ja tukevat toisiaan, jokaisen jäsenen panos on tärkeä tehtävän ratkaisemiseksi ja että ryhmät pääsevät arvioimaan omaan toimintaansa ja kehittämään ryhmätyötaitojaan. Robert Slavinin mukaan oppimisen hyödyt perustuvat tällaisessa mallissa toisaalta siihen, että oppilaat ovat motivoituneita oppimaan itse ja tukemaan muiden ryhmäläistensä oppimista, ja toisaalta siihen, että ryhmässä he joutuvat selittämään asioita toisilleen, miettimään perusteluja omille ajatuksilleen sekä arvioimaan toistensa näkökulmia [3,4]. Useat tutkimukset ovat osoittaneet mallin tukevan oppimisen lisäksi oppilaiden motivaatiota, sosiaalisia taitoja sekä henkilökohtaista kehittymistä [5].
Tehtävä, ajoitus ja ryhmätyön roolit oli suunniteltava huolella
Päätimme teettää opintojaksossa kaksi ryhmätyötä, jotta itse ryhmässä toimimista ehdittäisiin harjoitella riittävästi. Hyvä yhteistyö ei nimittäin suju itsestään. Suunnittelimme aikataulun niin, että ryhmätyötä ehdittäisiin tehdä useammalla kuin yhdellä viikolla muun opetuksen lomassa. Tällä tavoin ryhmätyö loisi opintojaksoon muiden aiheiden joukkoon pitkäjänteisempää pohdintaa ja keskustelua yhden teeman ympärille.
Ryhmäkooksi päätimme valita 4–5 henkilöä, jotta todennäköisesti ainakin muutama olisi aina paikalla joka ryhmästä. (Mäkelänrinteen lukio on urheilulukio ja poissaoloja tulee paljon erilaisten harjoitusten ja kilpailujen takia.) Annoimme ryhmien muodostua itsestään saman pöydän ääressä istuvista. Kurssin aluksi Piia sopi opiskelijoiden kanssa, millä tavalla ryhmätyö vaikuttaisi arviointiin, ja päätettiin, että sen painoarvo olisi 40
Ensimmäisen työn aiheeksi valitsimme pinta-alojen hahmottamisen kuvioita pilkkomalla ja toisen työn aiheeksi avaruuskappaleiden tilavuudet. Jokke suunnitteli tehtäväkokonaisuudet käyttäen hyväksi kokemustaan projektitöiden suunnittelusta yliopistokursseille. Tehtävissä oli kaksi osiota, joissa kummassakin oli porrastetusti vaikeampia osatehtäviä, ja opiskelijoita ohjeistettiin tekemään oman valintansa mukaan kumpaakin tehtävää niin pitkälle kuin he itse ryhmässä halusivat. Tehtävät sisälsivät myös matemaattista todistamista, jota lukiossa yleensä harjoitellaan vähemmän.
Kuvassa 1 näkyy ensimmäisen ryhmätyön tehtävänannon alku. Tehtävät A ja B sisältävät osatehtäviä, joista ryhmä saa valita mieleisensä palautettavaksi. Ajatuksena oli, että ryhmät voivat valita palautettavan tehtävän oman tasonsa ja kunnianhimonsa mukaisesti. Tehtävä A ohjaa opiskelijoita todistamiseen mukaillen oppikirjan tekstiä ja tunnilla esitettyjä esimerkkejä. Tässä tehtävässä opiskelijoiden suurin haaste oli oletusten ja perustelujen asettaminen oikeaan järjestykseen, jotta todistettu sääntö pätisi mielivaltaiselle kolmiolle.

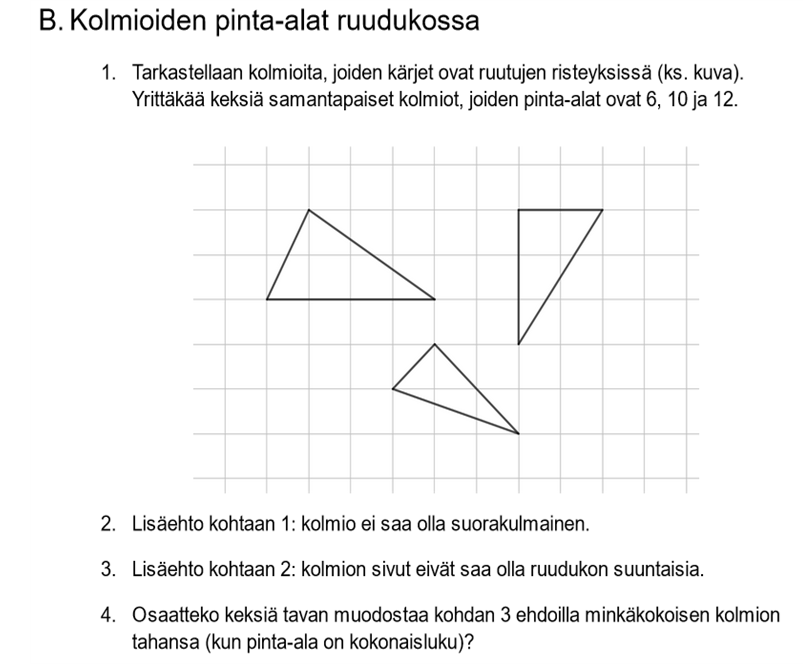
Tehtävään B (kuva 2) valittiin avoin tehtävänanto, jonka tarkoitus oli tukea opiskelijoiden kekseliäisyyttä ja luovuutta. Tehtävässä pyydetään löytämään tietynlaisia kolmioita vaikkapa kokeilemalla, mutta ajatuksena on, että osatehtävien vaikeutuessa opiskelijoiden täytyy keksiä yleisiä sääntöjä kolmioiden löytämiseksi. Tässä tehtävässä opiskelijat käyttivät ahkerasti apuna GeoGebra-ohjelmaa, jolloin haasteena oli vakuuttaa heidät siitä, että GeoGebran antamat pinta-alat ovat likiarvoja ja heidän pitäisi tarkistaa pinta-alat myös laskemalla.
Kiinnitimme myös huomiota yhteistoiminnan opettamiseen. Työn alussa selvitimme opiskelijoille, mitä työssä olisi tarkoitus oppia ja millaiset toimintatavat ovat ryhmätyössä toimivia. Kierrellessämme auttamassa ryhmiä kyselimme ryhmän toiminnan sujumisesta ja pyrimme osallistamaan kaikkia jäseniä keskusteluun. Lopussa kaikki ryhmäläiset arvioivat oman ryhmänsä toimivuutta kirjallisesti opettajille (kuva 3). Tällä tavoin kiinnitimme huomiota yhteistyön sujuvuuteen ja teimme näkyväksi, että ryhmä voi vaikuttaa omaan toimintaansa.

Tärkeä osa yhteistyön vahvistamista olivat ryhmätyön roolit. Opiskelijoiden piti aina ryhmätyöskentelyä aloittaessaan valita kullekin ryhmäläiselle rooli, ja näitä rooleja vaihdettiin aina oppituntien välillä. Roolit olivat kirjuri, äänitorvi, kriitikko, osaamisen varmistaja ja ideoija/työnjohtaja. Roolien tavoitteena oli luoda työskentelylle struktuuria, antaa mallia tehtävien jakamisesta sekä antaa opiskelijoille mahdollisuus kokeilla erilaisia tapoja toimia ryhmän jäsenenä.
Ryhmätyöt lisäsivät vuorovaikutusta ja mahdollistivat haastavien tehtävien käytön
Ryhmätyöt lunastivat odotuksemme matemaattisen keskustelun lisääntymisestä. Olimme jopa yllättyneitä siitä, miten laadukkaita matemaattisia ajatuksia ryhmissä vaihdettiin. Ryhmät olivat kaiken kaikkiaan motivoituneita työskentelemään ja vaikutti siltä, että työskentely parani opintojakson edetessä. Joillakin yksittäisillä opiskelijoilla oli kuitenkin loppuun asti vaikeuksia ilmaista ajatuksiaan ja ryhmät toimivat yhdessä eri tasoisesti. Toiminnan sujuvuuteen vaikuttivat ryhmäläisten matemaattinen lähtötaso sekä se, miten hyvin ryhmäläiset tunsivat toisensa: hyvin eri tasoisilla opiskelijoilla yhteistoiminta ei ollut niin sujuvaa varsinkaan, jos opiskelijat eivät tunteneet toisiaan hyvin ennen ryhmätyön aloittamista. Oli selvästi tärkeää, että ryhmätöitä tehtiin koko opintojakson ajan, jotta opiskelijoilla oli aikaa tutustua menetelmään sekä toisiinsa, ja opettajat ehtivät tukea ryhmätoimintaa riittävästi.
Ohjaava opettaja Piia yllättyi erityisesti siitä, että – toisin kuin olisi voinut luulla – ryhmätyötä sisältävällä opintojaksolla kiireen tunne väheni. Tulkitsimme tämän johtuvan siitä, että ryhmätyöt toivat opintojaksolle pitkäjänteisiä elementtejä, kun normaalisti tunteja ja opettajan työtä rytmitti eri aiheiden ennalta määrätty ja usein liian nopeasti vaihtuva asioiden läpikäynti. Nyt tuntui siltä, että opintojaksolla ei niinkään opiskeltu yksittäisiä teoriapaloja, vaan ”tehtiin geometriaa”. Tämä rauhallisuus säilyi myös niillä tunneilla, joilla ryhmätyötä ei tehty.
Haastattelimme opintojakson jälkeen muutamia opiskelijoita. Nämä opiskelijat olivat kokeneet ryhmätyöskentelyn virkistäväksi vaihteluksi. He pitivät sitä myös hyödyllisenä lisänä matematiikan opiskelussa, sillä ryhmän kanssa toimiessa oppi keskustelemaan matemaattisista ideoista ja perustelemaan niitä. Ryhmätyöskentely mahdollisti myös tavallista haastavampien tehtävien kanssa työskentelyn, sillä yhdessä pystyi löytämään enemmän ratkaisuideoita eikä jäänyt niin helposti jumiin kuin yksin tehdessä. Erityisesti todistaminen koettiin tällaiseksi haastavaksi asiaksi, jota pääsi tehokkaasti harjoittelemaan ryhmätyössä. Lisäksi ryhmätyön osuus opintojakson arvioinnissa vähensi arvioinnin kasautumista loppukokeeseen ja tällä tavalla kevensi opintojakson aiheuttamaa stressiä arviointiviikolla.
Rooleista toimivimmiksi ilmenivät kirjuri ja äänitorvi. Erityisesti äänitorven roolin kierrättäminen mahdollisti kaikille matematiikasta puhumisen harjoittelun. (Äänitorven tehtävänä oli kertoa ryhmän edistymisestä opettajalle.) Haastattelemamme ryhmäläiset kuitenkin totesivat, että kaikki opiskelijat eivät osallistuneet keskusteluun yhtä aktiivisesti. He pitivät harmillisena, jos joku ei osallistunut sen takia, että ei kokenut ymmärtävänsä mistä ryhmässä puhutaan, sillä nimenomaan kysymyksiin vastaamalla ja selittämällä myös omat ajatukset kirkastuivat, perustelut paranivat ja oppiminen oli syvempää.
Tulevaisuus
Kokemuksemme ryhmätöistä kannustavat ehdottomasti lisäämään niitä lukiomatematiikan opetukseen jatkossakin. Opiskelijoiden rooli matemaattisen aiheen käsittelyssä oli ryhmätyöskentelyn ansiosta huomattavasti aktiivisempi ja opiskelijat tuntuivat omistavan matemaattisen osaamisensa voimakkaammin kuin ennen ryhmätyöskentelyä, mikä lisäsi itseluottamusta matematiikan opiskeluun.
Olennaista ryhmätyöskentelyn onnistumisessa on ryhmän jäsenten toimivat roolit. Ne vaativat vielä täsmennystä jatkossa, koska esimerkiksi kriitikko ja osaamisen varmistaja menivät osin päällekkäin ja olivat opiskelijoille haastavampia sisäistää kuin esimerkiksi äänitorven rooli.
Tämän lisäksi keskeistä ryhmätyöskentelyn onnistumisessa ovat tehtävät, joita ryhmätyössä ratkaistaan. Tehtävässä tulee olla eri vaikeustasoja sekä erilaisia matemaattisia näkökulmia, jotta eri tasoiset opiskelijat pääsevät työskentelyyn mukaan. Lisäksi tehtävän tulisi olla sellainen, että siihen on olemassa erilaisia ratkaisutapoja, jotta erilaisista ratkaisutavoista syntyisi keskustelua ja vertailua. Näiden keksiminen ei ole helppoa ja olisi hienoa, jos hyväksi koettuja tehtäviä voitaisiin jakaa opettajien kesken.
Koska aina opintojaksoilla ei ehkä ole mahdollista teettää isoja ryhmätöitä, voi ryhmätyön elementtejä hyödyntää pienemmissäkin opetustuokioissa. Pienryhmiä voi pyytää esimerkiksi etsimään eroja ja yhtäläisyyksiä tekemistään ratkaisuista johonkin kotitehtävään, tai opettaja voi esittää opiskellusta aiheesta jonkin väitteen, johon pienryhmän pitää muodostaa mielipide perusteluineen. Parhaassa tapauksessa ryhmästä löytyy useampia mielipiteitä, joista voidaan vielä luokan kanssa keskustella yhdessä. Myös erilaisten ratkaisutapojen keksimistä tai valmiin ratkaisun lukemista ja mahdollista korjaamista voi tehdä hyvin pienryhmässä. Näissäkin tapauksissa eri rooleja kannattaa pienryhmissä kierrättää, koska se selvästi jäntevöittää tekemistä ja osallistaa jokaisen paremmin työskentelyyn.
Lähteitä
[1] Opetushallitus. (2019). Lukion opetussuunnitelman perusteet 2019 [Päivitetty 17.1.2024]. https://www.oph.fi/fi/tilastot-ja-julkaisut/julkaisut/lukion-opetussuunnitelman-perusteet-2019
[2] Johnson, D. W., Johnson, R. T, &; Smith, K. A. (1998) Active Learning: Cooperation in the College Classroom (2nd ed.). Interaction Book: Edina, MN.
[3] Slavin, R. E. (1995). Co-operative Learning: Theory, Research and Practice. Allyn Bacon. Boston.
[4] Slavin, R. E. (2014). Cooperative Learning and Academic Achievement: Why Does Groupwork Work? Anales de psicología/annals of psychology, 30(3), 785–791.
[5] Gillies, R. M. (2016). Cooperative learning: Review of research and practice. Australian Journal of Teacher Education (Online), 41(3), 39–54.
Tilaa Dimension uutiskirje – saat sähköpostiisi aina kuunvaihteessa koosteen tuoreimmista artikkeleista







