Kansalliset matematiikkakilpailut lukuvuoden 2020-2021 aikana
Katsaus menneeseen
Uuden kilpailukauden kynnyksellä huomaan miettiväni edellisen kilpailukauden toteutusta. Tämä on ihan loogista: jälleen on päätettävä miten alkava kilpailukausi hoidetaan.
Kilpailukausi alkaa epävarmuudessa. On varauduttava esimerkiksi siihen, että kilpailija tai kokonainen koulu voi olla karanteenissa kilpailun aikaan. Toisaalta toivoakin on: ehkä saamme jälleen finaalin, jota ei jouduta toteuttamaan etänä. Näin toki toivoimme viime syksynäkin, mutta nyt rokotusten etenemisen ansiosta toive vaikuttaa suhteellisen realistiselta.
Matematiikassa olimme jo vuosi sitten onnekkaita. Huhtikuussa 2020 oli järjestetty Euroopan tyttöjen matematiikkaolympialaiset virtuaalisina. Niiden järjestelyt olivat loistavat, vaikka siirtymä livekilpailusta virtuaalisiin olympialaisiin oli ollut vauhdikas. Hollantilaiset osasivat asiansa. Tämä kilpailu antoi paitsi uskoa, että tarpeen tullessa etäkilpailu onnistuu kyllä, myös mallin sille miten kaiken voi hoitaa.
Alkukilpailut
Kansalliset alkukilpailut järjestettiin syksyllä 2020 omissa kouluissa perinteiseen tapaan. Tehtäväsarjojen rakenne oli vanha ja tuttu: Perussarjassa oli 6 tehtävää, joissa piti valita oikeat vaihtoehdot ja kaksi avointa tehtävää, välisarjassa tehtävätyyppien jako oli 3-3 ja avoimessa sarjassa oli neljä avointa tehtävää. Avoimella tehtävällä tarkoitetaan tässä perinteistä kilpailutehtävää, jossa pyydetään täydellinen ratkaisu.
Välisarjassa oli esimerkiksi seuraava tehtävä:
Tehtävä. Kuvan ympyrän halkaisijalle piirretään kaksi puoliympyrää. Määritä jänteiden pituuksien $a$ ja $b$ funktiona se pinta-ala, joka jää jäljelle, kun puoliympyrät leikataan kuviosta pois. Jänteet ovat yhdensuuntaisia halkaisijan kanssa. Voidaan olettaa tunnetuksi, että puoliympyrät eivät leikkaa toisiaan eivätkä ole päällekkäin.
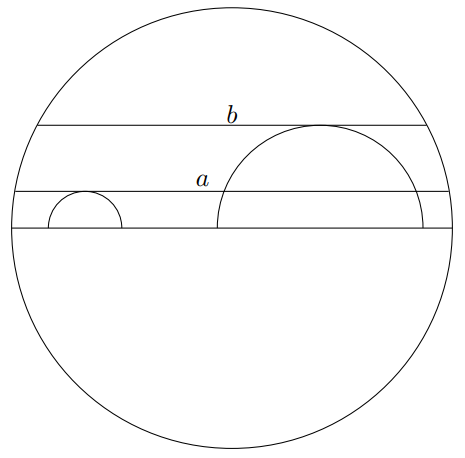
Ratkaisu. Siirretään toinen puoliympyrä ympyrän alapuolelle, toinen pysyy yläpuoliskossa. Siirretään lisäksi molempien puoliympyröiden keskipisteet ison ympyrän keskipisteeseen:
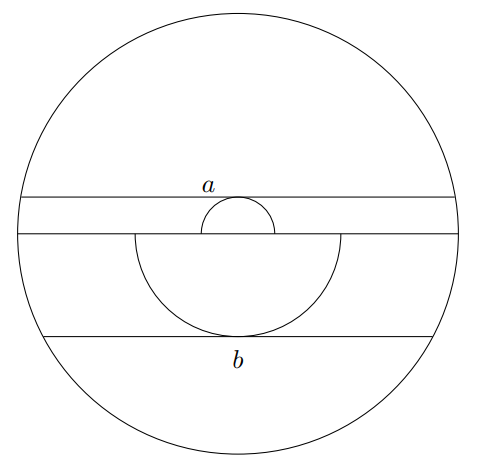
Oletetaan, että ison ympyrän säde on $r$. Tällöin ison ympyrän ala on $\pi r^2$. Tarkastellaan puoliympyrää, joka sivuaa jännettä, jonka pituus on $a$. Piirretään jana ison ympyrän keskipisteestä tämän jänteen ja ison ympyrän kaaren leikkauspisteeseen. Pikkupuoliympyrän säteen neliöksi saadaan näin $r^2-\frac{a^2}{2^2}$. Tämän puoliympyrän ala on siis $\frac{\pi}{2}\left(r^2-\frac{a^2}{2^2}\right)$. Vastaavasti toisen puoliympyrän ala on $\frac{\pi}{2}\left(r^2-\frac{b^2}{2^2}\right)$. Yhteensä jäljelle jäänyt ala on siis $\frac{\pi}{8}(a^2+b^2)$.
Loppukilpailut
Alkukilpailun parhaat kutsuttiin perinteiden mukaisesti loppukilpailuun. Loppukilpailu on tärkeä, sillä siinä missä alkukilpailussa täytyy tehtävät skaalata niin, että mahdollisimman moni lukiolainen saa onnistumisen elämyksiä ja toisaalta saadaan parhaimmisto selville, on loppukilpailun tavoite erilainen: löytää parhaat parhaista niin, että järjestys ei ratkea esimerkiksi pikkuriikkisellä huolimattomuusvirheellä tai huolimattomalla argumentaatiolla yksittäisessä kohdassa. Mikään kilpailu ei tietenkään ole aukoton: toisilla osuu parempi päivä kohdalle, toisilla huonompi, joskus huolimattomuusvirhe taas osuu todella huonoon kohtaan ja vie paljon pisteitä. Päämäärä on kuitenkin selvä. Vaativilla tehtävillä pyritään ratkaisemaan kilpailun voittaja.
Finaalissa oli esimerkiksi seuraava tehtävä:
Tehtävä. Polynomilla $P(x)=x^3+8x-9$ on kolme eri nollakohtaa $\alpha$, $\beta$ ja $\gamma$. Määritellään lisäksi
\[Q(x)=x^7+9\,x^5-9\,x^4+9\,x^3-9\,x^2+9x-8.\]
Mitä on tällöin
\[Q(\alpha)\,Q(\beta)+Q(\beta)\,Q(\gamma)+Q(\gamma)\,Q(\alpha)?\]
Finaalin voitti Daniel Arone. Toisen sijan jakoivat Sampo Siitonen ja Ruby Sun.
Finaali oli ollut tarkoitus järjestää Helsingin yliopiston Kumpulan kampuksella. Tämä ei kuitenkaan ollut talven koronatilanteessa mahdollista. Finaali jouduttiin järjestämään etätapahtumassa. Järjestelyissä jouduttiin pyytämään apua opettajilta, jotta kilpailu saatiin valvottua omissa kouluissa. Kilpailutyöryhmän näkökulmasta kaikki toimi loistavasti. Opettajat valvoivat kilpailut, skannasivat vastaukset, ja kaikin mahdollisin tavoin mahdollistivat kilpailun järjestämisen. Siitä suuri kiitos!







