Korkeakouluvalinnat ja matematiikan ylioppilaskokeen antamat pisteet
Mahdollisuus kirjoittaa sekä pitkä että lyhyt matematiikka ylioppilaskirjoituksissa herättää toisinaan kysymyksen: onko tämä järkevää? Onko merkittävää hyötyä siitä, että oletettavasti pitkän matematiikan lukija kirjoittaa sekä pitkän että lyhyen matematiikan? Opettajien keskuudessa tämä on myös herättänyt huolta: miten käy lyhyen matematiikan pisterajoille ja ketkä keräävät lyhyen matematiikan laudaturit, jos pitkän matematiikan kirjoittajat tulevat kirjoittamaan lyhyttä matematiikkaa.
Tämän tekstin tarkoituksena on esimerkkien avulla valottaa, miksi tällaisesta toiminnasta ei kirjoittajalle luultavasti ole mainittavaa hyötyä, vaan lähinnä saa kuormitettua itseään keräämällä useampia kokeita kirjoitettaviksi.
Ensimmäinen huomioitava asia on se, että lukion pitkä ja lyhyt oppimäärä eivät ole saman oppimäärän järeä versio ja light versio (kuten joskus tunnutaan ajattelevan), vaan kyseessä on kaksi eri oppimäärää omine painotuksineen. Lähtökohtaisesti jo eri oppimäärän opiskelu antaa heikomman lähtötilanteen kirjoituksiin.
Tarkastellaan seuraavaksi tilannetta muutaman esimerkin kautta. Näissä on käytetty kevään 2021 kokeita, pisterajoja ja tehtäviä.
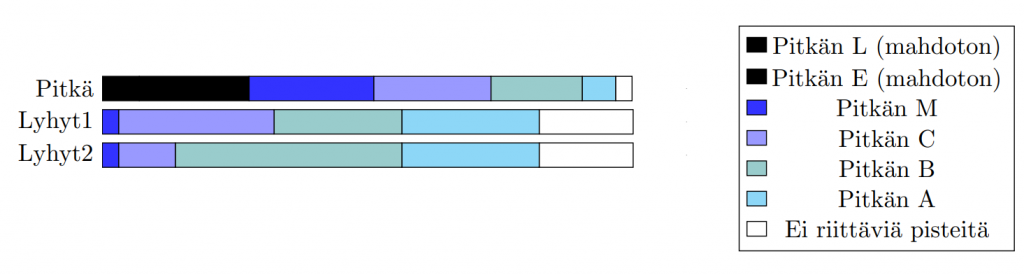
Kokelas A: hakee opiskelemaan hammaslääketiedettä, arvioi saavansa pitkästä matematiikasta vähintään arvosanan M
Lääketieteellisten alojen valinnoissa pitkän matematiikan arvosana M tuottaa 26,4 pistettä. Jotta lyhyestä matematiikasta saisi enemmän pisteitä, pitäisi kirjoittaa laudatur.
Kevään 2021 pitkän matematiikan kokeesta laudaturin sai 7,0
Lyhyen matematiikan laudaturin vuoden 2021 keväällä sai 3,1
Pitkän matematiikan perspektiivi
Pistemäärällisesti pitkän matematiikan magna tarkoitti vähintään 41 pisteen saamista. Tähän riittäisi esimerkiksi se, että olisi saanut ratkaistua oikein tehtävät 1 (Lukujonoja ja funktioita) ja 2 (Vektoreita ja analyyttistä geometriaa), tehtävästä 3 (Murtolausekkeen integraali) olisi saanut varsin hyvin osatut ensimmäiset kaksi kohtaa oikein (yht. 8 pistettä), pahamaineisen tehtävän 4 (Peräaalto) suoraviivaisen ja hyvin osatun toisen kohdan (3 pistettä) ja tämän jälkeen 6 irtopistettä kokeesta. Tämä arvio tietysti edellyttää sitä, että erikseen mainitut tehtävät todella olisi ratkaistu täysin oikein, mikä ei aina toteudu. Toinen puoli asiaa on se, että tyypillisesti kokelas saa paljon enemmän irtopisteitä.
Esitellään selkeyden vuoksi vielä yllämainitut tehtävät:
Tehtävä 1. Tämä tehtävä oli monivalinta. Tässä piti ensin kertoa ensimmäisissä kolmessa kohdassa voivatko seuraavat jonot olla aritmeettisia, geometrisia, kumpaakin tai ei kumpaakaan:
1. $(1, 2, 4, 7,\dots)$
2. $(32, 16, 8, 4,\dots )$
3. $(7, 9, 11, 13,\dots)$
Seuraavat kaksi kohtaa keskittyivät peruslaskutoimituksiin. Vastaukset olivat monivalintoina.
4. Olkoon $f(x)=(2-x)^2$. Silloin funktion arvo $f(-1)$ on
5. Olkoon $f(x)=2x^2-x$. Silloin funktion derivaatan arvo $f'(1)$ on
Viimeisenä alakohtana oli valita monivalintalaatikosta, mitä funktion derivaatan arvo kertoo.
Tehtävä 2. Olkoon $\overline{u} = 5\overline{i}+ 12\overline{j}$. Määritä vektorin
1. $\overline{u}$ pituus.
2. Määritä vektorin $\overline{u}$ kanssa vastakkaissuuntainen vektori, jonka pituus on $5$.
3. $L$ kulkee pisteiden $A = ( 4 , 4 )$ ja $B = (-1 ,-8 )$ kautta. Ovatko suora $L$ ja vektori $\overline{u}$ yhdensuuntaisia?
4. Määritä suoran $L$ yhtälö muodossa $y=kx+b$.
Tehtävä 3. Tämän tehtävän kolmas kohta osoittautui haastavaksi. Sen sijaan ensimmäisistä kahdesta kohdasta sai melko helposti kahdeksan pistettä:
1. Osoita, että yhtälö $$\frac{4}{4-x^2}=\frac{1}{2+x}+\frac{1}{2-x}.$$
on voimassa kaikilla $x\ne \pm 2$.
2. Laske integraali $$\int_{-1}^1\frac{1}{2+x}\,dx.$$
Tehtävä 4. Tämä tehtävä oli kaiken kaikkiaan haastava. Tässä oli kuitenkin helppo toinen kohta, jonka pystyi ratkaisemaan, vaikka ensimmäisessä kohdassa ei olisikaan edistynyt. Toisessa kohdassa on viite ensimmäiseen kohtaan, mutta kyse on vain lukuarvosta, joka oli annettu ensimmäisen kohdan tehtävänannossa. Tämän kohdan osasikin moni sellainen, joka ei ollut ensimmäistä kohtaa ratkaissut. Toisesta oli saatavissa kolme pistettä ja tehtävänanto oli seuraavanlainen:
Veden pinnalla vakionopeudella liikkuvan kappaleen (kuten veneen tai sorsan) taakse muodostuu V-kirjaimen muotoinen peräaalto, jonka avautumiskulma ei tietyillä oletuksilla riipu kappaleen nopeudesta. Kelvinin aaltoteorian mukaan tälle kulmalle $\alpha$ on voimassa yhtälö $$\tan \frac{\alpha}{2} = M ,$$ jossa $M$ on kohdassa 1 laskettu arvo. Määritä kulman $\alpha \in [ 0^{\circ} , 180^{\circ} ]$ likiarvo asteen tarkkuudella.
Koska ensimmäisessä kohdassa oli kerrottu $M=\frac{\sqrt{2}}{4}\approx 0\mathrm{,}3536$, oli kyseessä yksinkertainen sijoitustehtävä.
Lyhyen matematiikan laudaturiin vaadittiin 105 pistettä. Koska maksimipisteet ovat 120, tarkoittaa tämä sitä, että jos yhden tehtävän olisi mokannut täysin, olisi muista tehtävistä pitänyt saada lähes täydet pisteet. Kaiken kaikkiaan suorituksessa ei olisi ollut paljon tilaa virheille.
Kokelas B: hakee opiskelemaan filosofiaa, arvioi saavansa pitkästä matematiikasta vähintään arvosanan B
Filosofian koevalintapisteillä pitkän matematiikan arvosanan B voi voittaa saamalla lyhyestä matematiikasta vähintään arvosanan C.
Pitkässä matematiikassa keväällä 2021 arvosanan B pisteraja oli 20 pistettä. Tähän siis riittäisi loistavasti ylläannettujen ensimmäisten kahden tehtävän osaaminen ja virheitäkin voisi tehdä. Lisäksi 20 pistettä saisi kasaan esimerkiksi tekemällä ensimmäisen tehtävän oikein, saamalla toisesta tehtävästä varsin helposti saatavat ensimmäiset 6 pistettä ja kolmannesta tehtävästä ensimmäiset neljä pistettä, jolloin pisteraja olisi jo ylitetty. Pisteitä voisi kerätä myös irtopisteinä. Lyhyen matematiikan C puolestaan olisi vaatinut 54 pisteen saalista, eli lähes puolet kokeen pisteistä olisi pitänyt ansaita.
Johtopäätökset
Lyhyen matematiikan kirjoittaminen ei ole pitkän matematiikan kirjoittajalle helppo oikotie parempiin pisteisiin korkeakouluvalinnoissa. Lyhyen matematiikan oppimäärä antaa vähemmän pisteitä. Erot pistemäärien välillä riippuvat aineesta (eli onko käytössä pitkää matematiikkaa korostava pistejärjestelmä vai ei) sekä arvosanaluokista. Joka tapauksessa lyhyessä matematiikassa on aina saatava vähintään yksi arvosana parempi kuin pitkässä matematiikassa, jos halutaan saada paremmat valintapisteet. Aina tämä yksi arvosana ei edes riitä, kuten yllä nähtiin. SYK-laskentatavan vuoksi pitkässä matematiikassa parhaita arvosanoja tulee suhteessa enemmän kuin lyhyessä matematiikassa. Tämä entisestään kääntää tilannetta pitkän matematiikan puolelle. Lisäksi oppimäärät ovat sisällöiltään ja painotuksiltaan erilaisia, jolloin järkevintä on kirjoittaa se oppimäärä, jonka on opiskellut.
Kiitokset kuvasta Peter Hästölle.
Tilaa Dimension uutiskirje – saat sähköpostiisi aina kuunvaihteessa koosteen tuoreimmista artikkeleista