Klassiset matemaattiset temput, osa 1
Nyt alkavassa sarjassani esittelen klassikkotaikatemppuja. Klassikkotaikatempuksi nimeän sellaiset, jotka ovat alkuperältään vanhoja, ehkäpä 1900-luvun alkupuolelta, mutta ovat säilyttäneet kiinnostavuuden siten, että temput ovat pysyneet vuosien varrella monien taikureiden ohjelmistossa ja joihin edelleen palataan uusin versioin taikurilehdissä ja -kirjoissa. Suosion pysyvyys kertoo temppujen käyttökelpoisuudesta ja hyvyydestä. Lisäksi tempun pitää olla tavalla tai toisella matemaattinen.

Taikaneliöt
Taikaneliöllä tarkoitetaan tasasivuista, esimerkiksi 3 X 3 tai 5 X 5 kokoista ruudukkoa, joka on täytetty luvuilla. Viereisessä kuvassa on 3 X 3 kokoinen, pienin mahdollinen taikaneliö. Taikaneliössä jokaisen vaaka- pysty- ja vinorivien lukujen summa (rivisumma) on sama. 3 X 3 kokoisessa taikaneliössä luvut yhdestä yhdeksään voivat olla kahdeksalla eri tavalla siten, että kyseessä on edelleen taikaneliö. Voimme myös ajatella, että kyseessä on saman numerojärjestyksen erilaiset peilaukset ja kierrot.
4 X 4 kokoisista taikaneliöistä voi löytää muitakin neljän luvun paikkoja, joiden summa on sama kuin taikaneliön rivisummat.
Taikaneliöissä yhdistyy salatiede, historia, matematiikka ja taikuus. Taikaneliöt ovat ihmetyttäneet ja hämmästyttäneen ihmisiä satoja, ellei vuosia. Varhaisemmat tarinat taikaneliöistä ovat muutamia tuhansia vuosia vanhoja. Taikaneliöillä on uskottu olevan nimensä mukaisesti taikamaisia ominaisuuksia ja voimia. Taikaneliöitä on käytetty uskonnollisissa menoissa, rituaaleissa, salatieteissä, astrologiassa ja alkemiassa. Henkilökohtaisista luvuista lasketuista taikaneliöistä tehdään tänä päivänäkin koruja.
Täynnä matematiikkaa
Taikaneliöissä on symmetriaa, peilauksia, kaavoja, vastakkaisia lukuja, muistisääntöjä, joukko-oppia, yhteenlaskuja, vähennyslaskuja sekä jakolaskuja jakojäännöksineen, vaakarivejä, pystyrivejä ja vinoviivoja (diagonaaleja, lävistäjiä). Taikurilta taikaneliöt yleensä vaativat päässälaskuja. Taikaneliöitä voidaan käyttää pulmatehtävinä ja yhteenlaskuharjoitteluissa. Matematiikkaa taikaneliöissä on alakouluista yläkouluun ja matematiikkakerhoihin asti. Taikaneliöt mahdollistavat erittäin hyviä taikatemppuja.
Taikurit ja taikaneliöt
Yksinkertaisia taikaneliöitä, pulmatehtävinä tai huvituksina on ollut taikurikirjallisuudessa jo 1500-luvulla. Horacio Galasson kirjassa Giochi di Carte Bellissimi di Regola, e di Memoria (1593) on temppu, jossa katsoja haastetaan järjestämään pelikortit ässästä yhdeksään 3 x 3 muotoon siten, että jokaisen rivin korttien summa on 15. 1900-luvun alussa taikaneliöstä oli jo kehitetty taikatemppuja. Taikaneliöitä on piirrelty käyntikorteihin tai suuriin tauluihin. Taikaneliöitä on rakennettu luvuilla, tulitikuilla, dominonappuloilla ja pelikorteilla. Taikaneliöistä on tehty pulmatehtäviä. Niitä on käytetty ajatustenlukemiseen, ennustamiseen ja muistidemonstraatioihin. Taikaneliö on ollut tempun metodina niin, ettei katsoja huomaa sen käyttöä. Taikaneliöitä on piirrelty ja laskettu avoimesti, silmänräpäyksessä katsojan antaman summaluvun mukaan tai taikaneliön pienimmän luvun mukaan tai katsojan numerovalintoja täydentäen. Samoja ideoita on pyöritetty ja muokattu edestakaisin. Kaikki yllä oleva puoltaa sitä, että Taikaneliö sopii erittäin hyvin aloittamaan sarjani Klassista matemaattisista taikatempuista.
Ehdin jo tammikuussa päättää, että en aloita tätä sarjaa taikaneliöllä siksi, että uusimmassa kirjassani Pakottavia Taulukoita ja Paradoksipapereita (MFKA, 2022) on kolmekymmentä kolmen sivuinen luku taikaneliöstä. Tuon päätöksen jälkeen tuli YO-kirjoitusten pitkän matematiikan koe ja siellä taikaneliötehtävä. Jopa Helsingin Sanomat uutisoivat asiaa. Taikaneliötehtävän pohjana oli Albrecht Dürerin maalauksessa Melankolia I näkyvä taikaneliö. Taikaneliön jokaisen vaakarivin ja pystyrivin ja lävistäjien, sekä niin kutsuttujen pikkuneliöiden summa on 34. Alimman vaakarivin keskimmäiset luvut ovat 15 ja 14. Kuva on tehty vuonna 1514. Alla osasuurennos Albrecht Dürerin maalauksessa Melankolia I.

Taulusta on maininta myös kirjassani. Mainittakoon lisäksi, että pitkässä matematiikassa heitettiin noppaa ja lyhyessä matematiikassa sekä noppaa, että kolikkoa! Kummastakin on tarkemmin juttuja kirjassani Syntymäpäiväparadoksi (MFKA 2020). Vaikuttaa siltä, että kirjani ovat hyviä teoksia valmentautumisessa ylioppilaskirjoituksiin. Uusimassa kirjassani Pakottavia Taulukoita ja Paradoksipapereita on taikaneliön historian ja matemaattisen rakenteen analysoinnin lisäksi kuusi taikatemppua, yksi pulmatehtävä ja ohjeet 5 x 5 taikaneliön tekemiseen, kun katsoja määrittelee aloitusluvun ja ruudun, johon tämä luku sijoitetaan. Seuraavassa on samaan sarjaan kelpaava seitsemäs taikaneilötaikatemppu.
Valitut kortit löytävät katsojan pelikortin
Temppu
Taikuri pyytää katsojaa valitsemaan korttipakasta yhden kortin. Kun kortti on katsottu ja näytetty kaikille muille, mutta ei taikurille, taikuri pyytää katsojaa palauttamaan ”tähän saman paikkaan kuin mistä kortin otit”. Muutaman vaihtoehdon ja valinnan jälkeen katsoja on päätynyt kolmeen korttiin, jotka käännetään kuvapuoli ylöspäin pöydälle. Näiden kolmen kortin summa johdattaa korttipakassa katsojan valitseman korttipakan luokse.
Tempun tarkempi kuvaus ja selitys
Ennen temppua järjestät pakan päälle yhdeksän korttia järjestykseen 6, 1, 8, 7, 5, 3, 2, 9, ja 4 sekä toiset yhdeksän korttia samaiseen järjestykseen. Korttien maa-arvoilla ei ole merkitystä, ainoastaan numeroarvoilla. On jopa hyväksi, jos kortit ovat sekaisin eri korttimaita. Jos katsot tuonne ylös, niin huomaat, että järjestys on sama kuin 3 X 3 kokoisessa taikaneliössä. Voit käyttää mitä tahansa 3 X 3 taikaneliön numerojärjestystä ja jopa niin, että ensimmäiset yhdeksän korttia ovat eri taikanelijärjestyksessä kuin yhdeksän seuraavaa pelikorttia. Laita järjestetty pakka korttikoteloon odottamaan esitystä.
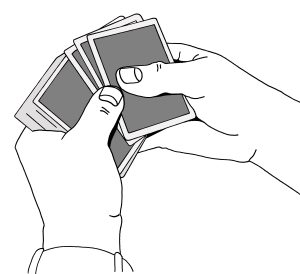
Esityksessä otat korttipakan kotelosta ja tarvittaessa voit esitellä pakkaa kuvapuoli ylöspäin, jolloin katsojat näkevät, että kortit ovat sekaisin. Jos hallitset taidon, voit tehdä valesekoituksen, joka ei muuta pakan 18 kortin järjestystä. Tämä ei kuitenkaan ole tempun uskottavuuden kannalta tarpeellista.
Käännä kortit kuvapuoli ylöspäin. Siirrä vasemman käden peukalolla kahdeksantoista pelikorttia oikean käden peukalon alle. Tämä kannattaa tehdä niin, että siirrät aina kolme korttia kerrallaan, jolloin korttien laittaminen peukalon alle ei näytä laskemiselta vaan ainoastaan korttien siirtämiseltä. Jos kahdeksantoista kortin siirtäminen tuntuu suurelta urakalta, kerron tämän jutun loppupuolella toisen tavan hoitaa sama asia.
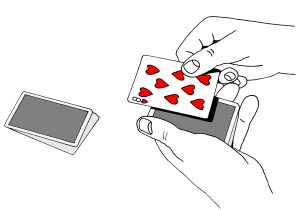
Kun sinulla on kahdeksantoista korttia oikean kätesi peukalon alla, levitä seuraavia kortteja samalla kun ojennat pakkaa katsojan päin ja pyydät katsojaa valitsemaan minkä tahansa kortin. Tämä tarkoittaa, että minkä tahansa kortin, kunhan katsoja ei lähde kaivamaan oikean kätesi peukalon alla olevia kortteja. Vaikka kovin monissa kuvissa valinta ei näy kuvapuoli ylöspäin, esimerkissämme katsojan valinta on herttakahdeksan.
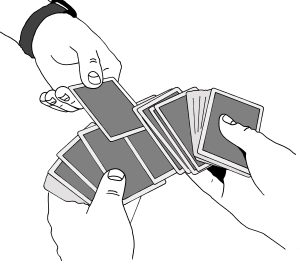
Kun katsoja tutkii valitsemaansa korttia ja näyttää sitä muille, kasaat levitetyt kortit vasempaan käteen. Oikeassa kädessä olevat kortit pidät edelleen oikeassa kädessäsi. Ojennat vasemmassa kädessäsi olevia kortteja kohti katsojaa ja pyydät häntä laittamaan kortin tähän samaan paikkaan, mistä otitkin sen. Todellisuudessa kortti ei tule samaan paikkaan mistä se otettiin, mutta tähän ei kukaan kiinnitä huomiota. Kun katsoja on laittanut kortin vasemmassa kädessäsi olevien korttien päälle, laitat oikeassa kädessä olevat kortit vasemmassa kädessäsi olevien korttien päälle. Katsojan valitsema kortti on nyt pakan päältä laskettuna yhdeksästoista pelikortti.
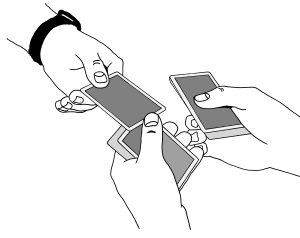
Laske pöydälle kaksi korttipinoa, ensiksi yhdeksän korttia ja sitten toiset yhdeksän korttia. Esityksen kannalta olisi hyvä, jos katsojille syntyisi mielikuva siitä, että et erityisemmin laske korttien määrää, vaan yksinkertaisesti siirrät kaksi pientä korttipinoa pakan päältä pöydälle. Suosittelen esimerkiksi siirtämään kolme korttia kerrallaan oikean käden peukalon alle ja kun oikeassa kädessäsi on yhdeksän korttia, viet pinon pöydälle. Teet samalla tavalla toisenkin pinon pöydälle. Pinojen ottamisen jälkeen vasemmassa kädessäsi olevien korttien päällimmäinen pelikortti on katsojan äsken valitsema kortti.

Pyydä katsojaa valitsemaan toinen pöydällä olevista korttipinoista. Kun katsoja osoittaa pinoa, kysy haluaako hän, että osoitettu pino jää pöydälle vai haluaako hän, että pino nostetaan vasemmassa kädessäsi olevaan pakkaan. Katsojan valinnan mukaisesti nostat toisen pakan vasemmassa kädessäsi olevien korttien päälle. Katsojan valitseman kortin päällä on nyt yhdeksän pelikorttia ja pöydällä on toinen yhdeksän kortin pino.
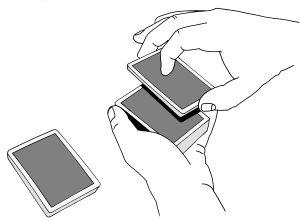
Laske vasemmasta kädestäsi korttipakka pöydälle ja ota pöydältä yhdeksän kortin pino käteesi. Jaa nämä kortit vaakarivittäin pöydälle 3 X 3 järjestykseen. Pyydä katsojaa valitsemaan mikä tahansa ruudukon vaakarivi, pystyrivi tai kolmen kortin vinorivi. Yhdeksällä pelikortilla tehtävä taikaneliö on siitä mukava, että vaikka olisi jakanut kortit pöydälle ja samalla kääntänyt niiden järjestyksen, tulee korteista silti toimiva taikaneliö, kun ne jaetaan vaakarivi kerrallaan pöydälle. Korttien järjestys peilautuu keskimmäisen (5) kortin ympärillä ja muiden korttien järjestys muuttuu, mutta taikaneliömäisyys säilyy.
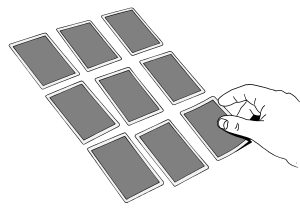
Jos haluat säilyttää tempun salaisuuden koko esityksen ajan, älä mainitse taikaneliötä, kun kortit ovat pöydällä. Joku saattaa tietää, että 3 X 3 taikaneliössä rivin valinnalla ei ole merkitystä, koska kaikkien mahdollisten rivien summa on aina sama. Katsoja tekee valintansa ja kääntää rivinsä kortit kuvapuoli ylöspäin.
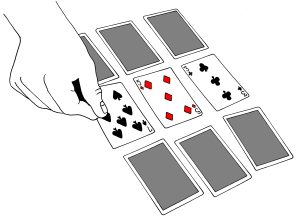
Keräät ne kuusi korttia, jotka jäivät pöydälle kuvapuoli alaspäin, ja nostat ne pöydällä olevan loppupakan päälle. Näiden kuuden kortin jälkeen katsojan valitsema pelikortti on pakan viidestoista pelikortti. Aiemmin nostit katsojan valitseman pelikortin päälle ensiksi yhdeksän kortin pinon ja nyt kuusi korttia.

Katsojan kääntämät korttien arvot lasketaan yhteen. Esimerkissämme 7 + 3 + 3 = 15. Koska pöydälle jaettujen korttien pohjana on 3 X 3 taikaneliö, jokainen valintamahdollisuus tuottaa laskutoimituksen, jonka summaksi tulee 15. Nyt onkin jo helppo nähdä, miten temppu loppuu. Katsojan tempun alussa valitsema pelikortti (Herttakahdeksan) on pakassa viidentenätoista korttina. Laskutoimituksen summa on 15. Otat pöydältä pakan. Muistuta vielä katsojia siitä, että katsojan kääntämien korttien arvojen summa on viisitoista. Jaat pakasta kortteja pöydälle yhteen pinoon ääneen laskien. Et jaa viidennettätoista korttia. Pidät sen kädessäsi kuvapuoli alaspäin ja kysyt katsojilta, että minkä kortin katsoja tempun alussa valitsi. Saat vastauksesi herttakahdeksan. Käännät viidennetoista kortin kuvapuoli ylöspäin ja se on kuin onkin – katsojan tempun alussa valitsema kortti herttakahdeksan!
Onko kahdeksantoista korttia liikaa?
Jos tempun alussa tapahtuva korttien siirto oikean käden peukalon alle tuntuu hankalalta korttien määrän vuoksi, voit aloittaa tempun pudottamalla yhdeksän korttia pöydälle yhdeksi pinoksi. Tämä kannattaa tehdä niin, että otat pakan päältä kolme korttia ja viet ne yhtenä nippuna pöydälle. Toista tämä vielä kaksi kertaa, kunnes pöydällä on yhdeksän pelikorttia.
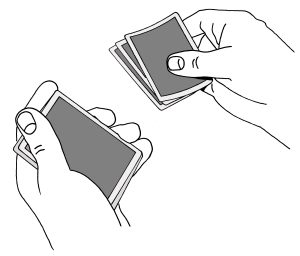
Samalla kun suoristat nämä kortit yhdeksi pinoksi, toteat katsojalle hämmentyneenä, että ”Hetkinen, sinun pitää ensiksi valita yksi pelikortti”.
Etenet kuten ensiksi ehdotin: selaat kortteja pakan päältä oikean käden peukalon alle. Tämä on nyt nopeampaa ja helpompaa, koska työnnät vain yhdeksän korttia pakan päältä oikean käden peukalon alle. Muutoin temppu jatkuu tästä lähes kuin edellä. Sinulla on jo yksi yhdeksän kortin pino pöydällä, joten kohta jaat pöydälle vain toisen samankokoisen katsojan valittavaksi.
Historiaa
Kun keräsin temppuja viimeisimpään kirjaani Pakottavia Taulukoita ja paradoksipapereita (MFKA, 2022), löysin kolme korttitemppua, joissa jokaisessa käytettiin taikaneliötä siten, että katsojalle ei mainosteta tempun taustalla olevaa taikaneliötä. Löydöksistäni kaksi päätyi kirjaani saakka (Taikaneliö vie perille, sivut 68–70 ja Kaksikymmentäneljä, sivut 83–85). Kolmas temppu vaati enemmän muokkauksia, jotta se soveltuisi paremmin henkilöille, jotka eivät käsittele pelikortteja edes viikoittain. Jätin sen kirjasta pois, mutta julkaisin sen nyt vahvasti muokattuna tässä artikkelissa. Temppua ei ole aiemmin Suomessa julkaistu. Alkuperäisen tempun on aikoinaan antanut Hugard’s Magic Monthly —lehden helmikuun numeroon vuonna 1945 (VOL II, Number 9) amerikkalainen pörssimeklari ja temppujen harrastaja ja julkaisija Royal Van Heath.
Martti Sirén on hämeenlinnalainen taikuri, tietokirjailija, työpajakouluttaja, taikuuden historian penkoja ja myös ylioppilaskirjoituksissa käytettyjen tarinoiden kertoja. Sirén on kirjoittanut neljä kirjaa matemaattisista taikatempuista, ja pitänyt matemaattisten taikatemppujen työpajoja opettajille yli viidentoista vuoden ajan.
Edellinen taikuriartikkeli: Matemaattisia taikoja ja variaatioita muistilehtiöistäni, osa 6: Pelikorttien matematiikka (4.4.2023)
Tilaa Dimension uutiskirje – saat sähköpostiisi aina kuunvaihteessa koosteen tuoreimmista artikkeleista







