Spirografi

Spirografi (spirograph) on geometrinen piirustuslaite, joka löytyy monesta vähänkään isommasta marketista askartelu- tai leluhyllystä aika edulliseen hintaan. Spirographin idea on se, että ulompi ympyrän muotoinen kehikko, jossa on hammasrattaat, kiinnitetään mukana tulevalla kitillä paperiin ja toinen ympyrän muotoinen ratas laitetaan tämän kehikon sisälle tai ulkopuolelle. Ympyrän muotoisessa rattaassa on reikiä eri säteen etäisyydellä ympyrän keskipisteestä, josta voi laittaa kynän läpi. Kun sisempi, ympyrän muotoinen ratas pyörii ulomman kehikon ympäri, niin kynä muodostaa liikkuessaan suljetun itseään leikkaavan viivan. Tätä syntynyttä kuviota nimitetään hypotrokoidiksi. Kuvion muoto riippuu sisemmän ympyrän ja ulomman kehikon rattaiden suhteesta, sekä kynän paikasta sisemmällä rattaalla. [1]

Vuonna 1827 englantilainen arkkitehti ja insinööri Peter Hubert Desvignes kehitti ja mainosti ”Speiragraphia” laitteena, jolla voitiin piirtää monimutkaisia spiraalipiirustuksia. Eri henkilöt hänen jälkeensä ovat kehitelleet laitetta edelleen. Spirografi on ollut leluhyllyssä myytävänä ensimmäisen kerran 1965, jonka kehitti brittiläinen insinööri Denys Fisher ja niinpä tätä laitetta myytiin hänen omalla tuotemerkillä oman firman kautta. Sprirografi laitteen myyntioikeudet leluvalmistaja Hasbro Inc:in on ostanut Danys Fisheriltä vuonna 1998. Kaupassa myytävän laitteen valmistaja maksaa lisenssimaksut Hasbrolle.

Voisiko tietokoneen laittaa piirtämään hypotrokoidista kuviota kuten kaksi hammasrattailla varustettua kiekkoa? Se on itse asiassa helppo toteuttaa ohjelmointikielellä, jossa mukana on xy-koordinaatisto. Sellainen löytyy esimerkiksi Scratchissä, mutta Scratch on huono valinta tähän tarkoitukseen, koska Scratch:ssä kulmat muuttuvat välillä 0°…180° ja –180°…0°, joka tekee piirtämisestä hieman hankalampaa. Joten valitsemme ohjelmointikieleksi P5js-ohjelmointikielen, jossa kulmat kasvavat asteikolla 0°…360°. Lisäksi tarvitsemme laskukaavan, kuinka xy-koordinaatit lasketaan sisemmässä ympyrässä. Nämä laskukaavat ovat muotoa:

$$x=R[(1-k)\cdot \cos \theta+L\cdot k\cdot \cos \frac{1-k}{k}\cdot \theta ]$$

$$y=R[(1-k)\cdot \sin \theta – L\cdot k\cdot \sin \frac{1-k}{k}\cdot \theta ]$$

missä

$R$ = ympyrän säde

$k$ = rattaiden hammasten suhde = $\frac{sisempi ratas}{ulompi ratas}$,

$L$ = kynän paikka rattaassa, 0 < $L$ < 1.

$\theta$ = kulma, 0 ≤ $\theta$ ≤ 360. [1]

Tehdään tämän laskukaavan perusteella P5js-ohjelma, joka näyttää seuraavanlaiselta:

var kulma = 0;    // Alkuarvo, älä muuta (laskuri)
var sade = 300;   // Ympyrän säde
var paikka = 0.5; // Kynän paikka. Saa arvoja 0.1 ... 0.9
var k = 63/105;   // Rattaiden suhde
function setup() {
  createCanvas(602, 602);    // Ikkunan koko
  background(240);           // Taustaväri vaalean harmaa
  angleMode(DEGREES);        // Kulma-asteikko käytössä
  strokeWeight(3);           // Reunaviivan paksuus
  stroke(255,0,0);           // Reunaviivan väri punainen
  ellipse(300,300,600,600);  // Piirrä ympyrä, jonka halkaisija on 600
}

function draw() {
  translate(width/2, height/2);    // Origo-ikkunan keskelle
  rotate(55);                      // Aloituskulma
  kulma++;                         // Kasvata laskuria
  var x = sade*((1-k)*cos(kulma) + paikka*k*cos((1-k)*kulma/k))
  var y = sade*((1-k)*sin(kulma) - paikka*k*sin((1-k)*kulma/k))
  point(x, y);                     // Piirrä pisteitä, joista muodostuu käyrä
}

Katso toimiva esimerkki koodista: https://editor.p5js.org/riekkinen/sketches/vtjWQPiAM

Ohjelmassa kulma on laskurimuuttuja. Laskurimuuttujan arvo kasvaa aina yhdellä, koska draw-lohko on ikuisessa silmukassa. Kun kulma kasvaa jatkuvasti, niin samalla saamme laskettua pisteiden (x, y) uusia arvoja jatkuvasti xy-koordinaatistossa. Piste voidaan piirtää point(x,y); komennolla. Näistä pisteistä muodostuu haluttu kuvio. Kokeile muuttaa paikka ja k muuttujien arvoja, jotka ovat heti ohjelman alussa. Havainnollistetaan vielä ohjelman toimivuutta muutamien esimerkkien avulla.

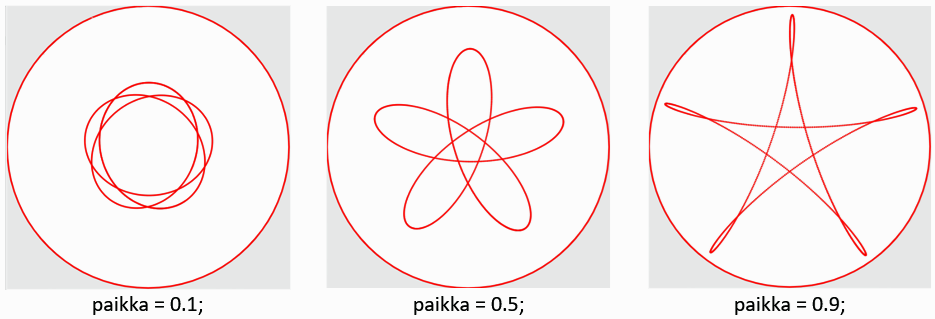
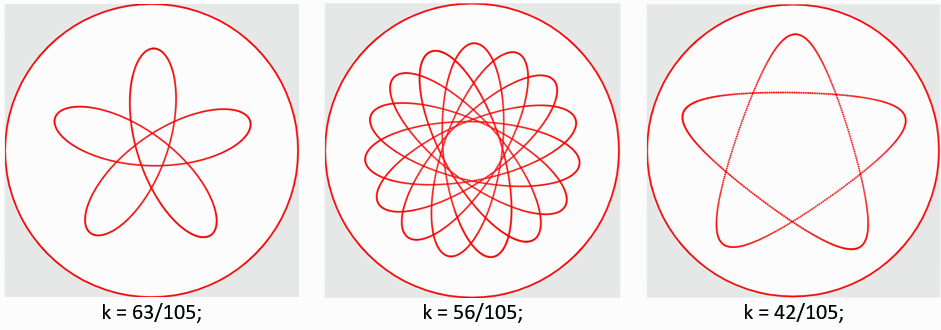
Erilaisten variaatioiden määrä tietokoneella piirrettäessä saadaan paljon suuremmaksi kuin kiekkojen avulla, vaikka sekin on jo suuri. Kokeile muuttaa ohjelmassa kynän paikkaa ja rattaiden suhteita. Internetistä löytyy myös Geogebralla toteutettuja piirtelyohjelmia. Voit kokeilla myös niitä. Hauskoja piirtelyhetkiä!

Lähteet ja lisää lukemista

[1] Wikipedia: Spirograph https://en.wikipedia.org/wiki/Spirograph

Wikipedia: Hypotrochoid https://en.wikipedia.org/wiki/Hypotrochoid

Tilaa Dimension uutiskirje – saat sähköpostiisi aina kuunvaihteessa koosteen tuoreimmista artikkeleista