Amplify Polypad: Yhtälön ratkaisun visualisointia yhtälövaa’an avulla
Amplify Polypad on sähköinen matemaattinen leikkikenttä lähinnä perusasteen matematiikkaan. Ympäristö on täysin ilmainen oppilaille ja opettajille. Ohjelma toimii selainpohjaisesti, mutta ohjelma voidaan asentaa selaimen osoiterivistä myös käynnistymään kuvakkeen avulla itsenäisesti, jolloin käynnistyskuvake saadaan esimerkiksi oppilaan ChromeBookissa käynnistyshyllyyn. Polypad-ohjelma sisältää monipuolisen kattauksen erilaisia matemaattisia työkaluja ja geometrisia piirustustyökaluja. Ohjelmalla voidaan havainnollistaa erilaisia matemaattisia ilmiöitä, kuten esimerkiksi murtoluvut, alkuluvut, lukusuora, xy-koordinaatisto ja diagrammit. Mukana on myös piirtotyökaluja luovaan toimintaan, kuten esimerkiksi monikulmiot, Penrosen laatat, viisikulmiot jne., sekä matemaattisia pelejä, kuten esimerkiksi shakki ja Tangram-palapelit. Myös sähköinen harppi, viivoitin ja kulmaviivoitin löytyvät. Tässä artikkelissa käymme esimerkkien avulla yhtälön ratkaisua yhtälövaa’an ja algebralaattojen avulla käyttäen Polypad-ohjelmaa.
Ohjelman käynnistäminen
- Mene osoitteeseen: https://polypad.amplify.com/
- Paina Launch Polypad -kuvaketta
Yhtälövaaka
Haluamme ratkaista yhtälön 3x – 2 = x + 4 ja havainnollistaa ratkaisua yhtälövaa’an avulla. Kuinka se onnistuu?
- Mene kohtaan Algebra | Balance Scale ja tartu hiirellä yhtälövaakaan ja raahaa se työpöydälle. Näet vaa’an molemmin puolin katkoviivalla merkityn suorakulmion. Näiden suorakulmioiden sisään voidaan nostaa symbolikuvioita (ympyrä, neliö, risti, paino, tähti, sydän), joka kuvastaa tuntematonta muuttujaa. Lisäksi voit kohdasta: Numbers | Number Cards, nostaa erilaisia numerokortteja vaakaan. Tällä kertaa valitsemme kuitenkin algebralaatat.
- Mene kohtaan: Algebra | Algebra Tiles. Raahaa yhtälön vasemmalle puolen katkoviivan sisälle kolme x-laattaa ja kaksi –1-laattaa, sekä raahaa yhtälön oikealle puolen katkoviivan sisälle yksi x-laatta ja neljä 1-laattaa. Olemme nyt luoneet alkutilanteen eli yhtälön: 3x – 2 = x + 4. Lopuksi vaaka pitää tasapainottaa. Napsauta vaan keskelle ja valitse avautuvasta kelluvasta valikosta komento: Balance eli tasapainota.
- Lähdemme ratkaisemaan yhtälöä. Aluksi poistamme yhtälön vasemmalta puolen luvun –2 käänteisillä laskutoimituksilla eli lisäämällä +2. Nostamme kaksi 1-laattaa yhtälön vasemmalle puolen. Heti havaitsemme, että vaaka ei ole enää tasapainossa. Sama luvun lisäys pitää siis tehdä myös yhtälön oikealle puollelle.
- Nostamme kaksi 1-laattaa vaa’an oikealle puolen ja nyt vaaka on tasapainossa.
- Kokeile seuraavaa eli raahaa hiirellä 1-laatta –1-laatan päälle. Tällöin summaksi tulee 0. Sama idea toimii, jos käytät yhtälössä numerokortteja (Numbers | Number Cards). Eli voimme havainnollistaa yhtälön sieventämisen eli luvun ja vastaluvun summan.
- Samalla idealla poistamme yhtälön oikealta puolen x-laatan lisäämällä –x-laatan sekä yhtälön vasemmalle että oikealle puolen.
- Seuraavaksi raahaamme –x-laatan x-laatan päälle, jolloin summaksi tulee 0. Tämän samanmuotoisten termien yhdistämisen teemme sekä yhtälön vasemmalle, että yhtälön oikealle puolen.
- Nyt olemme saaneet yhtälön supistettua muotoon 2x = 6. Jos raahaamme toisen x-laatan pois yhtälön vasemmalta puolen tai painamme Delete-painiketta kelluvasta valikosta, niin silloin puolitamme x-laattojen lukumäärän. Nyt yhtälö menee epätasapainoon, joten sama laskutoimitus pitää tehdä myös yhtälön oikealle puolen.
- Joten lopuksi poistamme puolet 1-laatoista yhtälön oikealta puolen. Olemme siis saaneet ratkaistua yhtälön ja yhtälön ratkaisu on x = 3, kuten kuvasta voimme havaita.
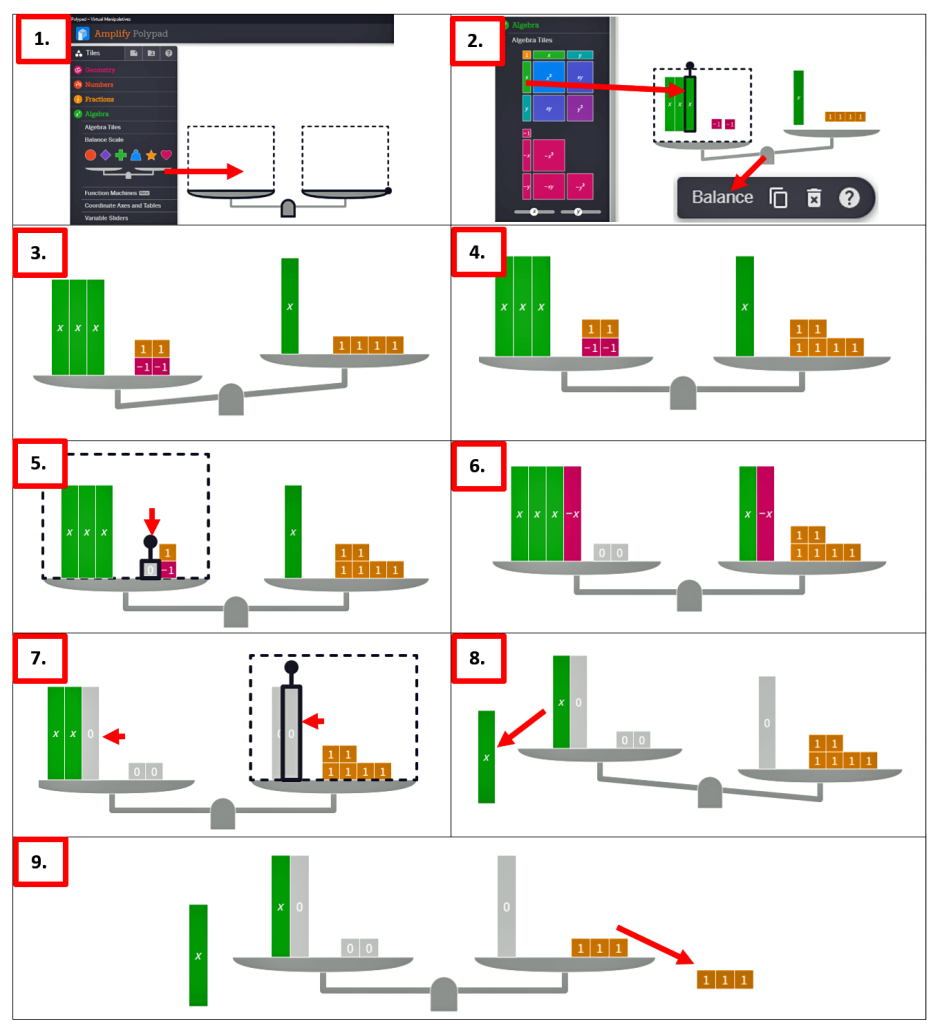
Kun rinnan kuljettaa yhtälön ratkaisun matemaattiset merkinnät, niin tämä antaa nopean tavan havainnollistaa visuaalisesti yhtälön välivaiheita. Työkalua voi käyttää opettajajohtoisesti demonstraatiomielessä, mutta myös oppilaan työkaluna. Tärkeintä on saada oppilaan oma kokeilemalla tehty oivallus ja opettajan perustelu laskun välivaiheista, jotta ohjelman käyttö lisää ymmärrystä yhtälön ratkaisuun. Syvällisesti ymmärtäen opittu ja konkreettisesti itse kokeiltu asia jää paremmin mieleen, kuin ulkoa opettelu ilman oivallusta. Mutta tietysti toistoakin eli laskurutiinia tarvitaan ymmärryksen ja muistin tueksi. Yhtälövaaka-työkalusta olisi varmasti suurta apua esimerkiksi erityisopettajille.
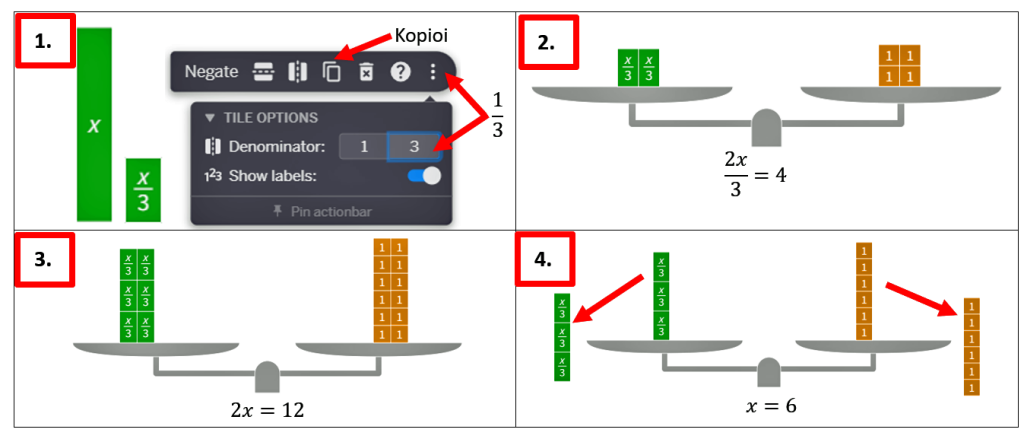
Myös murtoyhtälöitä on helppo havainnollistaa vaa’an avulla.
- Kun nostat x-algebralaatan, niin kelluvasta valikosta katso kohta: Kolme pistettä (More Tools) ja sieltä kohta Denominator (nimittäjä). Muuta toinen Denominator-luvuista 3:seksi, niin saat kolmasosan x-laatasta.
- Voit kokeilla ratkaista yhtälövaa’an avulla esimerkiksi seuraavan murtoyhtälön. Nosta algebralaatat yhtälövaakaan kuten kuvassa.
- Kun tarvitset kolminkertaisen määrän laattoja, niin näppärästi se onnistuu siten, että valitset esimerkiksi hiirellä molemmat x/3 laatat ja painat kaksi kertaa Kopioi-painiketta. Samalla tavalla kopioi myös neljä 1-laattaa.
- Lopuksi puolita sekä yhtälön vasen ja oikea puoli. Kuvasta on helppo havaita, että kolme kolmasosaa on yksi kokonainen, jolloin yhtälön ratkaisu on x = 6.
Yhtälön graafinen ratkaisu
Katsotaan lopuksi vielä, kuinka yhtälön graafinen ratkaisu onnistuu Polypad-ohjelmalla. Ratkaisemme yhtälön 3x – 2 = x + 4 graafisesti. Teemme oman kahden muuttujan yhtälön sekä yhtälön oikeasta, että vasemmasta puolesta ja piirrämme niistä kuvaajat, jolloin yhtälön ratkaisu löytyy näiden kahden suoran leikkauspisteestä.
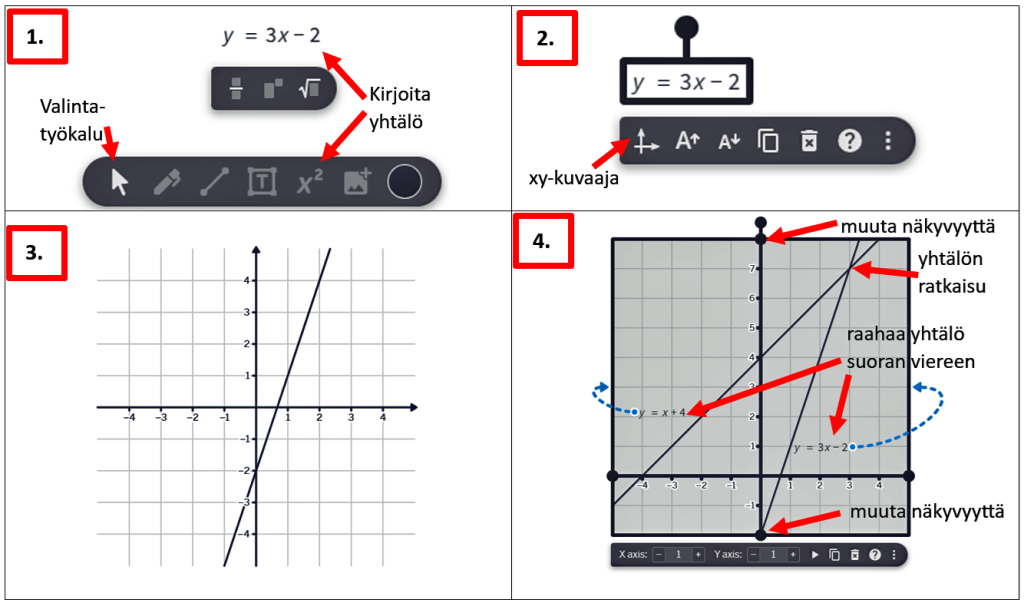
- Valitse ikkunan alareunasta yhtälötyökalu (Equation) ja kirjoita näppäimistöllä yhtälö y = 3x – 2.
Huomio: Tarvittaessa lisää kertomerkki yhtälöön eli tällöin kirjoita tällöin yhtälö muodossa y = 2∙x – 2. Kertomerkin saat näppäimistöltä painamalla * merkkiä. Kertomerkkiä ainakin tarvitaan silloin kun käytät kulmakertoimena jotain kirjainta, joka löytyy liukupalkista (Algebra | Variable Sliders). - Valitse valintatyökalulla (nuoli) juuri kirjoittamasi kahden muuttujan yhtälö ja napsauta xy-kuvaaja (Graph) painiketta avautuvasta kelluvasta työkaluvalikosta.
- Nyt ilmestyy xy-kuvaaja suorasta y = 3x – 2 työpöydälle.
- Toista vaiheet 1 – 3 yhtälölle y = x + 4. Säädä lopuksi x ja y akseleita niin, että saat esille suorien leikkauspisteen. Yhtälön 3x – 2 = x + 4 ratkaisu on siis x = 3, joka nähdään myös kuvaajasta. Myös kirjoittamasi yhtälöt kannattaa raahata xy-kuvaajaan suorien viereen.
Vinkki: Voit lopuksi helposti tallentaa xy-kuvaajan png- tai jpg- kuvaksi Export-painikkeella. Näin oppilas voi palauttaa tekemänsä kuvaajan opettajalle esimerkiksi sähköisessä oppimisympäristössä.

Tehtävien jakaminen oppilaille
Yhtälövaakaa voi myös käyttää tehtävien tarkistamiseen. Kirjoita yhtälötyökalulla (Equation) laskutoimitus ja nosta se yhtälövaa’an vasemmalle puolen. Vastaus voidaan antaa myös kirjoittamalla yhtälötyökalulla, mutta se voi yhtä hyvin numerokortti (number cards), numeropalkki (number bars) tai vaikka pelikortti (playing cards). Vastaus on oikein, kun vaaka on tasapainossa. Kuinka tehtävä voitaisiin jakaa oppilaille?

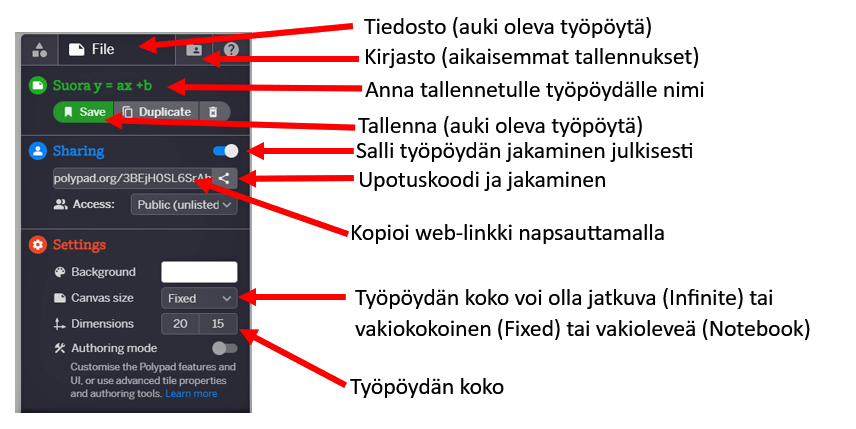
Jos luot oman tunnuksen Polypad-ympäristöön, niin voit tallentaa tekemäsi työpöydän sisällön Polypadin omalle palvelimelle omaan kirjastoosi. Kirjastossa olevia omia tallennettuja työpöytiä voit jakaa myös Internetissä kätevästi web-linkin tai upotuskoodin avulla, jonka saat kohdasta: File | Sharing. Esimerkiksi MAOL2-ympäristö tukee upotuskoodia, jolloin tekemäsi yksittäiset Polypad-työpöydät muodostavat tehtäväkokonaisuuden ja saat ne osaksi kurssin suoritusta. Tämä antaa sähköisen oppimateriaalin tekemiselle uuden vuorovaikutteisen ulottuvuuden. Oppilaat voivat myös palauttaa tehtävät Polypad-ympäristön kautta, jos myös oppilailla on oma tunnus.
Yhteenvetona voidaan todeta, että Amplify Polypad on monipuolinen ja visuaalinen matematiikan työkalu oppitunneille. Työkalua voidaan käyttää demona opettajajohtoisesti tai vuorovaikutteisena tehtävätyökaluna eri oppimisympäristöissä, mutta toisaalta Polypad sopii myös ihan omatoimiseen luovaan matemaattisten ilmiöiden tutkimiseen tai vaikka musiikin ja matemaattisen taiteen tekemiseen. Kaikki pohjat saadaan lisäksi tallennettua omaan kirjastoon myöhäisempää käyttöä varten ja lisäksi ne voidaan linkittää osaksi eri oppimisympäristöjä. Jos kaipaat lisää ohjeita, niin YouTubessa löytyy paljon videoita, kuinka Polypad-ohjelmaa voidaan hyödyntää opetuksessa.