Askartelua ja aivojumppaa: monitahokkaita 1

Kolmiulotteisuus on nykyään opetussuunnitelman perusteiden mukainen geometrian opetuksen lähtökohta. Särmiöt ja kartiot tulevat oppilasta vastaan jo alaluokilla sekä säännölliset monitahokkaat myöhemmin perusopetuksessa tai lukiossa. Monitahokkaita on kuitenkin paljon muitakin kuin niitä, joita oppikirjoissa tavallisesti käsitellään.

Monitahokkaisiin tutustutaan jo perusopetuksen alaluokilla. Esimerkiksi Varga–Neményi-yhdistyksen oppikirjasarjassa ne tulevat esille vähitellen ensimmäisistä kouluvuosista alkaen ja tarkemmin neljännen kouluvuoden keväällä. Yleiskäsitteiden nimiä ”lieriö” ja ”kartio” ei vielä käytetä, vaan puhutaan monikulmioista rakennetuista kappaleista. Yksityiskohtien nimityksiä opetellaan (kuva oppikirjasta [1]). Suorakulmaisia särmiöitä käsitellään tarkemmin. Niitä kootaan sekä irrallisista monikulmioista että pinnan tasolevityksistä. Edelleen rakennellaan suorakulmaisista särmiöistä koostuvia monitahokkaita. Konkreettisuus ja toiminnallisuus ovat vahvasti esillä.

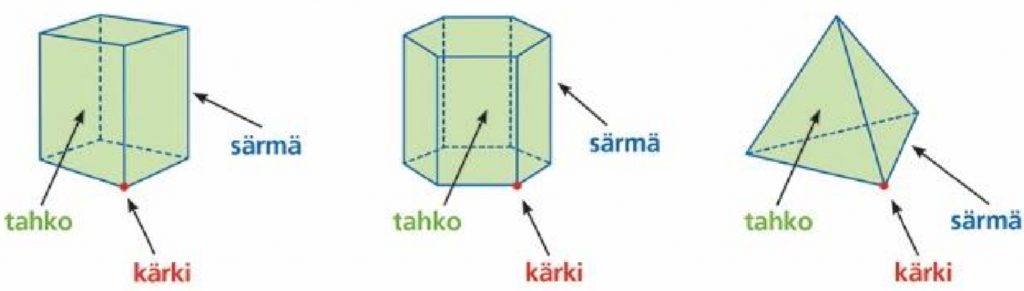
Yläluokkien kirjoissa monitahokkaita käsitellään laskennallisemmin. Esimerkiksi Avoimen oppikirjan [2] yhdeksännen luokan materiaalissa mainitaan luettelonomaisesti sekä Platonin että Arkhimedeen kappaleet. Edellisten pinta-alan ja tilavuuden kaavat esitetään ja niihin liittyviä laskuja harjoitellaan, samoin kappaleiden tasoleikkauksiin liittyviä laskuja. Lukion kirjoissa käsitellään lieriöitä ja kartioita, myös säännölliset monitahokkaat tulevat esille; Geogebra-havainnollistuksia on oppikirjojen lisämateriaaleissa [3].

Kappaleiden rakentaminen on hyvä esimerkki sellaisesta matematiikan tekemisestä, jossa laskeminen ei ole pääosassa. Toiminnallisuudesta matematiikanopetuksessa on hyvä katsaus Essi Nevalan diplomityössä [4], vaikka sen pääaihe kohdistuukin muualle. Monitahokkaiden pintojen aukilevityskuvia on oppikirjoissa ja verkkolähteissä rakentelun lähtökodaksi. Mainioita ohjeita on muuallakin [5] kuin matematiikan oppikirjoissa. Myös aukilevityskuvien (engl. net) piirtäminen voidaan jättää oppilaiden tehtäväksi heti, kun taidot antavat myöten. Silloin kappaleen rakentamisesta muodostuu yksittäisen harjoituksen sijasta kokonainen valmistusprosessi, joka antaa kokemuksen tuloksen tekemisestä alusta loppuun.

Rakentelun pedagoginen merkitys on toiminnallisuudessa itsessään työtapojen monipuolistajana, mutta myös siinä, että se tuottaa merkityksiä luovaa perushahmotusta ennen käsitteiden muodollista määrittelyä ja nimeämistä sekä siirtymistä käsitteellisen tason toimintaan. Tätä oppimisen vaihetta on suomalaisissa opetussuunnitelmateksteissä nimitetty aiemmin aiheeseen tutustumiseksi.

Eikä rakentelun tarvitsisi rajoittua särmiöihin, kartioihin ja säännöllisiin monitahokkaisiin. Esimerkiksi kaksoiskartio (kahdeksantahokas, oktaedri, oikeanpuolimmainen kuva alempana) ei ole paljonkaan vaikeampi rakentaa. Se on muutenkin mielenkiintoinen, sillä se voidaan nähdä myös antiprismasarjan yksinkertaisimpana kappaleena. Antiprismoilla [6] on se sama ominaisuus kuin särmiöilläkin (prismoilla), että niillä on kaksi yhdensuuntaista, yhtenevää pohjaa, jotka ovat säännöllisiä monikulmioita. Sivutahkot ovat keskenään yhteneviä, tasakylkisiä kolmioita. Rakentaminen aukilevityskuvasta ei ole yhtään vaikeampaa kuin särmiöidenkään rakentaminen. Antiprismoja on vältelty koulumatematiikassa ehkä sen takia, että tilavuuden laskeminen edes integroimalla ei ole yhtä yksinkertaista kuin särmiöiden tapauksessa.

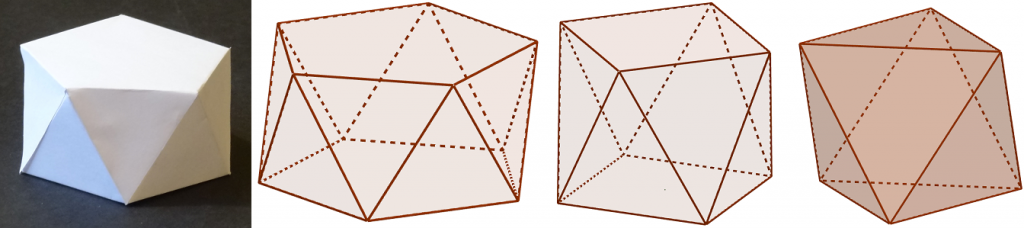
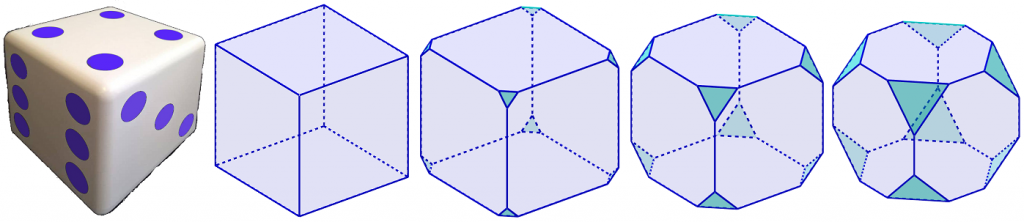
Toinen helposti ymmärrettävä ryhmä monitahokkaita ovat typistetyt (truncated) säännölliset monitahokkaat. Osa niistä on lisäksi suhteellisen helposti rakennettavia. Eivätkä ne ole aina niin outoja kuin matemaattiset nimet saattavat antaa ymmärtää, sillä esimerkiksi tavallinen arpanoppa on hivenen pyöristetty typistetty kuutio.

Konkreettiset mallit ja kappaleiden rakentelu ovat tärkeitä myös siksi, että ”kolmiulotteiset matematiikan tehtävät koetaan oppijoiden toimesta usein vaikeiksi, koska he eivät osaa muodostaa niitä mielessään. Kolmiulotteinen piirtäminen on vaikeaa, eikä siitäkään saa aina oikeaa käsitystä”, niin kuin Miika Suvanto kirjoittaa pro gradu -työssään [7]. Hän tarjoaa ratkaisuvaihtoehdoksi 3D-tulostusta. Tätä päivää se ei vielä ole opetuksen valtavirrassa, sillä 3D-tulostimia ei kouluissa ole. Suunnitteluohjelmien käytön omaksuminenkin muodostaa oman kynnyksensä, sillä siinä on se sama ongelma kuin kaikkien tietovälineiden käytössä, että se vie huomiota ja käytettävissä olevaa aikaa pois varsinaisesta opittavasta asiasta. Mahdollisuudet ovat kuitenkin suuret ja ehkä suunnitteluohjelmistojen kehittyminen muuttaa tilannetta tulevaisuudessa.

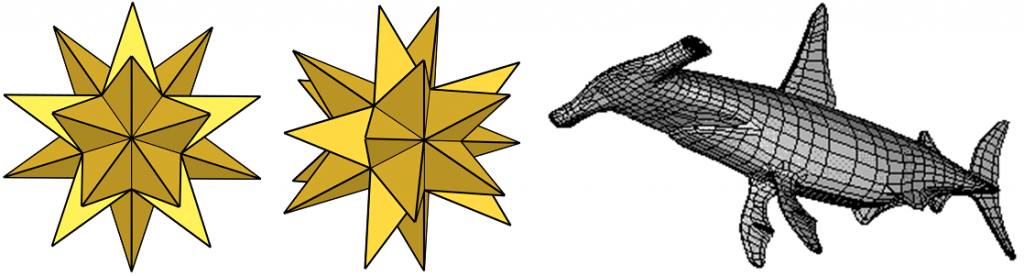
Kaksiulotteiseen kuvaan tuo uuden ulottuvuuden sähköisten kuvien dynaamisuus. Jo kaksiulotteinen geometria tekee mahdolliseksi monitahokkaan pyörittelyn, zoomaamisen ja pinnan levittämisen tasoon. Kaiken tämän tekeminen on kuitenkin paljon helpompaa ja muistuttaa enemmän konkreettisen materiaalin kanssa askartelemista, kun työ tehdään 3D-grafiikan avulla. Tällaiset työvälineet ovat nykyään arkipäivää kaikissa matematiikkaohjelmissa, myös ilmaisessa GeoGebrassa. Dynaaminen kuva ”elää” niin, että kappaleita voi pyöritellä vapaasti ja katsella eri suunnista. Materiaalia on hyvin runsaasti verkossa [8], [9], [10], [11]. Esimerkiksi haulla ”solids geometry” saat 25 000 tulosta. Mitään rajaa monitahokkaiden monimuotoisuudella kun ei ole [12], [13]. Kuvan oikeanpuolimmaisella monitahokkaalla on tuhansia sivutahkoja.

Lähteitä ja lisää lukemista:

[1]   Neményi, E. ym. Matematiikkaa 4b. Varga-Neményi ry, 2019.

[2]   Toivola, M. ja Härkönen, T. Avoin matematiikka 9. lk., osio2 sivulla https://avoinoppikirja.fi/tiedostot/ylakoulu/matematiikka/avoin_matematiikka_9lk_osio2.pdf

[3]   Esimerkit ovat avoimesta materiaalista, sillä usein oppikirjojen lisämateriaalit ovat suljetuilla sivustoilla. Otavan lyhyen matematiikan Huippu-sarjan avoin, sähköinen lisämateriaali https://www.geogebra.org/m/HTChjd2p#material/F9DALcWL ja Otavan pitkän matematiikan Juuri-sarjan materiaali https://www.geogebra.org/m/IhEGYWZS

[4]   Nevala, E. Toiminnallisuutta peruskoulun matematiikkaan Bagdad-näyttelystä. Diplomityö, Tampereen teknillinen yliopisto, 2015.

[5]   Sympsionics. Platonin kappaleiden rakentaminen. Uusi painos Deltaspektri, 2017. Kirjan esittely oli Dimensiossa 6/2014 s. 59.

[6]   Esimerkiksi wikipedia-artikkelit https://fi.wikipedia.org/wiki/Antiprisma (suom.) ja  https://en.wikipedia.org/wiki/Antiprism (engl.)

[7]   Suvanto, M.  3D-mallinnus ja tulostaminen matematiikan opetuksessa. Pro gradu -työ, Helsingin yliopisto, Matematiikan ja tilastotieteen laitos, 2015. Saatavana https://core.ac.uk/download/pdf/33733204.pdf.

[8]   Geogera-materiaali (engl.) Nets of solids osoitteessa https://www.geogebra.org/m/pCv2EvwD

[9]   Geogebra.materiaali (engl.) Which net matches the displayed solid? osoitteessa https://www.geogebra.org/m/n6EjQDw8#material/GmAtu4gt

[10]   Haslinger, C. Constructive Solid Geometry in Education osoitteessa https://www.uni-salzburg.at/fileadmin/multimedia/Mathematik/images/EMMA/Workshop_Turkey/education_days/CSG_Haslinger_low_quality.pdf

[11]   Wolfram Alpha. Examples for Solid Geometry osoitteessa https://www.wolframalpha.com/examples/mathematics/geometry/solid-geometry/

[12]   Mil, J. Kepler-Poinsot polyhedrons osoitteessa https://www.geogebra.org/m/p5gPPkpG

[13]   Kettner, L. 3D Polyhedral Surfaces osoitteessa https://www.ics.uci.edu/~dock/manuals/cgal_manual/Polyhedron/Chapter_main.html