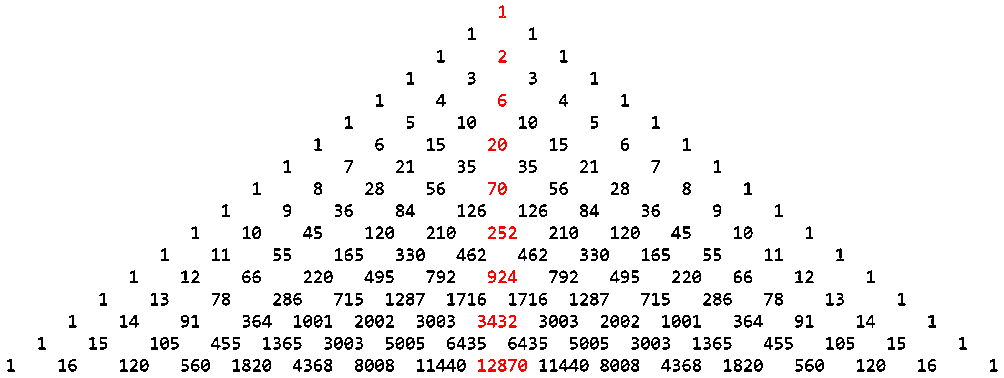
1, 2, 6, 20, 70, 252, …?
Koulumatematiikassa lukujonot ovat sekä apuvälineitä alaluokilla että opetuksen kohteita lukiossa. Monet niistä toimivat myös mainioina pulmatehtävinä, kun jonosta annetaan vain muutamia lukuja alusta ja kysytään, miten jono jatkuu. Pelkästään lukuja tarkastelemalla on aika vaikea keksiä, mikä on jonon 1, 2, 6, 20, 70, 252, … seuraava luku. Jos haluat vaivata päätäsi, niin älä avaa heti tämän jutun koko tekstiä, vaan yritä keksiä ratkaisu itse.
Lukujonoja käyttävät sekä pienet lapset että ammattimatemaatikot. Niillä on suuri merkitys lukukäsitteen oppimisessa, kun lukuja luetellaan yhden, kahden, kolmen jne. välein tai kerrannaisin sekä ylös- että alaspäin. Niitä käytetään sarjakehitelmissä, kun halutaan korvata monimutkaisissa lausekkeissa esiintyvät hankalat funktiot yksinkertaisemmilla lausekkeilla laskujen helpottamiseksi. Ovatpa jonojen ominaisuudet, esimerkiksi suppeneminen, itsenäinenkin matematiikan tutkimuskohde.
Jos internet on käytettävissä, niin lukujonojen kanssa ei tarvitse nykyään paljon päätään vaivata. Kokonaislukujonojen verkkosanakirjassa OEIS on selostettu yli 300 000 jonoa. Toiminnaltaan automatisoidussa lukujonojen verkkotietokannassa (machine generated Sequence Database) on lähes 2,5 miljoonaa lukujonoa (joulukuussa 2020).
Matematiikkataidoillesi voi olla eduksi pohtia itse, minkä säännön mukaan outo lukujono on muodostettu. Tällöin apua on muutamien perusasioiden tuntemisesta. Onko peräkkäisten jäsenten erotus vakio (aritmeettinen jono)? Vai onko peräkkäisten jäsenten suhde vakio (geometrinen jono)? Sääntö voi myös olla jäsenen järjestysluvun funktio (analyyttinen jono) tai seuraava jäsen voidaan laskea edellisten jäsenten perusteella (rekursiivinen jono). Monille rekursiivisille jonoille voidaan löytää myös analyyttinen lauseke.
Entä sitten otsikkojonomme 1, 2, 6, 20, 70, 252, …? Se ei näytä aritmeettiselta eikä geometriselta. Analyyttinen lauseke on olemassa, mutta sitä on varmaankin aika vaikea keksiä:
$f\left(n\right)=\binom{2n}{n}=\frac{\left(2n\right)!}{\left(n!\right)^2}$ , kun n = 0, 1, 2, …
Se ei ole mikä tahansa satunnainen, vain vaikean tehtävän laatimiseksi keksitty funktio. Jonon jäsenet ovat nimittäin keskimmäiset binomikertoimet (engl. central binomial coefficient). Binomikertoimia on parillinen määrä, kun binomi korotetaan parittomaan potenssiin, ja pariton määrä, kun eksponentti on parillinen. Siten vain jälkimmäisessä tapauksessa kertoiminen joukossa on keskimmäinen jäsen. Jonomme jäsenet on siis poimittu Pascalin kolmion parillisilta riveiltä!