David Tallin kolme matematiikan maailmaa

David Tall on tunnettu kolmesta matematiikan maailmastaan. Hän on jäänyt eläkkeelle professorinvirastaan vuonna 2006, mutta on jatkanut tutkimustyötään ja julkaissut senkin jälkeen yhdeksättäkymmentä artikkelia tai kirjaa omalla nimellään tai yhdessä muiden kanssa [1].

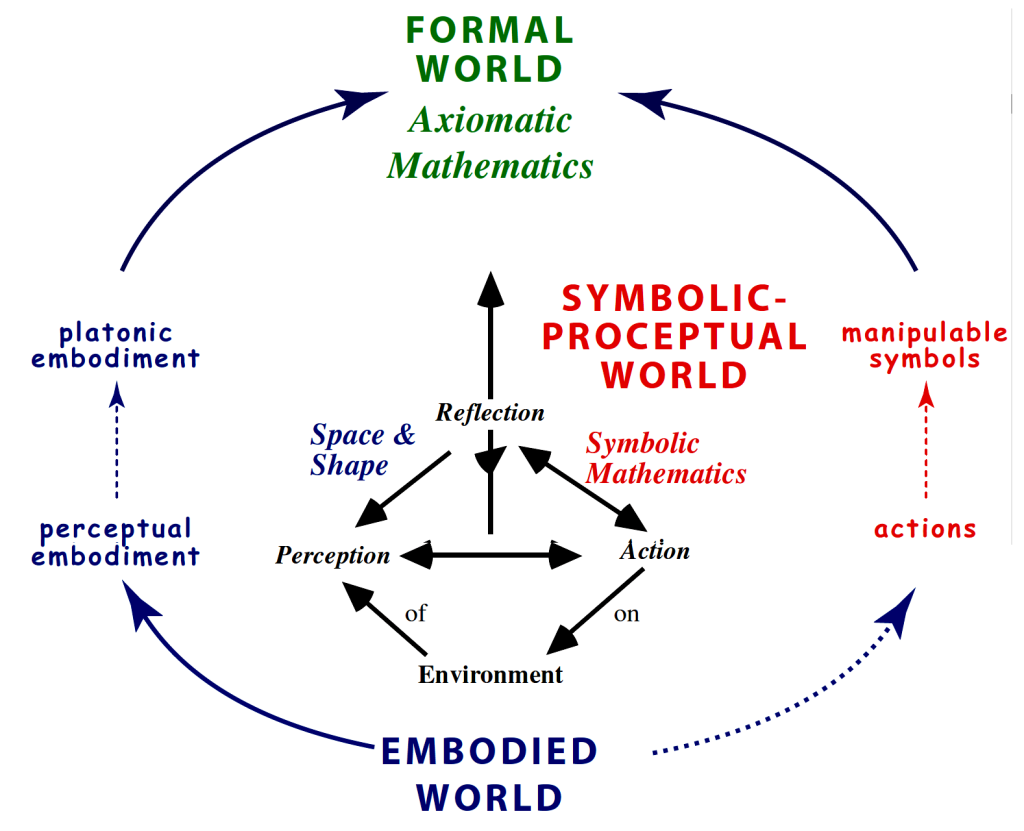
Tall esittää, että on kolmenlaista matematiikkaa. Ne ”ovat niin erilaisia, että ne näyttävät elävän kolmessa erillisessä maailmassa” [2], [3]. Ensimmäinen on aistihavaintojen maailma. Ei sellaisena konkreettisena ja objektiivisena kuin sitä usein ajatellaan filosofisen olemassaolon mielessä, vaan aistihavaintojemme pohjalta muotoutuneiden mielikuvien ja käsitteiden toteutumana tai ruumiillistumana (engl. concept embodiment). Toisin sanoen maailma sellaisena kuin itse kukin havaitsija sen mieltää ja ymmärtää. Siis jotain Platonin luolavertauksen kaltaista.

Oppiminen, myös matematiikan oppiminen, rakentuu näiden mielikuvien varaan. Niin ollen on helppo ymmärtää, miten tärkeitä ovat jo ensimmäisten vuosien aikana saadut kokemukset ja miten suuria oppimiserot voivat niiden pohjalta olla. Useimpien ihmisten matematiikkakuva muodostuu sitten koulumatematiikan perusteella, sillä muita vaikutteita matematiikasta tulee useimmille lapsille vain harvoin. Se kuva ei ole tai ei ainakaan ole aina ollut jäsentynyt ja kiehtova, vaan päinvastoin monesti sekava ja jopa vastenmielinen, suorastaan pelottava. Parempaan pyritään kuitenkin koko ajan [4].

Toinen matematiikan laji on symbolien maailma. Siellä elävät luvut ja niillä laskeminen, kuviot, funktiot jms. Tall on luonut tämän maailman luonnehtimiseksi sanan ”proceptual” joka viittaa yhtäältä prosesseihin (engl. processes), esimerkiksi laskutoimitusten suorittaminen, ja toisaalta käsitteisiin (engl. concepts), esimerkiksi yhteenlasku [2, s. 2]. Tällä sanalla hän haluaa korostaa sitä, että ”symbolinen” on sanana liian monikäsitteinen ja että tämän maailman jakaminen esimerkiksi numeerisiin, algebrallisiin ja geometrisiin tms. osiin hämärtää tajun siitä, että oppimisessa on kyse kokonaisprosessista [2, s. 23].  

Kolmas maailma on muodollisen matematiikan maailma. Sinne kuuluvat aksioomat, määritelmät, lauseet ja todistukset, siis sellainen matematiikka, josta koulumatematiikan kritisoijat käyttävät joskus nimitystä ”oikea matematiikka”. – Ajan mittaan Tall on korostanut yhä vähemmän näiden maailmojen erillisyyttä ja pikemminkin pyrkinyt rakentamaan yhteyksiä niiden välille (kuva). Tallin maailmat voidaankin nähdä myös matematiikan oppimisen portaina aina varhaisesta lapsuudesta kouluopetuksen kautta yliopistomatematiikkaan [5].

Tämä eteneminen vertautuu Varga–Neményi-menetelmän [6], [7] abstraktion tiehen [8]: ”Abstraktion tie on metafora, jolla kuvataan oppimisen ja opettamisen eri vaiheita konkreettisesta toiminnasta kohti abstraktia ajattelua ja ilmaisua. Uuteen asiaan tutustuminen lähtee liikkeelle oppilaiden omista välittömistä kokemuksista, jotka voivat olla arjen tilanteita, pelejä tai ohjattuja leikkejä”. Toisessa vaiheessa oppilas muodostaa toimintavälineitä käyttäen mielikuvia, joiden pohjalle matemaattiset käsitteet rakentuvat abstraktion tien kolmannessa vaiheessa. Keskeinen ajatus tässä on se, että liikenne on kaksisuuntaista, sillä aina tarvittaessa voidaan palata takaisin hakemaan tukea edellisistä vaiheista.

Tallin kolme maailmaa eivät ole suinkaan ainoa matematiikkaa luonnehtiva kolmijakomalli. Esimerkiksi Ernestin mukaan [9] matematiikka on yhtäältä johdonmukainen, staattinen ja yhtenäinen tietojärjestelmä, jota logiikan lait pitävät koossa (platonistinen käsitys). Tämä vastaa selvästi Tallin muodollisen matematiikan maailmaa. Toisaalta matematiikka voidaan nähdä ihmisen keksimänä, uusien ongelmien kautta kehittyvänä, dynaamisena järjestelmänä, jota kukin matemaatikko (ja oppija) kehittää omien ajatustensa mukaan. Tämä taas vastaa ainakin lähtökohdiltaan Tallin ensimmäistä maailmaa. Ernestin kolmannen luonnehdinnan mukaan matematiikka on tosiasioista, menetelmistä ja säännöistä koostuva työvälinekokoelma. Tässä käsityksessä on paljon Tallin toisen maailman piirteitä.

Suomalaiset opettajankouluttajat ovat kehittäneet Tallin kolmen maailman pohjalta kuusiosaisen mallin. Matematiikan tekemisen ja oppimisen voidaan nähdä olevan jatkuvaa vuoropuhelua tekijän/oppijan subjektiivisten mielikuvien ja matematiikan objektiivisen rakenteen välillä. Tämä kahtiajako yhdistettynä Tallin kolmeen maailmaan muodostaa oppimisen kulkua kuvaavan kuusikentän [10], [11].  

Tallin kokonaistuotanto on valtava. Se sisältää enemmän kuin kolme ja puoli sataa nimikettä [1]. Hänen ajatuksensa ovat osin vaikeaselkoisia. Matematiikkamaailmojen malli on myös kehittynyt tai ainakin muuttunut vuosien kuluessa. Näistä syistä kokonaiskuvan muodostaminen osoittautui niin työlääksi, että en ole yrittänytkään pyrkiä sellaista muodostamaan tässä jutussa. Lisää tietoa Tallista ja hänen elämänvaiheistaan saat halutessasi hänen elämäkerrastaan [12].

Lähteitä ja lisää luettavaa

[1] David Tall in Google Scholar, viitattu 3.9.2023, osoitteessa https://scholar.google.co.uk/citations?hl=en&user=IV1rmyEAAAAJ&view_op=list_works&sortby=pubdate

[2] Tall, David (2002): Three Worlds of Mathematics. Presentation in Taipei, October 14th, 2002, osoitteessa https://www.researchgate.net/publication/246523544_Introducing_Three_Worlds_of_Mathematics/link/53eb48f60cf2fb1b9b6b09c3/download

[3] David Tall’s Research Themes, The University of Warwick, Mathematics Education Research Center, viitattu 3.9.2023, osoitteessa https://homepages.warwick.ac.uk/staff/David.Tall/themes/three-worlds.html

[4] Kivistö, Pinja-Sofia (2019): Matematiikkakuvan osa-alueet ja myönteisen matematiikkakuvan tukeminen matematiikan opetuksessa. Kandidaatintutkielma, Oulun yliopisto. Viitattu 4.9.2023 http://jultika.oulu.fi/files/nbnfioulu-201905031594.pdf

[5] Tall, David (2010): The Transition to Formal Thinking in Mathematics osoitteessa https://homepages.warwick.ac.uk/staff/David.Tall/pdfs/dot2008e-merj-3worlds.pdf

[6] Lampinen, Anni (2020): Entäpä jos huonoa laskupäätä ei olekaan. Artikkeli on ilmestynyt alun perin Suomi–Unkari-lehdessä 3/2008. Saatavissa osoitteesta https://suomiunkari.fi/kouluille/entapa-jos-huonoa-matikkapaata-ei-olekaan/

[7] Lampinen, Anni ja Korhonen, Hannu (2010): Matematiikka kuuluu kaikille. Dimensio 1/2010 s. 18–22, https://drive.google.com/file/d/1XUHi_OCIDOdL2sYQBMXD-drkTUy9cyH_/view

[8] Lampinen, Anni (2015): Abstraktion tie. Osoitteessa (viitattu 5.9.2023) https://varganemenyi.fi/menetelma/tietoa-menetelmasta/varga-nemenyi-menetelma/24-menetelman-osiot/37-abstraktion-tie

[9] Kailio, Jarmo (2010): Matematiikan aineenopettajaopiskelijoiden ja luokanopettajaopiskelijoiden matematiikkakuvan sekä pedagogisen ajattelun vertailua, s.10. Pro gradu -tutkielma, Jyväskylän yliopisto. [10] Hannula, Jani (2014): Matematiikan kuusi osaa: David Tallin matematiikan kolmen maailman viitekehyksen laajentaminen Juha Oikkosen matematiikan kaksilla kasvoilla. LUMAT 2(1), 2014, osoitteessa https://journals.helsinki.fi/lumat/article/view/1082/1075

[11] Oikkonen, Juha ja Hannula, Jani (2022): The three worlds and two sides of mathematics and a visual construction for a continuous nowhere differentiable function. LUMAT Special Issue 2022, osoitteessa https://journals.helsinki.fi/lumat/article/view/1693/1679

[12] David Tall’s curriculum vitae osoitteessa https://homepages.warwick.ac.uk/staff/David.Tall/pdfs/prof-david-tall-cv.pdf

Kiitokset tästä jutusta kuuluvat Päivi Perkkilälle, joka ehdotti jutun kirjoittamista ja on ohjannut sen rakentumista Talliin liittyvillä muistikuvillaan ja monilla lähdevihjeillä.