En ny matematikklubb för hela Svenskfinland!
Samhällets behov av matematiskt kunniga har länge varit stort, och det bara växer. Möjligheterna att få intressant och trivsamt jobb för den som har läst matematik är utmärkta. Trots det, och trots att lärarna i skolorna gör ett utmärkt arbete, verkar inte antalet unga som väljer att studera matematik bli större. För att erbjuda en bild av matematik, som kompletterar den bild som skolan ger, och för att lyfta fram matematik som hobby, har många universitet i Finland nu satsat på att starta matematikklubbar, i samarbete med MAOL och Finlands matematiska förening. Här presenterar vi Åbo Akademis svenskspråkiga matteklubb, som är riktad till alla matematikintresserade i grundskolans högre årskurser eller gymnasiet.
Klubbens vision
Nyttoaspekten av matematik är viktig: Varför och hur behövs matematik? Vilken nytta kan man själv ha av matematik, t.ex. ifall man väljer att göra matematik till sitt yrke?
Klubbens avsikt är ändå mera att lyfta fram det vackra i matematik: nöjet att i lugn och ro få fundera på ett roligt problem, utforska egna lösningsidéer utan att alls bedömas, och sedan få njuta av känslan av att till sist ha klarat att lösa ett utmanande problem, ensam eller i samarbete med andra matematikintresserade. Målet är att inspirera deltagarna till att göra mera matematik, och den ofta överskattade begåvningens betydelse tonas ner.
Klubben vill erbjuda alla matematikintresserade i Svenskfinland sällskap av likasinnade, oberoende av var man bor. För att klubben ska passa så många som möjligt, ska uppgifterna och deras lösning inte kräva mycket förkunskaper, utan logiska resonemang är viktigast. Diskussionen i klubben ska ändå vara fri, så man kan på deltagarnas begäran naturligtvis fördjupa och bredda något, som redan har undervisats i skolan. Det finns allt från lätta till mycket utmanande uppgifter, för att alla ska hitta ett lagom utmanande problem att klura på.
Hur fungerar klubben i praktiken?
Klubbens upplägg är flexibelt och det utvecklas vartefter vi får förbättringsidéer, men just nu är alla träffar per videomöte. Det här är ett naturligt val då vi vill nå hela Svenskfinland, och avsikten är att klubben senare hålls enligt ett hybridformat. Träffarna hålls fysiskt i matematikens utrymmen vid Åbo Akademi, men på ett sådant sätt att man också kan delta per videokonferens.
Wickholm. Mikael Kurula vid Åbo Akademi står i bakgrunden för klubbens kontinuitet.
Bild: Mikael Kurula
En träff börjar ofta med att man tillsammans bekantar sig med dagens tema en liten stund, och sedan börjar man jobba självständigt med uppgifter på samma tema. Uppgifterna börjar ganska lätt och sedan blir de klurigare vartefter. Klubbledaren finns på plats för att hjälpa och tipsa, så att man säkert kommer vidare med den uppgift som man har valt, och man går framåt i sin egen takt. Man kan stanna kvar och lösa i det gemensamma rummet om man vill, eller så kan man gå till ett eget rum i en mindre grupp för att samarbeta. Uppgifterna finns alltid på klubbens webbsida, som är tillänglig bara för medlemmarna, så man kan arbeta med dem också mellan liveträffarna. Ledaren svarar också på frågor som kommer in mellan träffarna.
Man måste inte delta varje gång, och det finns inga andra måsten heller, utan allt är frivilligt. För att kunna delta behöver man bara en dator, pekplatta eller smarttelefon, penna, papper och huvud. Klubben är gratis för deltagarna. Du som vill bekanta dig närmare med klubben, gå till https://matematiikkakilpailut.fi/kerhot/abo/
Hur kan en uppgift se ut?
Vid varje träff finns många uppgifter av växande svårighetsgrad. Klubben fokuserar inte på tävlingar, men det material, som Finlands matematiska förenings träningssektion ger till klubben, behandlar grunderna i tävlingsmatematik. De klubbdeltagare, som småningom har gått igenom dessa grunder, som en del av klubbens mångsidiga verksamhet, kan börja ta sig an uppgifter från nationella och internationella tävlingar. Också tävlingar finns på många olika nivå, där internationella matematikolympiaden är den mest krävande. I matematik får alla möjligheten att möta sina egna gränser, och det är alltså viktigt att minnas att man inte ska låta sig slås ner av att man troligen inte kan lösa alla uppgifter utan hjälp.
Ett exempel på en lätt fråga (efter att man har diskuterat multiplikationsprincipen, som ligger som grund för kombinatoriken) kan vara:
”I en låda finns 5 hattar och 6 halsdukar. Hur många
olika hatt/halsduk-kombinationer kan man få?”
Till näst ger vi två exempel på mellansvåra uppgifer, som också visar hur uppgifterna ibland bygger på varandra för att utveckla tänkandet längre.
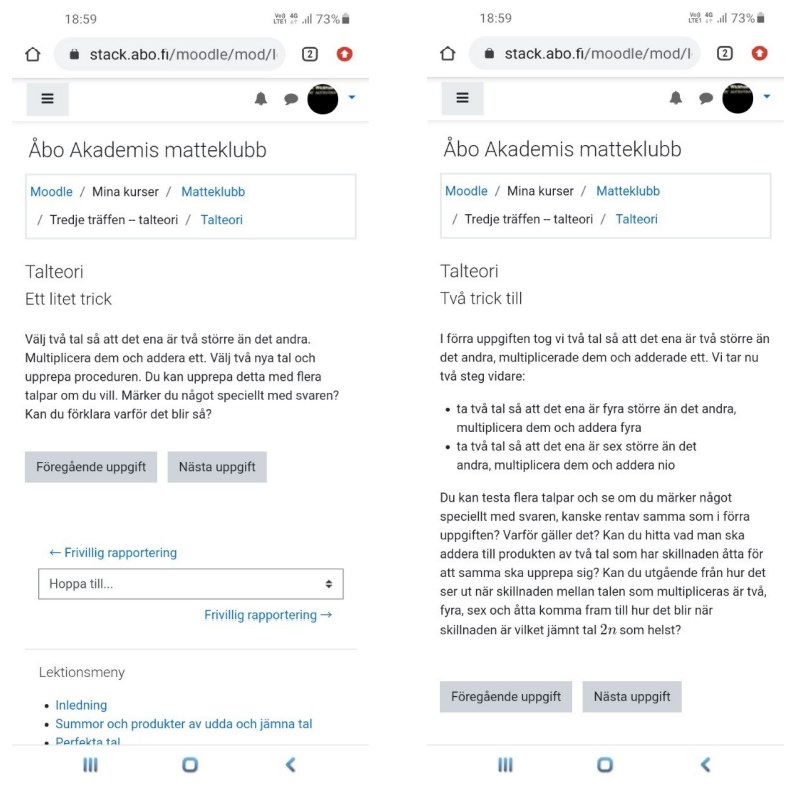
Uppmaningarna i de här uppgifterna kan först verka slumpmässiga – det är kanske inte klart varför man ska göra just så. Efter att ha testat några talpar kommer sedan aha-upplevelsen: man får alltid en jämn kvadrat. Utforskandet tar inte slut där, utan man vill förstås också veta varför det blir som det blir, och snart har man själv upptäckt kvadreringsregeln.
Vi ger också exempel på en utmanande uppgift, som handlar om färgläggningar av punkter i planet $\mathbb R^2$. Uppgiften är följande:
”Varje punkt i planet är färgad antingen röd, grön eller blå, så att t.ex. $(1,0)$ kan vara röd och $(-\pi,\sqrt 3)$ blå. Bevisa att det finns punkter med samma färg vars avstånd är 1.”
Man kan lösa uppgiften med ett motsägelsebevis, vars konstruktion illustreras i GeoGebra här bredvid. Du kan släpa runt punkten $B$ i GeoGebra-appen för att rita upp en röd cirkel med punkten $A’$. Beviset går ut på att konstruera den här cirkeln och sedan dra följande slutsats: eftersom den röda cirkeln har diameter större än $1$, så finns det två punkter på cirkelperiferin, som ligger på avståndet $1$ från varandra.
Dynamisk illustration av beviset med GeoGebra. Släpa runt punkten $B$ för att rita upp en röd cirkel med punkten $A’$. GeoGebra applet: Mikael Kurula
Anta alltså det motsatta, att motsatsen till påståendet gäller: varje par av punkter i planet på avståndet $1$ från varandra är av olika färg. Vi ska använda den här antitesen för att konstruera en motsägelse. Lösningen bygger på en tidigare uppgift, ur vilken det följer att om man bara använder två färger, så finns det punkter av samma färg på avståndet $1$. Om antitesen gäller, så måste det alltså finnas en röd punkt i planet.
Rita nu en cirkel med radie $1$ och en röd punkt $A$ som mittpunkt. Punkterna på cirkelns periferi måste då vara antingen gröna eller blåa, eftersom de ligger på avståndet $1$ från den röda mittpunkten. Eftersom det finns punkter på cirkelperiferin, som ligger på avståndet $1$ från varandra, så måste det finnas både blåa och gröna punkter på cirkelperiferin. Välj en blå punkt $B$ och en grön punkt $C$ på cirkelperiferin, som ligger på avståndet $1$ från varandra. Speglingen $A’$ av punkten $A$ i kordan $f$ mellan $B$ och $C$ måste vara röd, eftersom den ligger på avståndet $1$ från både $B$ och $C$.
Vi konstruerade i förra stycket en röd punkt $A’$ på cirkeln med radie $\sqrt{3}$ och mittpunkt $A$. Omvänt kan varje punkt på den cirkeln konstrueras på samma sätt, aftersom kordan $BC$ som speglingen sker i lätt kan konstrueras för varje punkt $A’$. Därför måste alla punkter på cirkeln med radie $\sqrt{3}$ vara röda. Eftersom den cirkeln har diameter större än 1, så finns det två punkter på avståndet ett på den här cirkeln. Vi har nu konstruerat två röda punkter, som ligger på avståndet 1, vilket motsäger antitesen. Antitesen är alltså falsk, eftersom den leder till en motsägelse, och vi har bevisat påståendet.
Klubbdeltagaren kan gärna själv konstruera GeoGebra-appen för att lösa uppgiften, med tips från ledaren. Lägg också märke till att det är mycket lättare att förstå den ovan givna lösningen än att själv producera den.
Hur har klubben lyckats hittills?
En kärngrupp på ungefär tio personer som brukar delta i alla träffar har formats. Den geografiska spridningen är stor, med deltagare från Österbotten, Nyland och Åboland. Det finns förstås plats för flera, då verksamheten fortsätter på hösten. Ifall gruppen växer märkbart, så har vi möjlighet att dela den och ordna flera träffar.
Uppgifterna har överlag fått positiv respons, och olika deltagare har berömt olika uppgiftsserier, vilket visar att variation är viktig. Videokonferensformatet har fungerat rätt bra, men som väntat har det också gett vissa utmaningar för ledaren. Det är inte alltid lätt att veta om någon har kört fast, så klubbmedlemmen behöver själv ta initiativ, och det är inte alltid lätt att veta hur man ska försöka hjälpa till när det är svårt att se hur deltagaren har börjat på med en lösning.
En deltagare tycker att det var på tiden att klubben startades:
“Jag har länge önskat att det skulle finnas en sådan här matteklubb, med andra som är extra intresserade av matematik och med mer utmanande uppgifter än de vi får i skolan.”
En annan deltagare tycker att träffarnas längd (en timme) och tidpunkt (sen eftermiddag) är lagom, för att det finns tid att göra något både mellan skolan och klubben och efter klubben. Båda upplever att de har lärt sig en hel del nytt, och också att det finns ganska mycket man kan göra utan att behöva ha så värst mycket specialkunskaper.
Är du intresserad av att starta en klubb i ditt eget gymnasium?
Det finska matematikgymnasiet i Månsas i Helsingfors erbjuder både ekonomiskt och innehållsmässigt stöd till lärare som vill starta en lokal matematikklubb i sitt gymnasium. Läs mera här: https://www.mayk.fi/perusta-matematiikkakerho/







