Evoluutta
Evoluutta on käyrän kaarevuuskeskipisteiden ura. Ei sitä eikä kaarevuuden käsitettä muutenkaan ole käsitelty paljon koulukursseissa, ehkä käsin piirtämisen vaikeuden takia. Sähköiset matematiikkatyövälineet, esimerkiksi GeoGebra, avaavat kuitenkin aivan uusia mahdollisuuksia. Perustietoja on helposti saatavissa verkosta.
On kaksi käyrää, joiden kaarevuus on vakio: suora ja ympyrä. Edellinen ei ole lainkaan kaareva. Jälkimmäinen taas on sitä kaarevampi, mitä pienempi sen säde on (kuva 1). Ympyrän kaarevuuden mitaksi sopii siten säteen käänteisluku $k=\frac{1}{r}$. Kaarevuus kasvaa rajatta, kun ympyrä pienenee. Vastaavasti kaarevuus pienenee kohti nollaa, kun ympyrä suurenee, ja näkyvissä oleva osa ympyrästä lähestyy suoraa. Kansainvälisessä yksikköjärjestelmässä kaarevuus voitaisiin määritellä toisinkin: käyrän tangenttivektorin tai suuntakulman derivaattana kaarenpituuden suhteen [1].

Muiden käyrien kaarevuus vaihtuu käyrän pisteestä toiseen. Kaarevuutta voidaan havainnollistaa piirtämällä käyrää sivuava ympyrä – kaarevuusympyrä – käyrän kuhunkin pisteeseen. Esimerkiksi paraabelin kaarevuus [2] on suurin huippupisteessä (kuva 2).
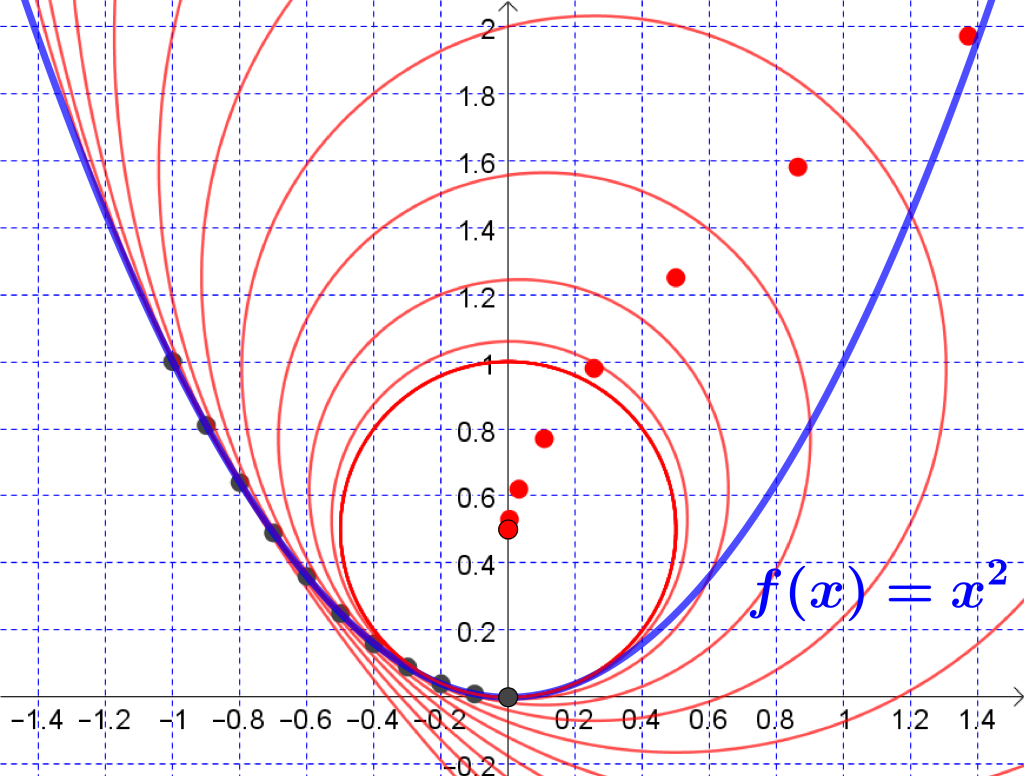
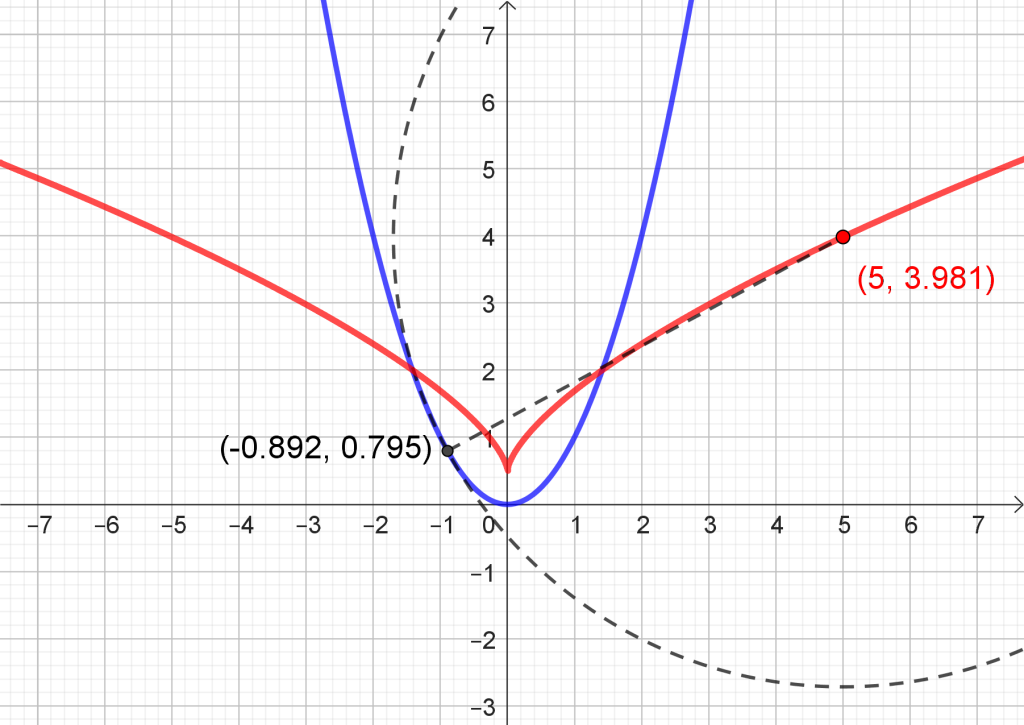
Kaarevuusympyröiden keskipisteiden ura on nimeltään evoluutta. Perusparaabelille sen yhtälö on y:n suhteen ratkaistussa muodossa [3] (kuva 3)
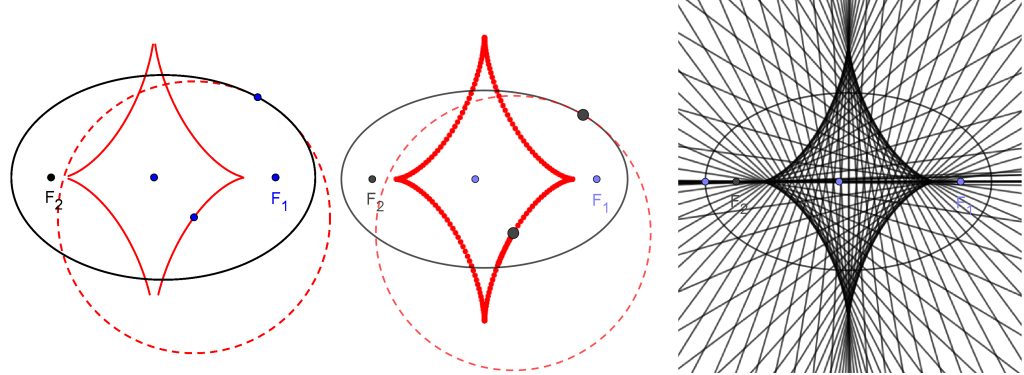
Sanalla ’evoluutta’ ei ole eikä sille tiettävästi ole edes koskaan yritetty tarjota omakielistä vastinetta [4]. Kaarevuuskeskipisteiden uria tutki Christian Huygens jo 1600-luvulla, mutta sana on peräisin 1700-luvun alusta [5]. Evoluutta voidaan piirtää monella tavalla, esimerkkinä ellipsi (kuva 4).
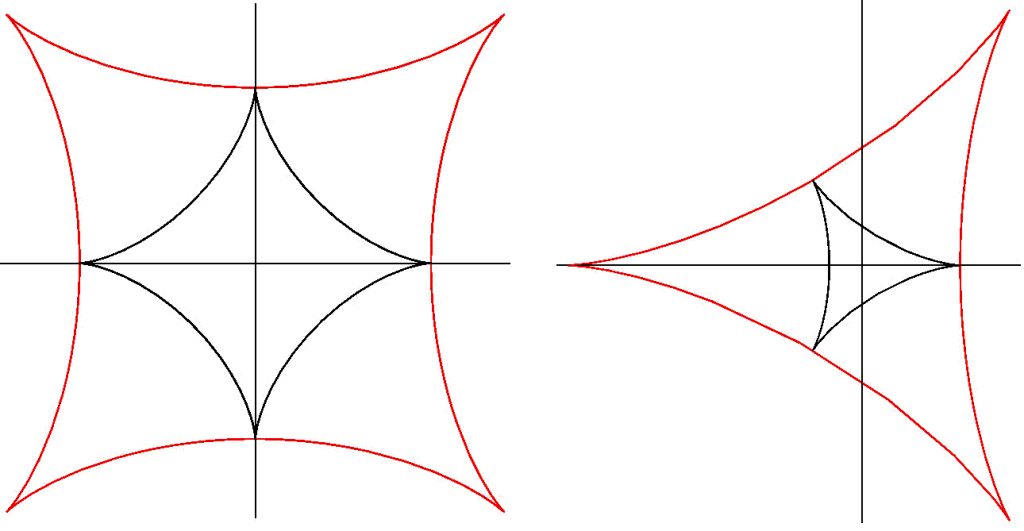
Kuvista 3 ja 4 nähdään, että käyrä ja sen evoluutta ovat usein muodoltaan hyvin erilaisia. On kuitenkin mielekästä kysyä, onko sellaisia käyriä, jotka ovat yhteneviä tai edes yhdenmuotoisia evoluuttansa kanssa. Yhteneviä ei ole, mutta yhdenmuotoisia on, esimerkiksi deltoidi ja astroidi [7] (kuva 5).
Lähteitä ja lisää luettavaa
[1] Kurki-Suonio, Kaarle: Kaarevuus matematiikassa, fysiikassa ja EU:ssa. Dimensio 3/2012 s. 23–24. Saatavissa myös osoitteesta https://www.mv.helsinki.fi/home/kurkisuo/6.2.D/12-Dim-Kaarevuus.pdf
[2] Jacobsen, Erik: Circle of Curvature for a Parabolic Path osoitteessa https://www.geogebra.org/classic/wuhq8fkt
[3] Wolfram Mathworld: Parabola Evolute osoitteessa https://mathworld.wolfram.com/ParabolaEvolute.html
[4] Lehtinen, Matti: Matematiikan sanoja. Eukleides-kirjat, 2017.
[5] Merriam–Webster: Evolute osoitteessa https://www.merriam-webster.com/dictionary/evolute#h1
[6] Wolfram Mathworld: Elllipse Evolute osoitteessa https://mathworld.wolfram.com/EllipseEvolute.html
[7] Wolfram Mathworld: Evolute https://mathworld.wolfram.com/Evolute.html







