Interventiotutkimus kolmasluokkalaisten murtolukujen oppimisesta ”Ylhäällä olevat vaan plussataan”
Väitöstutkimuksessa testattiin lyhyen intervention vaikutusta oppilaiden suoritukseen. Aikaisempien tutkimusten perusteella murtoluvun suuruuden ymmärtäminen ja konkreettiset välineet näyttäisivät olevan ”avain” murtolukulaskujen hallitsemiseen. Tutkimuksessa saatiin pieniä eroja aikaiseksi erityisesti matematiikkaa heikommin osaavien oppilaiden kohdalla. Tutkimuksesta on hyötyä kaikille peruskoulun opettajille, joita tulos toivottavasti rohkaisee murtokakkupalojen hyödyntämiseen opetuksessaan.
Rationaaliluvuilla on kaksi symbolista merkitsemistapaa: murtolukumerkintä ja desimaalilukumerkintä. Alakoulun matematiikassa näitä kahta merkitsemistapaa tarkastellaan usein erikseen ja siksi opetuksessa ei puhuta ”rationaalilukujen laskutoimituksista” vaan esimerkiksi ”samannimisten murtolukujen vähennyslasku” tai ”desimaalilukujen yhteenlasku”. Väitöstyössä keskitytään tarkastelemaan erityisesti rationaalilukujen murtolukuesitystä.
Anu Tuominen (KT, FL) väitteli keväällä 2021 murtolukujen oppimisesta alakoulun kolmannella luokalla. Mikä sai matematiikan opettajan ja opettajankouluttajan tutkimaan murtolukujen oppimista? Opettaessani lukiolaisia huomasin, että osa opiskelijoista ei hallinnut murtoluvuilla laskemista. Esimerkiksi todennäköisyyslaskennassa opiskelija ei tiennyt, miten toimia laskiessaan murtolukuina esitettyjä todennäköisyyksiä yhteen tai kertoessaan niitä. Asia oli siis jäänyt yläkoulussa oppimatta. Opettaessani yläkoulussa oppilaita huomasin, että samannimisten murtolukujen yhteen- ja vähennyslasku sujuivat mutta esimerkiksi murtolukujen kertominen ja jakaminen luonnollisella luvulla oli epävarmaa. Oppilaalla ei ollut mitään käsitystä siitä, kuinka suuri vastauksen tulisi olla. Oppilas teki vain jotain osoittajalle tai nimittäjälle tai molemmille. Tämä asia oli siis jäänyt alakoulussa oppimatta.
Taustaa
Lapset tutustuvat luonnollisiin lukuihin hyvissä ajoin jo ennen kouluikää. Alaluokilla käsitys luvuista ominaisuuksineen saa entisestään vahvistusta: Seuraava luku saadaan luettelemalla, jokaisella luvulla on yksikäsitteinen merkintätapansa, kertominen kasvattaa ja jakaminen pienentää ja luonnolliset luvut sijaitsevat lukusuoralla tasaisin välein. Mikään edellä oleva ei kuitenkaan pidä enää paikkaansa rationaalilukujen kohdalla. Oppilaat tekevät ”kummallisia” virheitä, esimerkiksi erinimisten murtolukujen yhteenlaskussa 1/2 + 1/3 = 2/5 ns. tuplalaskun. Kun 7.-luokkalaisilta oppilailta kysyttiin, kuinka monta murtolukua on 1/4 ja 1/3 välissä, niin useassa paperissa lueteltiin luvut 2/4, 3/4, 4/4, 0/3. Vastauksesta näkee, että oppilas ei ole ajatellut minkä kokoisia hänen luettelemansa luvut ovat. Myös desimaalilukujen suuruusvertailussa oppilas saattaa nojautua luonnollisten lukujen ominaisuuksiin (Natural Number Bias) ja päätellä niiden perusteella, että 0,19 > 0,3, koska 19 > 3. Oppilas ikään kuin sivuuttaa luvun alussa olevan nollan ja vertailee keskenään ”lukuja” pilkun oikealla puolella.
Murtolukujen opettaminen saattaa näyttäytyä oppilaille tutusta matematiikasta ”irrallisena”. Murtolukujen merkintätapa on erilainen kuin kokonaisluvuilla, suuruusvertailu noudattaa erilaisia periaatteita kuin esimerkiksi desimaalilukujen suuruusvertailu ja laskuproseduurit ovat totutusta poikkeavia. Ominaisuus, joka sitoo murtoluvut tuttujen kokonaislukujen kanssa samaan lukusuoraesitykseen, on luvun suuruus. Symboliset esitysmuodot esimerkiksi 2 ja 4/2 osoittavat lukusuoralla samaan kohtaan, vastaavasti desimaalilukuesitys 0,5 ja murtolukuesitys ½ osoittavat samaan kohtaan lukusuoralla. Tätä luvun suuruusominaisuutta tulisikin korostaa ja sen avulla linkittää murtoluvut aiemmin opitun matematiikan joukkoon. Osalle oppilaista matematiikka näyttäytyy sääntökokoelmana, irrallisina faktoina, kun sen pitäisi olla verkosto, asiat linkittyvät toisiinsa ja oppilaan tulisi huomata yhteyksiä aiemmin opittujen asioiden välillä. Esimerkiksi pystyäkseen sijoittamaan murtoluvun 7/2 lukusuoralle tulee oppilaan joko ymmärtää että murtoluvussa on seitsemän puolikasta tai suorittaa jakolasku 7:2. Tämän artikkelin otsikossa oleva lainaus ylhäällä olevat vaan plussataan on suoraan kolmasluokkalaiselta oppilaalta. Oppilaan opettaja oli antanut hänelle tällaisen ohjeen. Ohje on proseduurin kannalta aivan oikea mutta tällaiset hyväntahtoiset oikotiet ilman tarkempaa perustelua ovat omiaan luomaan matematiikasta irrallista temppukokoelmaa. Mistä oppilas tietää milloin ”ylhäällä oleville” tehdään jotain ja milloin ”alhaalla oleville”?
Kun yläkoulun, lukion tai ammattikoulun opettajilta kysytään, mitkä matematiikan asiat ovat jääneet usealta oppilailta oppimatta, yleensä mainitaan murtoluvut. Murtoluvut koetaan usein vaikeana aiheena oppia ja opettaa. Vuosikymmenistä toiseen on tutkittu murtolukujen oppimista, on tunnistettu tyypillisiä virhekäsityksiä ja testattu erilaisia opetussuunnitelmia ja toteutettu interventioita. Tutkimuksissa hyväksi havaitut menetelmät eivät kuitenkaan siirry käytäntöön koulujen arkeen vaan samat virhekäsitykset löytyvät yhä oppilaiden suorituksissa. Yhtenä ongelmana saattaa olla se, että tutkimuksista raportoidaan kansainvälisesti arvostetuissa julkaisuissa, jotka ovat usein maksumuurin takana. Tieto ei siis saavuta kenttää. Toinen ongelma saattaa olla se, että tutkimusten interventiot ovat olleet viikkojen, jopa kuukausien mittaisia, jolloin ne ovat vaatineet opettajalta paljon aikaa ja paneutumista. Interventio vie myös tilaa muulta opetukselta. Täytyisi siis löytää tehokas opetusmenetelmä, joka on ei vaadi massiivista ajankäyttöä vaan on helppo ujuttaa koulun arkeen ja muun matematiikan opetuksen lomaan.
Tavoitteenani oli suunnitella ja toteuttaa murtolukuihin liittyvä höyhenen kevyt ja neulan terävä interventio. Höyhenen kevyellä tarkoitan sitä, että interventio on ajallisesti lyhyt ja siksi toteutettavissa oppikirjojen murtolukujakson puitteissa. Neulan terävällä tarkoitan sitä, että interventio kohdistuu asian oppimisen kannalta keskeisimpiin sisältöihin ja käsitteisiin huomioiden tyypilliset virhekäsitykset. Oppimisen varhaisessa vaiheessa muodostuneita virhekäsityksiä on myöhemmin vaikea saada muuttumaan. Oppilaiden oppimishistoriaan emme pysty vaikuttamaan, joten hedelmällisin ajankohta toteuttaa interventio on ennen kuin oppilaille on asiaa vielä varsinaisesti opetettu. Näin mahdolliset virhekäsitykset eivät ole päässeet vielä muodostumaan. Kohdejoukoksi valikoituivat kolmasluokkalaiset, sillä useassa matematiikan oppikirjasarjassa samannimisten murtolukujen yhteen- ja vähennyslasku sisältyvät silloin ensimmäisen kerran opiskeltavaan materiaaliin.
Interventio
Opettajayhteistyöverkoston kautta löydettiin yksitoista luokanopettajaa, joiden luokalla murtolukujakso oli sopivasti vasta tulossa. Koska jokainen luokka on hieman erilainen ja jokaisella opettajalla on oma opetustyylinsä, ei ollut mielekästä verrata kahta luokkaa keskenään. Siksi kukin luokka jaettiinkin keskenään mahdollisimman vertailukelpoiseen puolikkaaseen luokanopettajan oppilastuntemusta hyödyntäen. Kummassakin puolikkaassa tuli olla tyttöjä ja poikia, S1- ja S2-oppilaita (S1= suomi äidinkielenä, S2= suomi toisena kielenä), nopeita ja hitaita laskijoita. Alkumittauksessa vielä varmistettiin, etteivät puolikkaat poikenneet toisistaan tilastollisesti merkitsevästi. Interventio kohdistettiin puolikkaaseen, jota opetti tutkimusavustaja. Kontrollipuolikasta opetti luokanopettaja parhaaksi katsomallaan tavalla. Opettajille ei kerrottu etukäteen mitä interventiotunneilla tehtäisiin. Heille luvattiin kuitenkin kattaa samat asiasisällöt, jotta opettajat saattoivat pitää koko luokalleen saman matematiikan kokeen intervention päätyttyä.
Tutkimusavustajat olivat jo pedagogiset opintonsa suorittaneita matemaattisten aineiden aineenopettajaopiskelijoita tai opintojensa loppusuoralla olevia luokanopettajaopiskelijoita. Tutkimusavustajat toteuttivat interventiotunnit ennalta laatimieni tuntisuunnitelmien pohjalta. Tuntisuunnitelmat ja muu interventiossa käytettävä materiaali käytiin yhdessä läpi noin tunnin mittaisena koulutuksena. Interventio oli vain viiden oppitunnin mittainen, ja siinä painotettiin murtoluvun suuruuden ymmärtämistä. Murtoluvun suuruuden hahmottamista tuettiin hyödyntämällä konkreettisia murtokakkupaloja, murtolukupohjaa ja pelaamalla lautapelejä: Pitsa-peliä ja Suurin murtoluku -peliä. Ajatuksena oli tehdä murtoluvut näkyväksi ja siten keventää oppilaiden työmuistin kuormitusta. Näin oppilaiden ei tarvinnut verrata murtolukujen symboliesityksiä keskenään vaan oppilaat saattoivat hyödyntää esimerkiksi suuruusvertailuissa näköhavaintoaan: Se murtoluku, mikä näytti suuremmalta, oli suurempi.
Oppitunneista neljä käytettiin murtolukujen ilmaisemiseen ja suuruusvertailuun ja viidennellä oppitunnilla tutustuttiin samannimisten murtolukujen yhteen- ja vähennyslaskuun. Matematiikan oppikirjoissa laskutoimituksiin käytettiin useampi oppitunti. Interventiotunnilla oppilaat tekivät symbolimuodossa esitettyjä laskutehtäviä ja mallinsivat laskuja murtokakkupaloin. Vastus kirjoitetiin symbolimuodossa. Tavoitteena oli antaa oppilaille tilaa oivaltaa itse yhteen- ja vähennyslaskuun liittyvä laskusääntö. Näin oppilaat ovat mukana oivaltamassa matematiikan laskusääntöjä, eikä niitä anneta heille ylhäältä valmiina. Luokkien interventiopuolikkaat muodostivat tutkimuksen koeryhmän ja kontrollipuolikkaat kontrolliryhmän.
Aineisto
Oppilaiden osaamista mitattiin kolme kertaa identtisellä kynä–paperi-testillä. Alkumittaus toteutettiin ennen murtolukujaksoa. Tutkijana oli kiinnostavaa nähdä, mitä oppilaat ovat oppineet intervention aikana. Alkumittauksen tarkoituksena olikin lähinnä tunnistaa ne oppilaat, jotka hallitsivat jo jonkin verran murtolukuja ennen varsinaisen opetuksen alkua. Toinen mittaus toteutettiin heti interventiojakson päätyttyä. Koska on luultavaa, että juuri opiskeltu asia on hyvin hallussa, kun sitä tuoreeltaan kysytään, pidettiin vielä kolmas, viivästetty mittaus noin kaksi–kolme kuukautta intervention päättymisen jälkeen. Tällöin nähtiin se, mitä oppilaat olivat opetuksesta sisäistäneet. Tehtävät arvioitiin pääosin oikein (1p)–väärin (0p).
Alkumittauksen osaamisen perusteella jaettiin oppilaat kahteen ryhmään: heikkoihin (R_) ja keskitasoisiin tai taitaviin (R+). Jos oppilas oli saanut alkumittauksessa korkeintaan seitsemän pistettä neljästäkymmenestä, sijoitettiin hänet R_-ryhmään (n. 23% oppilaista). Seuraavat tehtävät toimivat joukon jakajina. Suluissa on ilmaistu se, kuinka monella prosentilla ryhmän oppilaista tehtävä meni väärin: 23 + 18 (30%), 123 – 89 (95%), kolmasosa kuvasta (65%), lukujen 500 ja 750 sijoittaminen lukusuoralle (56%) ja (70%). Tehtävät olivat 2. luokan matematiikan sisällöistä, joten näiden tehtävien olisi pitänyt jo sujua 3. luokan puolivälissä. Oppilaiden osaaminen oli siis luokkatasoon nähden heikkoa. Alkumittauksen kokonaispisteet vaihtelivat välillä 3–22,5, maksimipistemäärä oli 40. Alkumittauksen perusteella joukossa oli muutama oppilas, jotka hahmottivat jo aika hyvin murtolukujen suuruuksia, alkumittauksessa saivat jopa 22,5p. Ikävä kyllä nämä oppilaat olivat poissa jommaltakummalta jälkimmäiseltä mittauskerralta ja siten jäivät aineiston ulkopuolelle. Tutkimusluvat haettiin Turun yliopiston eettiseltä toimikunnalta, oppilaitosten rehtoreilta, kunnan opetuslautakunnalta tai vastaavalta, oppilaiden vanhemmilta ja oppilailta itseltään. Tutkimusaineisto koostui lopulta 188 oppilaan kolmen mittauskerran vastauksista.
Tulokset
Kun verrattiin mittaustuloksia eri mittauskerroilla, ei kokonaispistemäärässä havaittua eroa koe- ja kontrolliryhmän välillä. Eroja löytyi vasta kun tarkasteltiin tehtäviä teemoittain: murtolukujen suuruuteen liittyvät tehtävät ja murtolukujen laskutoimituksiin liittyvät tehtävät. Lisäksi verrattiin koe- ja kontrolliryhmien taitotasoja keskenään.
Koeryhmän oppilaat hallitsivat kontrolliryhmän oppilaita paremmin sellaiset suuruusvertailutehtävät, joissa luonnollisten lukujen ominaisuuksiin nojaaminen ohjaisi väärään vastaukseen. Esimerkiksi oppilas saattaisi virheellisesti päätellä, että 1/2 < 2/5 koska 1 < 2 ja 2 < 5. Alkumittauksessa tätä virhekäsitystä ei vielä havaittu kummassakaan ryhmässä, joten se oli muodostunut mittausten välillä useammalle kontrolliryhmän oppilaalle kuin koeryhmän oppilaalle.
Koeryhmän taitotason R_-oppilaat hallitsivat kontrolliryhmän R_-oppilaita paremmin murtolukuihin liittyvät laskutehtävät ja jopa saavuttivat kontrolliryhmän R+-oppilaat (Kuva 2), vaikka ajallisesti laskuharjoitteluun oli käytetty vähemmän aikaa kuin kontrolliryhmässä. Koeryhmän R_-oppilaat hyötyivät selvästi interventiosta. Kuvassa nähdään myös osaamisen taantuminen viivästetyssä mittauksessa kaikissa muissa ryhmissä paitsi kontrolliryhmä taitotason R_-oppilailla, joilla osaaminen oli hyvin vaatimatonta toisella mittauskerralla.
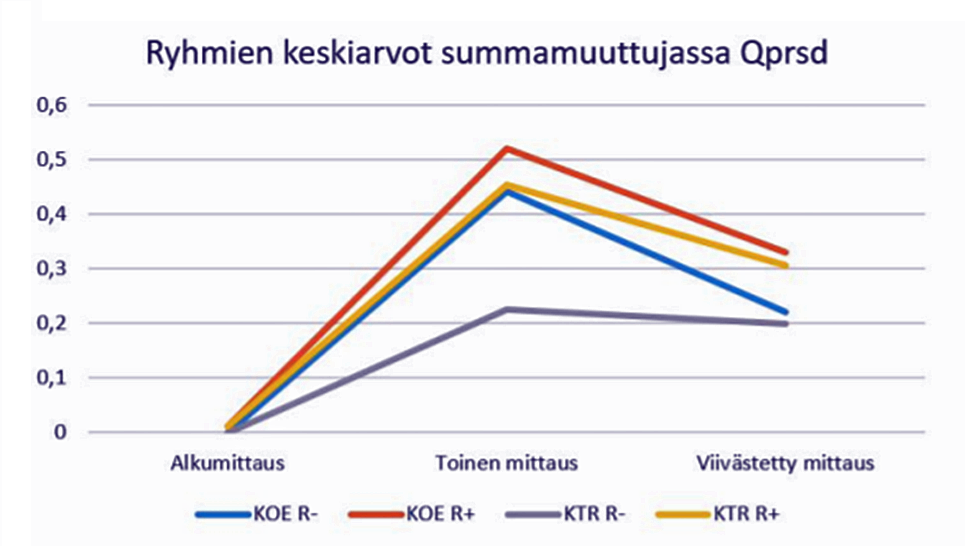
Koeryhmä oppitunneilla keskityttiin murtoluvun suuruuden ymmärtämiseen erilaisin välinein ja pelein. Tämä näyttäisi tukeneen oppilaita samannimisten murtolukujen yhteen- ja vähennyslaskutehtävissä.
Koe- ja kontrolliryhmän välillä ei kuitenkaan havaittu tilastollisesti merkitseviä eroja. Interventiossa käytetyt konkreettiset välineet, kuvallinen havainnollistaminen ja oppimispelit eivät siis ainakaan heikentäneet koeryhmän oppilaiden suoriutumista. Mielenkiintoista on se, että koeryhmän keskiarvot olivat useassa tehtävätyypissä hieman kontrolliryhmän tuloksia paremmat. Aina voidaan kuitenkin pohtia sattuman vaikutusta. Entäpä jos käännetäänkin asia toisin päin. Mikä on todennäköisyys sille, että neljästätoista tehtävästä kahdentoista tehtävän keskiarvo on koeryhmässä korkeampi kuin kontrolliryhmässä? Jos interventiolla ei ole mitään vaikutusta, tulisi olla yhtä todennäköistä, että jompikumpi ryhmä on toistaan parempi tai että eroa ei ole. Olkoon P(koe > ktr) = P(ktr > koe) = P(koe = ktr) = 1/3, silloin todennäköisyys sille, että koeryhmän keskiarvo on korkeampi kahdessatoista tehtävässä neljästätoista on P(koe > ktr) = 1412·0,33312·0,6672 ≈ 0,000076. Todennäköisyys pelkälle sattumalle on siis melkoisen pieni.
Yhteenveto
Vain viiden oppitunnin mittaisella painotuksen muutoksella saatiin aikaiseksi parempia oppimistuloksia erityisesti taitotasoltaan heikompien oppilaiden kohdalla. Koeryhmän oppilailla oli vähemmän havaittavissa tyypillistä virhekäsitystä (NNB) kuin kontrolliryhmän oppilailla. Huimin tulos on siinä, että matematiikkaa heikommin osaavat oppilaat saivat opetuksesta irti ja oppivat uuden asian, samannimisten murtolukujen yhteen- ja vähennyslaskun, kontrolliryhmän heikkoja oppilaita paremmin. Interventio osui siis maaliinsa.
Olisiko konkreettisista murtokakkupaloista iloa yläkoulussa?
Yläkoululaisetkin hyötyisivät murtokakkupalojen avulla murtolukujen peruslaskutoimitusten kertaamisesta heti 7. luokan alussa. Oppilaat saattavat aluksi karsastaa opetusvälinettä, sillä opetusvälineiden käytöstä on saattanut tulla alakoulun puolella leimaavaa. Harva murrosikäinen haluaa erottua massasta. Jos annetaankin opetusväline kaikille ja mallinnetaan laskutehtävät ensin välinein ja sitten kirjoitetaan vastaus symbolimuodossa, niin silloin opetusvälineen käyttö on yhteinen juttu. Taitavammille oppilaille voi antaa välineiden kanssa myös haastavampia tehtäviä kuten 1/3 : 1/2.
Osa oppilaista saa opetuksesta enemmän irti kuin toiset, koska oppilaat kehittyvät eri aikoihin. On helppo havaita että ”Simo on venähtänyt kesän aikana 10 cm” mutta sitä ei kukaan näe kuinka paljon ”Simon” abstraktiajattelu on kehittynyt kesän aikana. Suurin osa alle 12-vuotiaista on vielä konkreettisten operaatioiden vaiheessa ja siten he hyötyvät opetusvälineiden käytöstä. Matematiikan oppikirjoissa opetusta tukevat havainnollistavat kuvat vähenevät nopeasti, kun siirrytään 4., 5. ja 6. luokan oppikirjoihin. Jos opetus on pelkästään numerosymboleilla operoimista, on suuri riski, että oppilas ei saa opetuksesta irti vaan opettelee laskusääntöjä ulkoa, ymmärtämättä. Tavoitteena olisi kuitenkin synnyttää kestävää oppimista, jolloin opittua pystyttäisiin hyödyntämään myös myöhemmin. Ne oppilaat, jotka ovat jo ajattelussaan pidemmällä, pystyvät luomaan murtoluvista mielikuvia ja siten pärjäävät pelkkien symbolienkin kanssa.
Murtolukujen peruslaskutoimitusten opettamisessa käsitteet osoittaja ja nimittäjä ovat alakoulun matematiikan oppikirjoissa suuressa roolissa, vaikka huomio pitäisikin kiinnittää koko murtolukuun, ei pelkästään sen komponentteihin. Murtokakkupaloilla mallintamalla murtoluvun suuruus on koko ajan oppilaan silmien edessä. Opetusvälineitä hyödyntämällä taitotasoltaan heikommat oppilaat ja myös maahanmuuttajataustaiset oppilaat saattavat viimein oivaltaa, mistä murtolukulaskuissa on kyse. Esimerkiksi käsitteet laventaminen ja supistaminen saattavat luoda virheellisen mielikuvan siitä, että murtoluvun suuruus muuttuu. Murtokakkupalojen avulla on helppo todeta, että murtoluvun suuruus ei muutu, ainoastaan palojen koko ja lukumäärä muuttuvat.
Suosittelen vahvasti konkreettisten välineiden käyttöä koko peruskoulun ajan.
Väitöskirja on julkaistu sähköisesti ja se on ladattavissa osoitteesta https://www.utupub.fi/handle/10024/151563 Liitteenä löytyy myös tutkimuksessa käytetty mittari.
Aikaisempi murtolukujen oppimiseen liittyvä artikkeli Dimensiossa:
Tuominen, A. 2017. Murtolukujen peruslaskutoimitusten kehittyminen ja sujuminen 7. luokan aikana – 7.-luokkalaisten oppimisprofiilit. Dimensio, 1, 12–16.
Kirjoittaja Anu Tuominen, KT, FL, toimii yliopisto-opettajana Turun yliopiston opettajankoulutuslaitoksella opettaen tulevia luokanopettajia ja matemaattisen aineiden aineenopettajia.
Tilaa Dimension uutiskirje – saat sähköpostiisi aina kuunvaihteessa koosteen tuoreimmista artikkeleista
