Kaarileikkaus modernilla algebralla
Matematiikassa erityisesti kommutatiivisen algebran kehitys antaa uusia mahdollisuuksia lähestyä maanmittauksen ongelmia. Ohjelmistoihin tulleet työkalut helpottavat laskentaa oleellisesti ja ennen kaikkea ’vanhoihinkin’ ongelmiin saadaan uusi ratkaisutapa. Tässä kirjoituksessa käsitellään kaarileikkausta, mutta algebrallisia laskentamenetelmiä voidaan käyttää vaativimpiinkin geometrisiin ongelmiin.
Motivaatio tähän kirjoitukseen tuli siitä, että näitä algebrallisia menetelmiä voi käyttää yhtä hyvin niin kaksiulotteisen kuin useampiulotteisienkin avaruuksien tehtävien ratkaisuissa. Esimerkiksi GPS‐vastaanottimella saatu ratkaisu voidaan saada kohdasta, jossa neljän etäisyysfunktion arvot tulevat samoiksi. Nyt kun laseretäisyysmittareiden hinnat ovat halvenneet, niin voidaan näitä etäisyysmittareita käyttää tarkassa sijainnin määrittämisessä. Esimerkiksi laseretäisyysmittarilla pystytään saamaan paikan koordinaatit varsin helposti mittaamalla matkoja tunnettuihin pisteisiin. Silloin määritetään pisteen koordinaatit käyttämällä kaarileikkausta tai taaksepäin leikkausta; tietysti tehtävän geometria huomioon ottaen. Ylipäätään olkoonpa kysymyksessä mikä tahansa epälineaarinen yhtälö tai yhtälöryhmä, niin tulos saadaan ilman mitään alkuarvoa ja iterointia (mikäli ratkaisu on olemassa); tämä tekee Gröbner‐kannan avulla saadusta ratkaisusta mielenkiintoisen.
Geodesiassa ja geoinformatiikassa havainnot kuvataan usein epälineaarisilla yhtälöillä, joiden tuntemattomat parametrit ratkaistaan. Erityisesti pyritään siihen, että havainnoissa on riittävästi ylimääritystä ja sitten tasoituslaskennan avulla ratkaistaan parametrien todennäköisimmät arvot. Koska funktiot ovat epälineaarisia, pitää perinteisessä menettelyssä antaa alkuarvo ja aloittaa funktion lineaarisointi, minkä jälkeen alkuarvoa sitten lähdetään tarkentamaan seuraavilla iterointikierroksilla. Lineaaristen yhtälöiden tapauksessa on helppo antaa alkuarvoksi 0, mutta epälineaaristen tapausten kohdalla menettely on hankalampi. Aina lähtöarvo tai ’arvaus’ ei mene tarpeeksi lähelle ja iteraatio ei suppene vaan hajaantuu, jolloin tietysti ratkaisua ei saada.
Toinen syy on yleisempi ‐ David Cox, John Little ja Donal O’Shea sanovat kirjansa Ideals, Varieties, and Algorithms esipuheessa 1980–90‐lukuja pieneksi vallankumoukseksi kommutatiivisen algebran osalta (toinen painos vuodelta 1997). Polynomien joukko muodostaa kommutatiivisen algebran, kun se varustetaan normaalilla yhteen‐ ja kertolaskulla. Algebrallisen geometrian voima on siinä, että geometriset ongelmat voidaan kääntää abstraktin algebran probleemoiksi (Kahanpää, L., Smith, E.K., Kekäläinen. P., 2000). En ole nähnyt vielä suomenkielisiä maanmittaukseen sovellettuja kirjoituksia modernin algebran osalta.
Algebrallinen geometria tutkii polynomiyhtälöiden määrittelemiä geometrisia objekteja. Kommutatiivinen algebra taas on kommutatiivisten renkaiden teoriaa. Sillä on tärkeä merkitys algebrallisessa geometriassa, missä kommutatiiviset renkaat esiintyvät algebrallisten monistojen koordinaattirenkaina. Algebrallinen geometria on yksi modernin matematiikan keskeisistä osa‐alueista. Se on kuitenkin samalla erittäin klassinen matematiikan ala, jonka juuret juontavat Rene Descartesin (1596–1650) keksintöön esittää käyriä ja pintoja koordinaattien avulla. Algebrallisen geometrian sovellukset ulottuvat teoreettisesta fysiikasta informaatioteknologiaan. Viimeisen parinkymmenen vuoden aikana nimenomaan sovellukset koodausteoriaan ja kryptografiaan ovat herättäneet erityistä huomiota.
Algebraan liittyviä määritelmiä
Käsitteet kunta, rengas ja ideaali tulivat matematiikkaan saksalaisten Eduard Kummerin (1810–1893), Leopold Kroneckerin (1823–1891) ja Richard Dedekindin (1831–1916) algebrallista lukuteoriaa koskevien tutkimusten myötä. Kunta tosin oli implisiittisesti läsnä jo Evariste Galois’n (1811–1832) tarkasteluissa. Abstraktin aksiomaattisen määritelmän nämä struktuurit saivat vasta 1900-luvulla.
Algebrallinen ratkaisu vaatii hieman taustatietoja modernista algebrasta, erityisesti kunnista, renkaista, ideaaleista ja ryhmistä.
Polynomi
Matematiikassa polynomi on lauseke, joka saadaan yhdestä tai useammasta muuttujasta ja vakioista yhteen-, vähennys- ja jakolaskun sekä positiivisen kokonaislukueksponentin osoittamaan potenssiin korottamisella. Esimerkiksi x2 – 6x + 9 on polynomi. Polynomin, jonka aste on n, anxn + an-1xn-1 +…+ a1x + a0 johtava termi on se, jonka asteluku on suurin eli tässä lausekkeessa anxn. Yhdestä termistä koostuva polynomi on monomi, kahdesta binomi ja kolmesta trinomi. Esimerkiksi x, 3xy ja x2 ovat monomeja.
Kunta
Käsitteellä “kunta” on matemaatikoille erityinen merkitys. Alkioiden joukko muodostaa kunnan, jos alkioita voidaan laskea yhteen, vähentää toisistaan, kertoa ja jakaa normaalien laskusääntöjen mukaan. Laskutoimitusten tulosten on pysyttävä kunnassa. Kolmikkoa (K,+,⋅ ) on kunta, jos se täyttää seuraavat ehdot:
- Kaikilla x, y on x + (y + z) = (x + y) + z (summan liitäntälaki)
- Kunnassa K on nolla-alkio 0 niin, että kaikilla x on x + 0 = x (summan neutraalialkio)
- Kaikilla x on kunnassa K vasta-alkio –x siten, että x + (– x) = 0
- Kaikilla x, y on x + y = y + x (summan vaihdantalaki)
- Kaikilla x, y on x(y + z) = xy + xz (osittelulaki)
- Kaikilla x, y, z on x(yz) = (xy)z (tulon liitäntälaki)
- Kunnassa K on ykkösalkio 1 siten, että kaikilla x on 1 ⋅ x = x (tulon neutraalialkio)
- Kaikilla x, paitsi alkiolla 0, on kunnassa K käänteisalkio siten, että x ⋅ x-1 = 1 (tulon käänteisalkio)
- Kaikilla x, y on xy = yx (tulon vaihdantalaki)
Vaikka nimitykset (yhteenlasku, kertolasku, summa, tulo) antavat mielikuvan, että kunnassa pelataan luvuilla, niin näin ei välttämättä ole alkiot voivat olla muitakin käsitteitä kuin lukuja. Nollalla merkityn alkion 0 ei senkään tarvitse olla oikea nolla, vaan se on vain yhteenlaskussa vaikuttamaton alkio (yhteenlaskun neutraalialkio); samoin on ykkösellä merkitty 1 vain kertolaskussa vaikuttamaton alkio (kertolaskun neutraalialkio). Nämä yhdeksän ominaisuutta ovat juuri ne, jotka tunnetusti esiintyvät luvuilla. Tuntemamme tavalliset luvut, vaikkapa kaikki lukusuoran reaaliluvut, muodostavat siis kunnan. Reaalilukujen kunta on oikeastaan täydellinen järjestetty kunta.
Muita esimerkkejä kunnista ovat kompleksilukujen kunta sekä kaikki tämän alikunnat, joita nimitetään lukukunniksi. Näitä ovat muun muassa rationaalilukujen kunta Q, reaalilukujen kunta R, algebralliset lukukunnat K. Algebrallinen luku (reaali- tai kompleksiluku) on yhden muuttujan kokonaislukukertoimisen polynomiyhtälön nollakohta. Jos algebrallisesta luvusta μ ja rationaaliluvuista muodostetaan kaikki mahdolliset lausekkeet käyttäen peruslaskutoimituksia, niin tuloksena saatavat luvut muodostavat erään lukukunnan, algebrallisen lukukunnan K. Algebrallinen lukukunta sisältyy tai ei sisälly reaalilukujen kuntaan R sen mukaan, onko μ reaaliluku vai ei. Jos K on mielivaltainen kunta, niin kaikki sen alkioiden avulla muodostetut yhden tai useamman muuttujan rationaalifunktiot (polynomien osamäärät) muodostavat kunnan, niin sanotun rationaalifunktiokunnan. Tällainen voidaan puolestaan laajentaa esimerkiksi algebralliseksi funktiokunnaksi.
Rengas
Rengas on keskeinen algebrassa käytetty matemaattinen käsite, joka sijoittuu rakenteellisesti ryhmän ja kunnan väliin. Rengas sisältää kaksi laskutoimitusta: yhteen- ja kertolaskun. Yhteenlaskun suhteen se on Abelin ryhmä. Kertolaskun suhteen ryhmällä on olemassa neutraalialkio ja voimassa liitäntä- ja osittelulait. Sen sijaan renkaan alkioilla ei ole olemassa käänteisalkiota kertolaskun suhteen. Tämä ominaisuus liitetään kuntaan.
Ideaali
Kaikkien muuttujien x1, …, xn avulla lausuttujen polynomien, joiden kertoimet ovat kunnassa k, muodostamasta joukosta käytetään merkintää k[x1, …, xn] . (Cox, D.,Little, J.,O’Shea, D., 1997, s. 2)
Ideaali määritellään seuraavasti:
I ⊂ k[x1,…,xn] ideaali, jos
a) 0 ∈ I
b) jos f, g ∈ I, niin f + g ∈ I
c) jos f ∈ I ja h ∈ k[x1,…,xn], niin hf ∈ I.
Ideaalin I nollakohtien joukkoa (affine varieties) merkitään V(I): V(I) = {x∈kn ∣ f(x) = 0, ∀f ∈ I}. (Cox, D.,Little, J.,O’Shea, D., 1997)
Leksikograafinen järjestys
Polynomin esitysjärjestys vaikuttaa ratkaisuun – tässä artikkelissa käytetään ns. leksikograafista järjestystä. Useamman muuttujan x1,…,xn polynomin termit järjestetään leksikograafiseen järjestykseen seuraavalla tavalla:
- Verrataan ensin muuttujan x1 eksponenttia: jos niissä on eroa, niin suurimman eksponentin termi tulee leksikograafisessa järjestyksessä ensin
- Mikäli eroa ei tullut muuttujan x1 kohdalla, verrataan samoin muuttujan x2 eksponentteja
- Elleivät muuttjan xn eksponentin kertoimetkaan eroa toisistaan, termit ovat (vakiokerrointavaille) samat ja sijoittuvat leksikograafisessa järjestyksessä samalle kohtaa.
Leksikograafinen järjestys > lex on siis monomijärjestys, eli täysi hyvä järjestys, jolle pätee, että jos a < b, niin ac > bc, kun a, b ja c ovat mitä tahansa monomeja. Muitakin monomijärjestyksiä on ja polynomijoukolle laskettava Gröbnerin kanta riippuu siitä, mikä monomijärjestys valitaan. Tässä tapauksessa merkki > “suurempi kuin” ei merkitse numeerista suuruutta – sitä luonnehtii paremmin sanonta “a on ennen monomia b” tai “a on monimutkaisempi kuin b”.
Gröbner-kanta
Gröbner-kanta on yleistys Gaussin eliminointimenetelmästä eli toisin sanoen yleistys:
- lineaaristen yhtälöiden ratkaisumenetelmistä,
- Eukleideen algoritmista, jossa haetaan kahden polynomin suurin yhteinen jaettava
- lineaarisesta optimoinnista.
Tämä ratkaisu vaatii ohjelmistoa, jossa on Gröbner- kannan laskenta ohjelmoituna. Laskenta on tehty MAPLE:lla; muissakin ohjelmistoissa Gröbner-kanta on olemassa, esimerkiksi MATHEMATICA:ssa ja MAXIMA:ssa. Gröbner-kannan laskennan algoritmin kehitti Bruno Buchberger, joka toimii Itävallassa Linzissä Johannes Kepler yliopistossa symbolisen laskennan professorina.
Joukko {v1,…,vn} on lineaariavaruuden V kanta, jos jokainen avaruuden V alkio v voidaan esittää yksikäsitteisesti muodossa a1v1+. . . + anvn. Joukko G = {g1,…,gn} useamman muuttujan polynomeja puolestaan on Gröbner-kanta, jos jokainen näiden muuttujien polynomi on lausuttavissa muodossa a1g1 +. . . + angn + r, missä kertoimet ai ovat polynomeja ja jakojäännös r on yksikäsitteinen. G on polynomijoukkoa F = {f1,…,fn} vastaava Gröbner-kanta, jos polynomin fi yhteiset nollakohdat ovat samat kuin polynomin gi yhteiset nollakohdat.
Gröbner-kantoja voidaan muodostaa ns. Buchbergerin algoritmilla. Se muistuttaa yhden muuttajan polynomien jakojäännöksen laskemisalgoritmia, jossa jaettava jaetaan jakajalla termi kerrallaan muuttujan alenevien potenssien mukaisessa järjestyksessä. Myös Buchbergerin algoritmia käytettäessä on tarpeen järjestää useamman muuttujan polynomien termit jollakin tavalla. Siihen on monia vaihtoehtoja.
Eräs vaihtoehto termien järjestämiseen on leksikograafinen järjestys. Sitä käyttäen muodostettu Gröbner-kanta G vastaa lineaarisen tapauksen yläkolmiomuotoa: Jos yhtälöryhmällä fi(xi,…,xn) = 0 on ratkaisuja, kannassa G on polynomi, jossa esiintyy vain muuttuja xn, jolloin xn voidaan ratkaista. Kannassa G on tällöin myös polynomi, jossa esiintyy vain muuttujat xn ja xn-1, joten myös xn-1 saadaan ratkaistua, kun siihen sijoitetaan edellä ratkaistu xn. Kaikki tuntemattomat saadaan tällä tavoin ratkaistua yksi kerrallaan.
Buchbergerin algoritmi
Buchbergerin algoritmi voidaan koodata MAPLE:lla seuraavasti:
input: F ={f1,…,fs}, missä fi ∈ K[x1,…,xn] ja F =< f1,…,fs >.
output: G = {g1,…,gt}, siten, että G on Gröbner-kanta, F =< G > ja F ⊂ G.
G : =F;
repeat
GV : G; //vanha G
t : =≠ GV; //GV: n alkioitten lukumäärä
for i = 1. . . t – 1 do
for j = 1 + 1. . . t do
p : S(gi, gj); //gi: n ja gj: n S-polynomi, gi, gj ∈ GV
r : = jakojäännös(p, GV);
if r ≠ 0 then
G:=G∪{r};
end if
end for
end for
until G = GV.
Kaarileikkaus
Maanmittaus-lehdessä vuodelta 1953 on Reino Antero Hirvosen (1908–1989) artikkeli kaarileikkauksesta (Hirvonen, R.A., 1953). Kaarileikkaushan on kyseessä silloin, kun tunnetaan kaksi pistettä ja tuntemattomalta pisteeltä on tehty etäisyyshavainnot tunnettuihin pisteisiin. Matemaattisesti ratkaisuja on kaksi, mutta oikeassa mittaustilanteessa tiedetään, kummalle puolelle tunnettua janaa ratkaisu tulee. Kaarileikkauksen käyttö lienee tavallisinta silloin kun, jono-, monikulmio- tai kolmiopistettä joutuu etsimään sidemittojen tai varamerkkien avulla. Silloin kun Hirvonen on kaarileikkausesimerkin kirjoittanut, runkopisteitä oli harvassa ja uusia runkopisteitä piti perustaa silloisella mittaus- ja laskentatekniikalla.
Tässä on siis kyseessä tasolla tehtävä kaarileikkaus. Professori Hirvonen kehitti ratkaisua siihen suuntaan, että se on helposti laskettavissa joko käsin tai laskukoneella. Tämän päivän tietokoneet pystyvät käsittelemään isoja datamääriä eikä muistin koko enää ole niin iso ongelma kuin menneinä vuosina. Myöskin nykyisten tietokoneiden laskentatarkkuus on parantunut huimasti. Algebrallinen ratkaisu Gröbner-kannan avulla vaatii tietokoneen käyttöä, sillä polynomit, joiden avulla ratkaisu saadaan, tulevat kohtuullisen pitkiksi. Algebrallisessa ratkaisussa tarvitaan tietokoneelta prosessointitehoa. Toisaalta voi myös sanoa, että algebrallisessa ratkaisussa työ siirretään tietokoneen tehtäväksi, kun geometrinen ratkaisu perustuu enemmän laskijan ajatteluun.
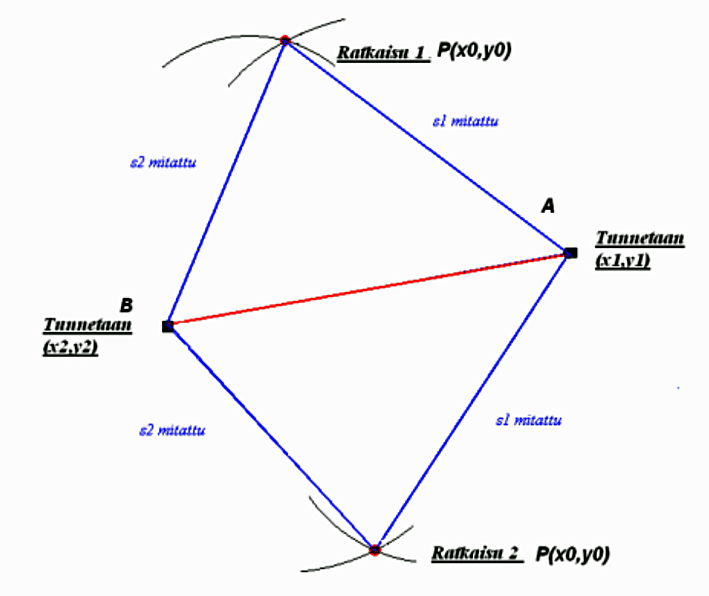
peilikuvana tunnetun janan AB suhteen.
1) Tavallinen ratkaisu
Perinteinen ratkaisu saadaan muodostamalla kaksi ympyrän yhtälöä ja ratkaisu on näiden ympyröiden leikkauspisteissä. Saadaan siis yhtälöt:
(x1 – x0)2 + (y1 – y0)2 = s12 ja (x2 – x0)2 + (y2 – y0)2 = s22
Kun sulkulausekkeet avataan ja siirretään säteet vasemmalle puolelle, saadaan:
x12 – 2x1x0 + x02 + y12 – 2y1y0 + y02 – s12 = 0 ja x22 – 2x2x0 + x02 + y22 – 2y2y0 + y02 – s22 = 0
Tästä voidaan ratkaista esimerkiksi y0, kun vähennetään ylemmästä alempi yhtälö.
$y_0=\{\frac{x_1-x_2}{y_2-y_1 }\}\ x_0+\frac{s_1^2-s_2^2+x_1^2-x_2^2+y_2^2-y_1^2}{2(y_1-y_2)}$
Sitten sijoitetaan saatu y0 jompaan kumpaan ympyrän yhtälöön, jolloin saadaan toisen asteen yhtälö, joka on ratkaistavissa. Tällä tavalla saatu ratkaisu on työläs. Matematiikkaohjelmistolla, kuten esimerkiksi MAPLE:lla, molemmat ratkaisut saadaan helposti. Täytyy vain tietää ympyrän yhtälön muoto, syöttää lähtötiedot ja ratkaisu on nopeasti saatu. Ensin annetaan lähtötiedot:
> x[1]:=3028.62;
> y[1]:=8458.53;
> x[2]:=2086.14;
> y[2]:=3117.82;
> s[1]:=4712.39;
> s[2]:=4084.07;
ja sitten kirjoitetaan yhtälöt:
>eqns:={(3028.62-x[0])^2+(8458.53-y[0])^2-22206619.51=0,(2086.14-x[0])^2+(3117.82-y[0])^2-16679627.76=0};
Ratkaisu saadaan komennolla solve:
>soln:=solve(eqns,{x[0],y[0]});
ja ympyröiden leikkauspisteiden koordinaateiksi tulee:
soln:= {y[0] = 4688.615714, x[0] = 5856.050952}, {y[0] = 5884.109567, x[0] = ‐918.4015280}.
2) Muut ratkaisut
Ongelma voidaan ratkaista myös muulla tavalla. Olen laskenut ratkaisun ongelmaan Hirvosen algoritmilla, Sylvesterin determinantilla ja Gröbner-kannan avulla. Tarkempi tutustuminen eri menetelmiin jätetään lukijalle. Tässä on tulokset.
- Hirvosen ratkaisu: Ratkaisu 1:x0=5856.05, y0=4688.62, ratkaisu 2:x0=‐918.40, y0 =5884.11. (Huom. Tätä ratkaisua 2 ei ole esitetty Hirvosen artikkelissa.)
- Ratkaisu Sylvesterin determinantilla: {x[0] = 5856.050953},{y[0] = 4688.615714} ja {x[0] = ‐918.4015304},{y[0] = 5884.109566}.
- Ratkaisu Gröbner‐kannan avulla: {x[0] = 5856.050871, y[0]=4688.615728} ja {x[0] = ‐918.4014462, y[0] = 5884.109552}.
Kiitokset matematiikan professori Antti Rasilalle, matematiikan emeritus lehtori Simo Kivelälle, matematiikan emeritus yliopettajalle Veikko Keräselle, maanmittauksen emeritus yliopettajalle Pasi Laurilalle, FM Lauri Laitiselle ja geodesian emeritus professori Martin Vermeerille. Heiltä olen saanut arvokkaita neuvoja artikkelin teon aikana. Opettajani Martin Vermeer kehotti aikoinaan LYX-ladontaohjelman käyttöön matemaattisessa artikkelissa. Se osoittautui hyväksi ratkaisuksi. Mahdolliset virheet ovat kuitenkin omiani.
Lähteet
Adams W.W., Loustaunau, P., 1994. An Introduction to Gröbner Bases. Graduate Studies in Mathematics.
Awange, J.L., Grafarend E.W. 2004. Solving Algebraic Computational Problems in Geodesy and Geoinformatics. The Answer to Modern Challenges. Springer.
Bingham, Kendrick, 1996. Polynomiyhtälöryhmän ratkaisemisesta Groebner-kantojen avulla. Numeerisen ja symbolisen laskennan kurssin harjoitustyö. http://math.tkk.fi/~kenny/opi/numsym/groebner/
Boyer C., Merzbach, U.C., Suomentanut K. Pietiläinen, 1994. Tieteiden kuningatar, Matematiikan historia osa II. Art House, WSOY.
[4] Cox, D.,Little, J.,O’Shea, D., 1997. Ideals, Varieties and Algorithms. An Introduction to Computational Algebraic Geometry and Commutative Algebra. Second Edition. Springer.
Derbyshire, J. Suomentanut J. Pietiläinen, 2006. Alkulukujen lumoissa. Terra Cognita.
Gander, W., Hřebíček, J., 1997. Solving Problems in Scientific Computing Using Maple and Matlab. Third Edition. Springer.
Gatermann, K., 1980. Computer Algebra Methods for Equivariant Dynamical Systems. Lecture Notes in Mathematics. Springer.
Hilbert D., Translated by Laubenbacher R.C, edited by Laubenbacher R.C. and Sturmfels B., 1994. Theory of Algebraic Invariants. Cambridge University Press.
Hirvonen, R.A., 1953. Kaarileikkaus. Artikkeli Maanmittaus-lehdessä. Kahanpää, L., Smith, E.K., Kekäläinen. P., 2000. Johdattelua algebralliseen geometriaan. Otatieto.
Lehtinen, M.,Merikoski, J.,Tossavainen, T., 2007. Johdatus tasogeometriaan. WSOY Oppimateriaalit Oy.
Metsänkylä, T., Näätänen M., 2005. Algebra. 2. korjattu painos. Limes ry.
Sturmfels, B., 2008. Algorithms in Invariant Theory. Second Edition. Springer.
Wikipedia: Arthur Cayley. http://en.wikipedia.org/wiki/Arthur_Cayley







