Kohti kielitietoisuutta – kielen ja matematiikan oppimisen kytkökset

Joka oppiaineella on oma kielensä, mutta matematiikan oppimisessa ja osaamisessa tarvitaan jopa neljää eri kieltä. Niiden opettamisessa opettajan kielitietoisuus on ydinasia. Ymmärrys oppimisen ja kielen yhteyksistä auttaa opettajaa tekemään opetuksessaan kielitietoisia valintoja.

Oppiaineesta riippumatta lähtökohta on se, että koulun toiminnassa ja oppimisessa keskeistä on kieli. Tämä tarkoittaa sitä, että sisältöä ja kieltä ei voi erottaa toisistaan. Käytännössä se näkyy siinä, että jokainen aineenopettaja on oman aineensa kielenopettaja, joka avaa käsitteitä, selittää ja selventää. Opettaja siis opettaa sisältöä niin, että kieli tukee sisällön oppimista – ei estä sitä. Tätä voi hyvällä syyllä kutsua opettajan pedagogiseksi vastuuksi. 

Nykykoulussa on monikielisiä oppijoita ja monia äidinkieliä. Yksi puoli kielitietoisuutta on kaikkien kielien arvostus ja ymmärrys kunkin äidinkielen keskeisestä merkityksestä. Opettajan tulee tukea tasa-arvoa, ja opettajan työhön kuuluu asenneilmapiirin luominen: kielitietoinen opettaja haluaa parantaa oppijoiden osallisuutta ja mahdollisuuksia oppia. Se koskee kaikkia eli äidinkieleltään suomenkielisiä oppijoita, oppijoita, joilla on erilaisia oppimisvaikeuksia ja suomi toisena kielenä -oppijoita.

Mitä opettajan pitää tietää kielestä?

Missä muodoissa kieli on mukana? Matematiikan tunneilla oppija lukee oppikirjan tekstejä ja tehtäviä, opettajan materiaaleja ja tehtäväksi antoja, kuvioita, kuvia, taulukoita ja kaavioita. Hän tuottaa niitä myös itse, hän esimerkiksi kirjoittaa symbolein laskutoimituksia. Hän kuuntelee opettajan ja ryhmäläisten matemaattista puhetta sekä puhuu sitä itse ja keskustelee niin, että käyttää matematiikan sanastoa ja käsitteistöä. Hän ratkaisee sanallisia tehtäviä, sanallistaa ratkaisujaan ja perustelee valintojaan. 

Usein voi vaikuttaa siltä, että oppija osaa arkikieltä aika hyvin. Se ei vielä kerro sitä, miten hyvin hän hallitsee oppiaineen kielen, joka on ammattikieltä eli käsitteitä ja erikoissanastoa sekä alan tekstirakenteita. Ne täytyy erikseen oppia, ja siinä prosessissa aineenopettaja on kielenkäytön malli.

Opettajan työtä on seuloa, mitä matematiikan käsitteitä oppijan täytyy osata. Seuraavaksi opettajan on ratkaistava, miten hän varmistaa, että oppija oppii uudet käsitteet. Matematiikan kielessä ja teksteissä on lisäksi toistuvia rakenteita, joten niiden tunnistaminen on tärkeää: opettajan on kielellistettävä ne, jotta oppijat oppivat tunnistamaan ne opetusmateriaaleista ja tehtävistä sekä käyttämään niitä itse.

Ylipäätään matematiikan kieliä on monta, ja ne ovat oppijalle uusia kieliä, jotka täytyy oppia ja osata. Se vaatii siis kaikilta vaivaa ja kärsivällisyyttä. Opettajan tulisi antaa oppijoille aikaa prosessoida uusia symboleita, käsitteitä ja tekstirakenteita. Oppija joutuu kääntämään niitä omalle äidinkielelleen (arkisuomeksi tai muuksi äidinkieleksi) sekä ymmärtämään uusia käsitteitä merkityksineen, ja se vaatii prosessointiaikaa. Myös keskustelulle tulisi olla aikaa, sillä merkitykset rakentuvat usein vuorovaikutuksessa muiden kanssa.

Outo kieli oppijalle

Matematiikan käsitteet ja sanasto ovat oppijalle outoja, uusia ja vieraita tai niillä on eri merkityksiä “eri kielissä”, esimerkiksi arkikielessä kanta ja tahko ovat ihan eri asia matematiikassa kuin arkikielessä. Lisäksi monet käsitteet ovat pitkiä ja monimutkaisia, vaikka ne yrittävät olla yksiselitteisiä. Matematiikan oppijalle ne ovat kuitenkin vaikeita ymmärtää, kuten ympyräpohjainen lieriö. 

Seuraavassa esimerkissä (oppikirja Kertoma 4) on vain muutama sana arkikieltä (alleviivattu teksti), muu on erikoissanastoa tai sanojen merkitys on eri kuin arkikielessä – esimerkissä on siis termejä ja käsitteitä, jotka täytyy erikseen oppia ja osata. Siksi teksti on vaikea ymmärtää, vaikka lauseet ja virkkeet ovat melko lyhyitä. Lisäksi passiivi hankaloittaa ymmärrettävyyttä:

”Funktion muutosnopeutta tietyssä pisteessä kutsutaan funktion derivaataksi. Geometrisesti derivaatta on pisteeseen piirretyn tangentin kulmakerroin. Derivaatta määrittelee funktion, jonka arvo tietyssä pisteessä kertoo funktion tangentin kulmakertoimen arvon. Funktion derivaatan arvoja saadaan laskettua algebrallisesti derivaattafunktion avulla.”

Opettajan strategia on käyttää helppoa ja konkreettista arkikieltä, jolla uusista merkityksistä tulee tuttuja. Se ei tarkoita tavoitteiden helpottamista vaan johdattelua uuden oppimiseen, mikä on välivaihe kohti käsitteiden ymmärtämistä ja käyttöä. 

Opettaja tekee havaintoja aineensa kielestä – puhuu niistä ääneen oppijoille, selittää ja selventää. Vain siten voi edetä arkikielestä ammattikielen oppimiseen. Kielitietoinen opettaja on valmis arvioimaan omaa kielenkäyttöään. Ydinkysymys on, kohtaako opettajan käyttämä kieli oppimistilanteissa oppijoiden kielen taidon tason.

Matematiikan kieliä onkin monta

Luonnollinen kieli, matemaattisten symbolien kieli, kuvioiden kieli ja taktiilisen toiminnan kieli ovat vuorovaikutuksessa keskenään. Näiden vuorovaikutuksesta rakentuu matemaattinen ymmärrys.

Unkarilaisessa Varga-Neményi-opetusmenetelmässä ja Montessori-kouluissa korostetaan sitä, että oppilas oppii ensin toiminnallisten välineiden avulla. Kun palikoita käsittelemällä on ymmärretty idea, se sanallistetaan luonnolliselle kielelle ja kirjoitetaan myös matematiikan symbolien kielellä.

Matematiikan opettamisessa on se ristiriita, että ihminen oppii ensin konkreettisista yksittäistapauksista, joista vähitellen päätellään yleinen sääntö. Mutta matematiikka perustuu abstrakteille yleisille säännöille, joista voidaan johtaa yksittäistapauksia. Matematiikan ideaalimaailmassa säännöt toimivat täydellisesti, ja hyväksytty epätarkkuus on tasan nolla. Oppilaiden konkreettisessa maailmassa viivoittimen reuna voi olla vääntynyt, harpin säädöt löystyneet ja punnukset pölykerroksen massan verran eri kokoisia keskenään. Piirroksissa täytyy hyväksyä vähintään lyijykynän viivan paksuuden verran epätarkkuutta.

Jos matematiikan opettaja on sisäistänyt liian hyvin puhtaan matematiikan kauneuden, hän ei voi hyväksyä sitä, että oppilaan mittaustuloksissa kolmion kulmien summa voi olla 179° tai 181°. Matemaatikon ammattitaito on sitä, että pystytään kuvittelemaan äärettömän ohuista janoista piirretty kolmio, jonka kulmien suuruuksia ei edes tarvitse mitata, koska ilman lukuarvojakin voidaan todistaa, että kulmien summa on tasan 180° – tai mieluummin 𝝅 radiaania. Opettajan ammattitaito on sitä, että opettaja saa oppilaan ymmärtämään, miten yhä tarkemmin ja tarkemmin tehdyt piirrokset ja mittaukset alkavat lähestyä oikeaa tulosta.

Matemaattisten symbolien kieltä täytyy oppia, koska se on tehokas työkalu ongelmien ratkaisemiseen. Matematiikka kehittyi kirjanpidon tarpeisiin: kuinka suuria tontteja ihmiset omistivat ja kuinka paljon veroja heidän täytyi maksaa? Negatiiviset luvut otettiin käyttöön kuvaamaan velkaa. Peruslaskutoimituksia yhdistelemällä voidaan rakentaa funktioita eli laskusääntöjä, jotka antavat tuloksena esimerkiksi taksimatkan hinnan ajettujen kilometrien perusteella, tai sähkölaskun kulutetun energian perusteella. Taloustieteessä tutkitaan funktioiden leikkauspisteitä ja nousukulmien jyrkkyyksiä. Jos hinnoittelussa voidaan ottaa keskiarvon laskemisen sijasta työkaluksi derivointi, se on suunnilleen samanlainen harppaus kuin puuseppä vaihtaisi taltan ja käsisahan CNC-jyrsimeen. Vaihtosähkön ja radioaaltojen toimintaa voidaan ymmärtää, koska on mahdollista laskea myös yli 90-asteisen tai alle 0-asteisen kulman sini. Arkijärjellä 181-asteisen kulman sinin ajatteleminen sattuu aivoihin yhtä paljon kuin imaginäärilukujen kuvitteleminen.

Monien ihmisten matematiikka-ahdistus on kehittynyt sen vuoksi, että he ovat epätoivoisesti yrittäneet opetella matematiikan symbolikieltä niin, että symbolit eivät ole linkittyneet konkreettiseen todellisuuteen eivätkä edes luonnollisen kielen todellisuuteen. Merkinnät ja laskutoimitukset eivät tarkoita heille mitään, ja niiden käsittelyn sääntöjä on ehkä opittu ulkoa, tai sitten ei. Jos oppilas laskee kirjahyllyyn mahtuvan akvaarion tilavuudeksi 60 000 000 litraa tai 0,06 metriä eikä väärä suuruusluokka tai väärä yksikkö soita hänen päässään hälytyskelloja, niin yhteys symbolien ja konkretian väliltä puuttuu. Laskuharjoituksiin tarvitaan avuksi ainakin litran mitta, ja mielellään myös ämpäri, kuutiometrin rautalankamalli ja akvaarion kokoinen laatikko.

Alakoululainenkin voi oppia, miten yhden käden sormilla lasketaan 31:een ja kahden käden sormilla 1023:een. Laskusäännön todistaminen jätetään harjoitustehtäväksi.

Havainnollistaminen auttaa ymmärtämään

Martta Hakamies on videoinut havainnollistamisesimerkkejä. Havainnollistamisesimerkit on tiivistetty tähän lukuun myös tekstin ja kuvien avulla.

Murtoluvut

Peruskoulun matematiikan opetuksessa ensimmäinen kompastuskivi ovat murtoluvut. Jos oppilas ei ymmärrä murtoluvun käsitettä, hän ei voi ymmärtää, miksi murtolukujen laskusäännöt toimivat niin kuin ne toimivat. Tyypillinen virhe erinimisten murtolukujen yhteen- ja vähennyslaskuissa paljastaa, että oppilas ei ole ymmärtänyt, miten murtoluvut toimivat: 

$$\frac{1}{3}+\frac{1}{2}=\frac{1+1}{3+2}=\frac{2}{5}$$

Miksi vastaus on väärin? Miksi näin ei voi laskea?

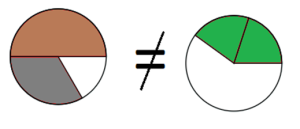
Murtokakkupalojen avulla oppilas voi todeta itse, että ⅓ + ½ ei ole sama asia kuin ⅖. Palojen avulla voidaan myös havaita, että laventaminen ei muuta murtolukua suuremmaksi eikä pienemmäksi.

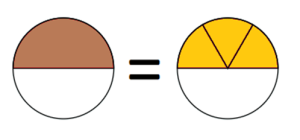
Oppilaan on helpompi oppia suorittamaan murtolukujen laskutoimitukset ensin palikoiden avulla. Palikoista voidaan vähitellen edetä piirroksiin ja sanallisiin selityksiin, ja lopuksi opitaan, miten samat laskutoimitukset kirjoitetaan matemaattisilla merkinnöillä.

Prosenttilaskut

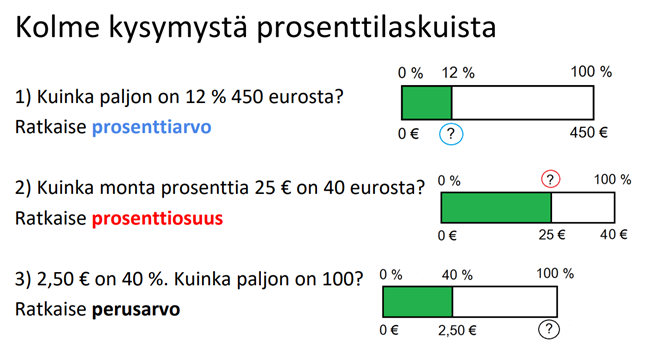
Jos murtoluvun käsite on jäänyt heikolle pohjalle, vaikeudet jatkuvat prosenttilaskujen kanssa. Prosenttilaskuista on olemassa vain kolme erilaista kysymystä, ja kysymystyypin tunnistaminen oikein auttaa jo pitkälle tehtävän ratkaisussa: onko tarkoituksena ratkaista prosenttiarvo, prosenttiosuus vai perusarvo? Erityisen vaikeissa prosenttilaskutehtävissä on yhdistelty kaikkia kolmea kysymystyyppiä, ja ratkaisun vaiheissa täytyy käyttää eri laskukaavoja oikeassa järjestyksessä.

Yhtälön tasapainottamiseen tarvitaan joskus antiainetta

Yhtälönratkaisun opetuksessa on perinteisesti käytetty vertauksena vaakaa, joka täytyy pitää tasapainossa. Vaa’an molemmille puolille täytyy tehdä samat toimenpiteet, jotta tasapaino säilyy. Jos yhdeltä puolelta otetaan pois jotain, mutta toiselta puolelta ei, ratkaisu on väärin, koska vaaka ei pysynyt tasapainossa.

Yhtälön $3x+2=2x+5$ havainnollistamiseen tarvitaan kahdenlaisia palikoita. Tässä kuvassa vihreät x-kirjaimet ovat tuntemattomia ja keltaiset ympyrät ovat ykkösiä.

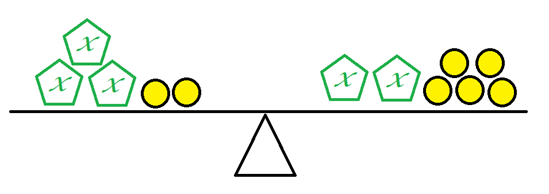
Yhtälöstä voidaan poistaa molemmilta puolilta 2x ja sitten 2, jolloin vasemmalle puolelle jää vain x ja oikealle puolelle jää 3.

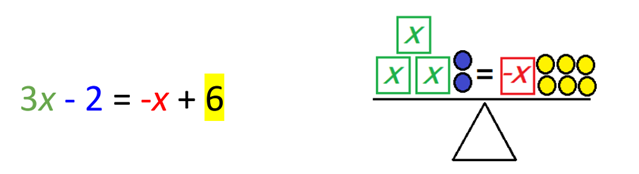
Jos yhtälössä esiintyy negatiivisia lukuja, tarvitaan myös antiaineesta tehtyjä palikoita. Yhtälön $3x-2= -x+6$ molemmille puolille täytyy lisätä $x+2$. Silloin $-x$ ja $-2$ annihiloituvat. Jos vaaka selviää räjähdyksestä ehjänä, se on edelleen tasapainossa, ja yhtälö on askeleen lähempänä ratkaisua.

Pinta-ala ja tilavuus

Pituuden, pinta-alan ja tilavuuden yksiköiden havainnollistaminen välineillä auttaa opiskelijoita ymmärtämään, milloin suhdeluku on 10, milloin 100 ja milloin 1000. Yhteen metriin mahtuu 10 desimetriä, joten yhteen neliömetriin mahtuu 10*10 neliödesimetriä, ja yhteen kuutiometriin mahtuu 10*10*10 kuutiodesimetriä.

Trigonometria on kolmion mittaamista

Mittaa kuvan kolmiosta kateetin $a$ pituus, hypotenuusan $c$ pituus ja kulman asteet. Laske $a/c$. Laske $sin(\alpha)$. Saitko samat tulokset?

Piirrä kolmioon yksi pystysuora viiva niin, että saat uuden, pienemmän kolmion. Mittaa uuden kolmion kateetti $a_2$ ja hypotenuusa $c_2$. Laske suhde $a_2/c_2$. Saitko saman tuloksen kuin aikaisemmin? Mitä tapahtuisi, jos piirtäisit kulman kylkiä vielä pidemmiksi ja piirtäisit kolmion ulkopuolelle uuden pystysuoran viivan $a_3$ niin, että saisit entistä suuremman kolmion?

Tämäkin tehtävä johdattelee oppilasta kohti matematiikan ideaalimaailmaa, mutta lähtee liikkeelle yksittäistapauksesta ja pölyisestä arkimaailmasta, jossa mittaustarkkuus ei ole täydellinen. Muutaman sadasosan ero vastauksissa on mahdollista selittää sillä, että jokin mittaustuloksista on puoli millimetriä liian paljon tai liian vähän. Jos vastauksissa on kymmenesosan ero, niin sitten on syytä harjoitella tekemään mittaukset tarkemmin.

Kielelliset valinnat opetuksessa

Kielitietoinen opettaja siis avaa käsitteitä ja rakenteita, selittää ja selventää, piirtää, näyttää kuvia sekä käyttää havainnollistavia esineitä ja tavaroita. Hän toistaa ja kertaa sekä varmistaa, että oppija on ymmärtänyt asian.

Opettaja tekee kaiken aikaa kielellisiä valintoja. Häntä auttaa, kun hän tietää helpon kielen periaatteita. Kielitietoisuus ei tarkoita sitä, että opettajan täytyy käyttää selkokieltä eli yleiskieltä helpompaa kieltä. Sen sijaan kielitietoisuutta on se, että opettaja tietää, mitkä asiat tekevät kielestä helppoa tai vaikeaa. Se saa opettajan tarkastelemaan opetuspuhetta, materiaaleja ja tehtäviä helpon, ymmärrettävän kielen kannalta. Toisaalta juuri silloin on hyötyä, jos opettaja tietää jotain selkokielen periaatteista: ne konkretisoivat, mitkä kielelliset valinnat helpottavat ymmärtämistä.

Mihin ennen kaikkea kannattaa kiinnittää huomiota? Ensinnäkin opettaja tekee sisällölliset valinnat vastaanottajan tietojen ja taitojen perusteella: oppija voi oppia uutta vain vanhan ja tutun tiedon päälle. Toisekseen uudet sanat, termit ja käsitteet oppija oppii vain, kun ne tulevat ymmärrettäviksi tutun, helpon kielen keinoin. Niitä täytyy toistaa ja käyttää apuna esimerkkejä, havainnollistamista ja toiminnallisuutta.

Sanonnat, kielikuvat ja ammattislangi vaikeuttavat ymmärtämistä. Pitkät yhdyssanat ovat vaikeita, samoin se, kun sanoja on johdettu. Silloin merkitysmuutos vaatii konkretisointia ja havainnollistamista, esimerkiksi miten laite ja laitteisto eroavat toisistaan? 

Suomen kielessä on paljon taivutusmuotoja, jotka vaikeuttavat ymmärtämistä. Kun opettaja tunnistaa ne ja kirjoittaa koetehtävät välttäen vaikeita kielen muotoja, koe mittaakin niitä taitoja, joita sen tulee mitata. Silloin ei jää arvioimatta osaava mutta tehtävineen hämmentynyt oppija, jonka osaaminen on tunnistamatonta opettajan kielivalintojen vuoksi. (Virkkeessä on alleviivattu vaikeita kielen muotoja. Helpon kielen ohjeita on Kieliteitoisen opettajan tarkistuslistassa, bit.ly/selkotarkistaMAOL.)

Hyvä kieli on yksiselitteistä ja selkeää. Jo se helpottaa ymmärtämistä ratkaisevasti, kun passiivimuoto muuttuu aktiivimuodoksi tai kun virke alkaa päälauseella eikä sivulauseella. Ymmärtämistä tukee myös se, kun kiellon sijasta oppija kuulee tai lukee, mitä täytyy tehdä. Ohjeiden ja tehtävien kuulija tai lukija tietää, mikä hän tekee, kun virkkeet ovat lyhyitä, kieli on helppoa ja vastaanottajaa “sinutellaan”. Vertaa vaikka:

Jos käytetään vaikeaa kieltä, tulee ohjeisiin väärinymmärryksiä. -> Käytä helppoa kieltä. Silloin oppija ymmärtää ohjeet oikein.

Lopuksi sopii tuoda esiin vielä yksi kielitietoisuuden keskeinen periaate: opettaja tekee yhteistyötä muiden opettajien kanssa. Yhteistyö esimerkiksi materiaalien ja tehtävien teossa hyödyttää monin tavoin, koska yhteinen pohdinta tehostaa havaintoja kielestä ja kielitietoisista käytännöistä. Samalla kehittyy työyhteisön jakamisen kulttuuri. Eri aineiden opettajat ovat myös hyvä kohderyhmä, jolla voi testata, onko opetusmateriaali ja ohjeistus ymmärrettävää. 

Artikkeli on osa Kielitietoisuus matematiikan opetuksessa -koulutushanketta, jonka rahoitti OPH. Hankkeessa luodut materiaalit MAOLin verkkosivuilla.

Lähteitä

Hakamies, M. 2022. Matemaattis-luonnontieteellinen osaaminen. OPH:n webinaarin diasarja. https://www.oph.fi/sites/default/files/documents/OPH-matlu-2022-03-31.pdf

Joutsenlahti, J. 2022. LUMATIKKA. Matemaattisen ajattelun kielentäminen. https://www.youtube.com/watch?v=T428kK6QulQ

Kartio, J. 2016. 12 askelta selkokielellä opettamiseen. Kansalaisopistojen liiton materiaaleja 1.https://blogs.helsinki.fi/vastaantulo/2017/09/28/paivi-portaankorva-koivisto-kielen-merkitys-matematiikan-kasitteiden-oppimisessa/

Leskelä, L. 2019. Selkokieli. Saavutettavan kielen opas. Helsinki: Opike.

Mitä on kielitietoisuus? 5.5.2021. Opetushallitus. Kielitietoisuus. https://www.oph.fi/fi/opettajille/kielitietoisuus

Monikielisen oppijan matkassa. Kielitietoinen opetus. 2022. https://monikielisenoppijanmatkassa.fi/kielitietoinen-opetus/

Opetushallitus. Kielitietoisuus. 2022. https://www.oph.fi/fi/opettajille/kielitietoisuus

Opetushallitus. Matematiikan päättöarviointi. Millainen on kielitietoinen matematiikan opettaja? 2022. https://www.oph.fi/fi/koulutus-ja-tutkinnot/matematiikan-paattoarviointi

Perkkilä, P. & Joutsenlahti, J. 20.1.2022. Matemaattisen ajattelun kielentäminen ymmärtävän oppimisen perustana. https://dimensiolehti.fi/matemaattisen-ajattelun-kielentaminen-ymmartavan-oppimisen-perustana

Portaankorva-Koivisto, P. 11.11.2020. LUMATIKKA-webinaari: Kielitietoisuus matematiikan opetuksessa. https://www.youtube.com/watch?v=lzZZaTgH288

Sainio, A. 2022. Avaimet selkokieleen. Opike.

Selkokeskus. Selkokieli. 2022. https://selkokeskus.fi/selkokieli/

Takala, T. (kokoaja). 2022. Kielitietoisen opettajan tarkistuslista. bit.ly/selkotarkistaMAOL; https://maol.fi/app/uploads/2022/09/Kielitietoisen-opettajan-tarkistuslista.pdf

Varga-Neményi ry. Todellisuuteen perustuvien kokemusten hankkiminen. 24.1.2016. https://varganemenyi.fi/menetelma/tietoa-menetelmasta/varga-nemenyi-menetelma/24-menetelman-osiot/36-todellisuuteen-perustuvien-kokemusten-hankkiminen

---

Vastaa Dimensio-lehden lukijakyselyyn 23.4.2023 mennessä ja voit voittaa kirjan Matematiikkaa huonoin piirroksin.