Ko­ke­muk­sia ma­te­ma­tiik­kao­lym­pia­lais­ten teh­tä­vis­tä 2021

Vuoden 2021 kansainväliset matematiikkaolympialaiset piti järjestää Pietarissa, mutta pandemiatilanteen vuoksi tapahtuma järjestettiin etänä. Suomessa tapahtuma järjestettiin Helsingissä, jossa kahden päivän kilpailua edelsi myös noin viikon pituinen valmennus.

Kuten aiempana vuonna, myös tänä vuonna kilpailu oli poikkeuksellisen tehtävänvalintaprosessinsa vuoksi hieman erikoinen. Esimerkiksi tehtävät kaksi ja kolme olivat hyvin vaikeita, ja kilpailussa ei juurikaan esiintynyt lukuteoriaa. Omasta mielestäni myös geometrian tehtävät olivat epätavallisia.

Itse sain tehtyä tehtävät yksi ja neljä: Ensimmäisen pienen virheen kera, sekä toisen kokonaan. Tässä on lähestymistapani ja pohdintani näistä kahdesta tehtävästä:

Tehtävä 1

Olkoon $n\ge 100$ kokonaisluku. Ivan kirjoittaa kunkin luvuista $n,n+1,\ldots,2n$ eri korteille. Sitten hän sekoittaa nämä $n+1$ korttia ja jakaa ne kahteen pinoon. Osoita, että vähintään yksi näistä pinoista sisältää jotkin kaksi korttia, joiden lukujen summa on neliöluku.

Minulle luonnollinen lähestymistapa oli ajatella ongelmaa verkkona, jossa solmut ovat positiivset kokonaisluvut $\{n,n+1,n+2,\ldots,2n\}$ ja kahta solmua $x$ ja $y$ yhdistää särmä, jos $x+y$ on neliö. Tällöin tehtävänä on näyttää, että verkko ei ole kaksijakoinen, eli sen solmuja ei voi värittää kahdella värillä niin, että kahta samanväristä solmua yhdistää särmä. Heti tämän jälkeen minulla oli kaksi ideaa tehtävän ratkaisemiseen: Globaali idea, eli kokonaiskuvaa tutkiva idea, ja lokaali idea, eli pientä kuvaa tutkiva idea.

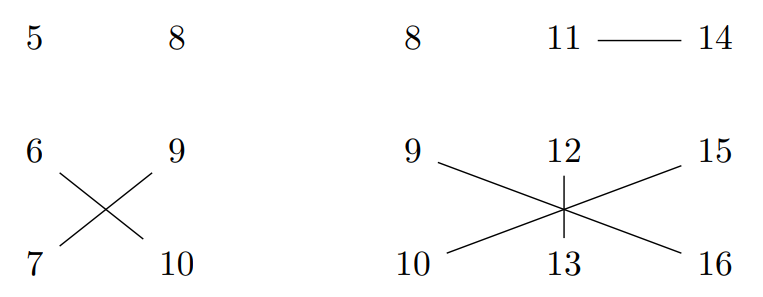
Selvästikin jos verkossa on ”liian monta” särmää, se ei voi olla kaksijakoinen. Siispä globaali idea oli todistaa, että konstruktoidussa verkossa on ”liian monta” särmää. Itse asiassa jos kaksijakoinen verkko on jaettu $a$ punaiseen ja $b$ siniseen solmuun, niin särmiä on korkeintaan $ab$. Lisäksi aritmeettis-geometrisen epäyhtälön nojalla tämä on korkeintaan $(a+b)^2/4=n^2/4$ Siispä ajattelin, että jos voin näyttää konstruktoidussa verkossa olevan ainakin $n^2/4$ särmää, niin se ei voi olla kaksijakoinen, ja olen valmis.

Tajusin kuitenkin aika nopeasti, että tämä idea ei toimi. Lukujen summat sijaitsevat välillä $[n+(n+1),(2n-1)+2n]=[2n+1,4n-1]$ ja tällä välillä on $\sqrt{4n-1}-\sqrt{2n}\le 2\sqrt{n}$ neliötä. Lisäksi jokaista tämän välin neliötä vastaa korkeintaan $n$ paria, joidenka summa on kyseinen neliö. Siispä verkossa on korkeintaan $2n^{3/2}$ särmää, joka on huomattavasti pienempi kuin $n^2/4$ tarpeeksi suurilla $n$. Oli siis aika siirtyä toiseen ideaan.

Lokaali idea oli löytää ristiriita suoraan. Tarkemmin, jos verkossa on olemassa kolmio, eli sellaiset solmut $x,y,z$, joilla jokaista kahta solmua yhdistää särmä, niin laatikkoperiaatteen nojalla verkko ei voi olla kaksijakoinen. Riittää siis löytää sellaiset erisuuret kokonaisluvut $x,y,z$ välillä $[1,n]$, joilla $x+y,y+z,z+x$ ovat kaikki neliöitä. Tämä edellyttää sellaisten kokonaislukujen $A,B,C$ olemassaolon, joilla $$\begin{cases}x+y=A^2\\ y+z=B^2\\ z+x=C^2\end{cases}\Leftrightarrow \begin{cases}x=(A^2-B^2+C^2)/2\\ y=(A^2+B^2-C^2)/2\\ z=(-A^2+B^2+C^2)/2 \end{cases}$$

Huomaa myös, että kaikki erisuuret kokonaisluvut $A,B,C$, joilla mainitut arvot ovat kokonaislukuja välillä $[n,2n]$, antaa kolmion muodostavat $x,y,z$. Tämä johtuu siitä, että $A,B,C$ erisuuruus tarkoittaa myös $x,y,z$ erisuuruutta. Riittää siis löytää sopivat $A,B,C$.

Tätä varten on luonnollista tutkia, jos joku peräkkäisten kokonaislukujen kolmikko toimisi. Tarkemmin, olkoon $(A,B,C)=(2k-1,2k,2k+1)$. Toteutuuko haluttu ehto jollakin kokonaisluvulla $k$? Vastaus on kyllä: Esimerkiksi on helppo tarkistaa, että arvolla $k=\lfloor\sqrt{n}\rfloor-1$, jossa $\lfloor x\rfloor$ meinaa suurinta kokonaislukua, joka on korkeintaan $x$. Siten olemme löytäneet sopivat $A,B,C$, ja vastaavasti kolmion muodostavat $x,y,z$. $\square$

Kommentti: Itse tein kilpailutilanteessa laskuvirheen vuoksi väärän valinnan $k$:lle, jonka takia todistukseni toimi muistaakseni vain kun $n\ge 600$, joka on suuri ero halutusta $n\ge 100$. Tämä oli kuitenkin vain $2$ pisteen arvoinen virhe, joten se ei juurikaan haitannut minua.

Kuten todistuksesta näkyy, niin verkkojen hyödyntäminen ei ollut suinkaan tarpeellista. Verkot kuitenkin asettivat tehtävän laajempaan kontekstiin ja tämä auttoi minua hahmottamaan tilanteen paremmin. Ylipäätään etenkin kombinatoriikan tehtäviä on monesti hyvä tarkastella eri perspektiiveistä, vaikka tämä ei olisi suoraan hyödyllistä.

Tehtävä 4

Olkoon $I$ ympyrän $\Gamma$ keskipiste, ja olkoon $ABCD$ sellainen konveksi nelikulmio, että jokainen janoista $AB$, $BC$, $CD$ ja $DA$ on tangentti ympyrälle $\Gamma$. Olkoon $\Omega$ kolmion $AIC$ ympärysympyrä. Janan $BA$ jatke pisteen $A$ yli leikkaa ympyrän $\Omega$ pisteessä $X$ ja janan $BC$ jatke pisteen $C$ yli leikkaa ympyrän $\Gamma$ pisteessä $Z$. Janojen $AD$ ja $CD$ jatkeet pisteen $D$ yli leikkaavat ympyrän $\Omega$ pisteissä $Y$ ja $T$, vastaavasti. Osoita, että

$$AD+DT+TX+XA=CD+DY+YZ+ZC$$

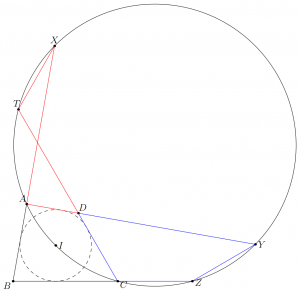
Tulee todistaa, että punaisella ja sinisellä nelikulmiolla on yhtä suuret piirit.

Lähdin liikkeelle miettimällä, miten voisin uudelleenmuotoilla todistettavan ehdon. Tehtävässä oli ainakin yksi minulle entuudestaan tuttu rakenne eli nelikulmioiden sisäympyröiden ja pituuksien summien yhteys. Tarkemmin tiesin, että Pitot’n lause kertoo, että jos nelikulmiolla $ABCD$ on sisäympyrä, niin $AB+CD=BC+DA$. Tämä lause on suhteellisen yksinkertainen, mutta siitä huolimatta se voi olla sangen vahvakin tulos oikeissa paikoissa.

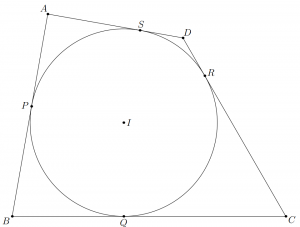
Lauseen todistus on myös jotakuinkin helppo: Olkoon $P$, $Q$, $R$ ja $S$ sivujen $AB$, $BC$, $CD$ ja $DA$ sivuamispisteet sisäympyrän kanssa, vastaavasti. Nyt $$AB+CD=(AP+PB)+(CR+RD)=(SA+BQ)+(QC+DS)=BC+DA\ \square$$

Puolen tunnin säädön jälkeen uudelleenmuotoilusta ei kuitenkaan tullut mitään. Lähdin siis tekemään sitä, millä minun olisi pitänyt aloittaakin: Piirsin monta diagrammia, lisäsin paljon pisteitä ja suoria ja tein havaintoja. Vain muutaman minuutin jälkeen huomasin, että suorat $XY$ ja $ZT$ olivat yhdensuuntaisia. Lähes heti perään tein vielä vahvemman havainnon, jonka mukaan $IXY$ ja $IZT$ ovat tasakylkisiä.

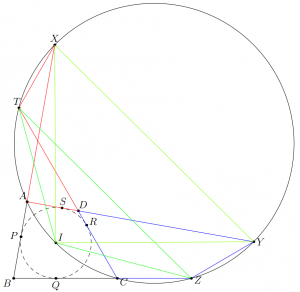
Näiden todistaminen oli pelkkää kulmanjahtaamista: Sillä $AI$ ja $CI$ ovat kulmien $\angle BAD$ ja $\angle DCA$ kulmanpuolittajat vastaavasti, diagrammin mukaisesti saadaan $$\angle IXY=\angle IAY=\angle BAI=180^{\circ}-\angle IAX=\angle XYI$$ eli $IXY$ on tasakylkinen. Kolmion $IZT$ tasakylkisyys todistuu vastaavasti.

Toisaalta aiemmassa kulmanjahtauksessa saattaa esiintyä ongelmia, jos esimerkiksi $A$ ja $Y$ ovat samalla kaarella $IX$. Näitä kutsutaan konfiguraatio-ongelmiksi, ja näitä välttääkseni käytin tavallisten kulmien sijasta suunnattuja kulmia. Näistä löytyy lisää esimerkiksi Evan Chenin kirjasta Euclidean Geometry in Mathematical Olympiads (EGMO) tai monisteesta How to Use Directed Angles (pdf).

Nyt sillä $XTZY$ on jännenelikulmio, $IXY$ ja $IZT$ tasakylkisyys tarkoittaa, että myös $XTZY$ on tasakylkinen ja siten $TX=YZ$. Siispä tämä termi eliminoituu summasta ja riittää todistaa, että $$AD+DT+XA=CD+DY+ZC$$

Tätä varten palasin Pitot-ideaan, mutta lauseen suoran hyödyntämisen sijasta imitoin sen todistusta. Tarkemmin, lisäsin pisteet $P,Q,R,S$, kuten aiemmin, ja sievensin $$AD+DT+XA=(AS+SD)+DT+XA=(AP+DR)+DT+XA=TR+XP$$ $$CD+DY+ZC=(CR+RD)+DY+ZC=(SD+CQ)+DY+ZC=SY+ZQ$$

Lopulta riitti todistaa, että $TR+XP=SY+ZQ$ Tämä oli kuitenkin selvää: Kolmiot $IPX$ ja $ZQI$ ovat suorakulmaisia yhtä pitkällä kateetilla ja hypotenuusalla, joten ne ovat yhteneviä ja siten $XP=ZQ$. Vastaavasti $XP=SY$, eli olemme valmiit. $\square$

Kommentti: Tämä tehtävä oli poikkeuksellinen siinä mielessä, että yleensä matematiikkaolympialaisten geometriatehtävät eivät käsittele hyvin laskennallisia suureita, kuten pinta-aloja ja piirejä.

Etenkin ensimmäiset ja neljännet geometriatehtävät perustuvat monesti pelkkään kulmajahtaamiseen. Siinä mielessä tämä tehtävä vaati myös jonkin verran geometrista intuitiota. Minulle ainakin oli iso hyöty tietää etukäteen, että aina kun nelikulmiolla on sisäympyrä, sen sivujen pituuksien summat ovat tärkeitä.

---

Tilaa Dimension uutiskirje – saat sähköpostiisi aina kuunvaihteessa koosteen tuoreimmista artikkeleista