Kombinatoriikkaa laskimella
Laskimella tehdään lukioissa nykyään sitä, mihin se ei sovi. Sitä käytetään kirjoituskoneena ja sillä piirretään vaivalloisesti hahmotelmakuvia sekä merkkikaavioita. Sen sijaan sillä ei tehdä sitä, mihin se sopii. Ei hyödynnetä tekniikoita, jotka toimivat laskimella, mutta eivät kynällä ja paperilla. Tässä kirjoituksessa esittelen yhden lähestymistavan kombinatoriikkaan. Tapa on kätevä laskimella, mutta ei ilman sitä. Asia menee vähän yli lukiokurssin – ei kuitenkaan paljon.
Kahden nopan heitto
Tarkoituksena on ratkaista tietynlaisia kombinatorisia ongelmia algebrallisesti. Käytän johdatteluun George Pólyan esittämää kuvakirjoitusmenetelmää ja laskimena TInspireä. Muut cas-laskimet toimivat samalla tavalla.
Heitetään kahta noppaa, keltaista ja vihreää. Mahdolliset yhdistelmät voidaan esittää kuvana, kun ajatellaan, että JA-sanaa vastaa kertolasku ja TAI-sanaa summa:
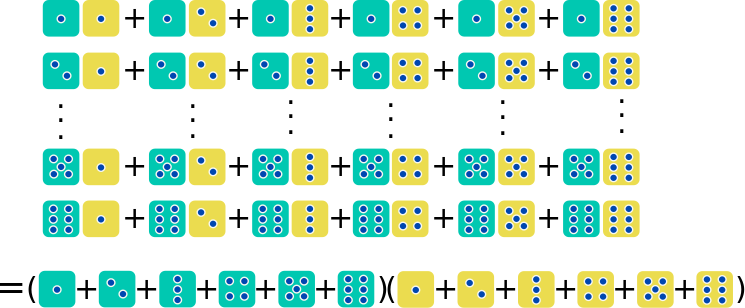
Halutaan selvittää noppien silmälukujen summan jakauma. Silloin saadaan seuraava tuttu kaavio:
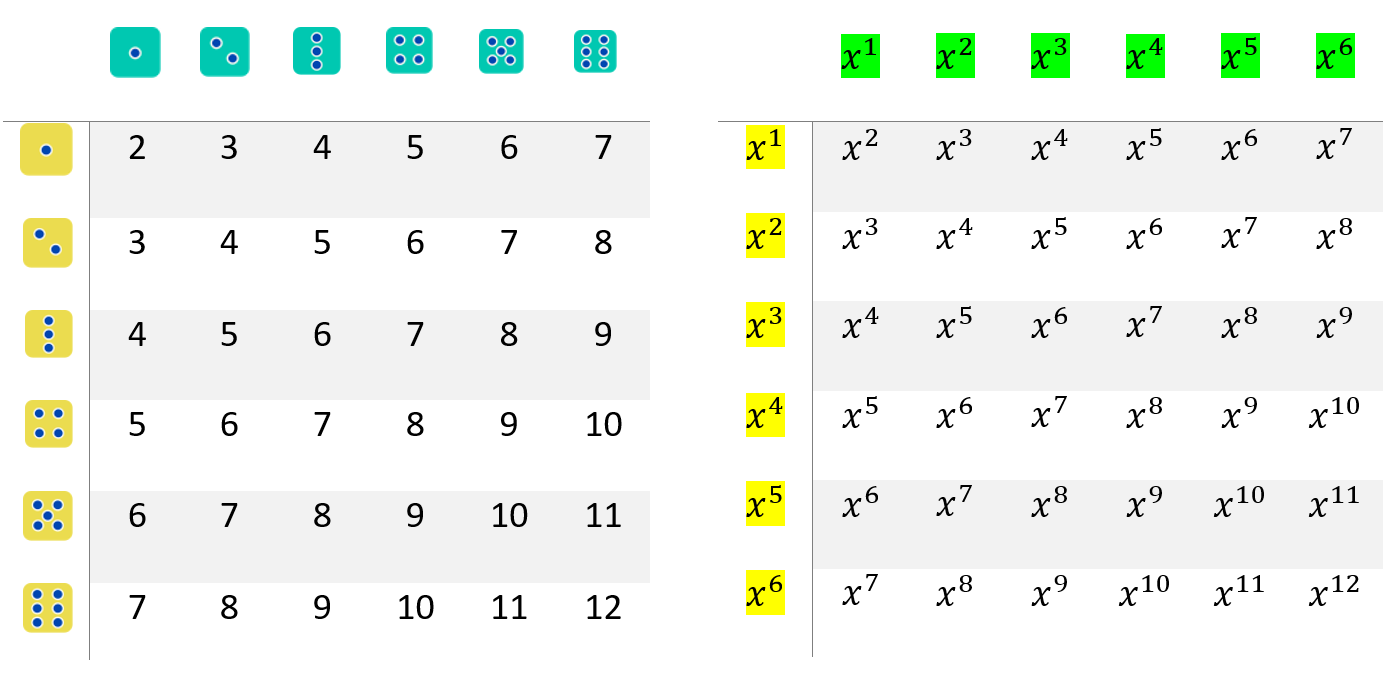
Jos kirjoitetaan näkyviin $x$:n potenssien kertotaulu, huomataan, että tulojen potenssit ovat täsmälleen samat kuin ensimmäisen taulukon silmälukujen summat. Tämä antaa aiheen merkitä

Silloin eri noppien silmälukujen yhdistelmät saadaan tulona

=$(x+x^2+x^3+x^4+x^5+x^6)(x+x^2+x^3+x^4+x^5+x^6)$
=$(x+x^2+x^3+x^4+x^5+x^6)^2$
Tämän auki laskeminen on helppoa laskimella
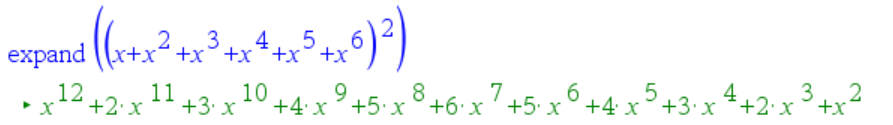
Saatuun polynomiin on laskettu yhteen kaikki samat $x$:n potenssit. Siis esimerkiksi potenssin $x^5$ kertoimesta voidaan lukea, että noppayhdistelmiä, joissa silmälukujen summa on 5, on neljä kappaletta, koska polynomissa on termi $4x^5$. Vastaavasti termistä $5x^8$ nähdään, että yhdistelmiä, joissa silmäsummaksi tulee 8, on viisi kappaletta.
Useamman nopan tapaus
Selvitetään seuraavaksi silmälukujen summan jakauma kolmen nopan heitossa. Se saadaan seuraavan polynomin kertoimista:
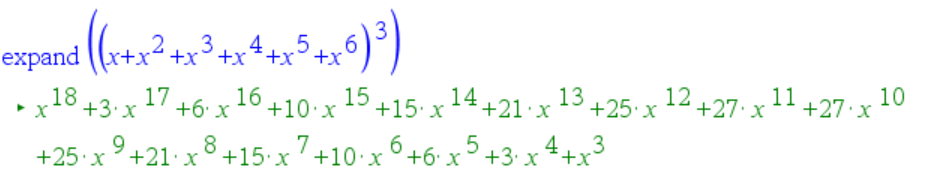
Jos halutaan saada kunkin silmäsumman todennäköisyys, riittää painottaa jokainen noppalukema omalla todennäköisyydellään:
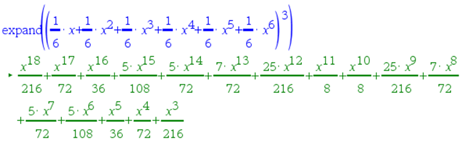
Siis kolmen nopan heitossa todennäköisyys saada silmäsummaksi esimerkiksi 8 on $\frac{7}{72}$.
Tämä ajatus yleistyy helposti. Jos heitetään kuuttakymmentä noppaa ja lasketaan silmäluvut yhteen, tapahtumaa vastaa polynomi $(x+x^2+x^3+x^4+x^5+x^6\ )^{60}$. Laskin ehkä aukaisee nämä sulut expandilla, mutta polynomi on kammottavan pitkä. Jos kuitenkin halutaan tietää ainoastaan, kuinka monella tavalla voidaan saada silmälukujen summaksi vaikka 120, riittää saada selville vain potenssin $x^{120}$ kerroin $a_{120}$. Mutta miten löydetään laskimella polynomin tietynasteisen termin kerroin laskematta auki koko polynomia? Ratkaisu perustuu siihen, että potenssin $x^k$ $n$:nnäs derivaatta kohdassa $x=0$ on
$\left[\frac{d^n}{dx^n}x^k\right]_{x=0}=0$, jos $n\ne k$, mutta
$\left[\frac{d^k}{dx^k}x^k\right]_{x=0}=k!$
Pienellä päättelyllä huomataan siis, että kerroin $a_{120}$ saadaan polynomista $(x+x^2+x^3+x^4+x^5+x^6\ )^{60}$ ottamalla
$\frac{1}{120!}\left[\frac{d^{120}}{dx^{120}}\left(x+x^2+x^3+x^4+x^5+x^6\right)^{60}\right]_{x=0}$
Yllättäen laskin jaksaa laskea näinkin rankan derivaatan (kohdassa 0).
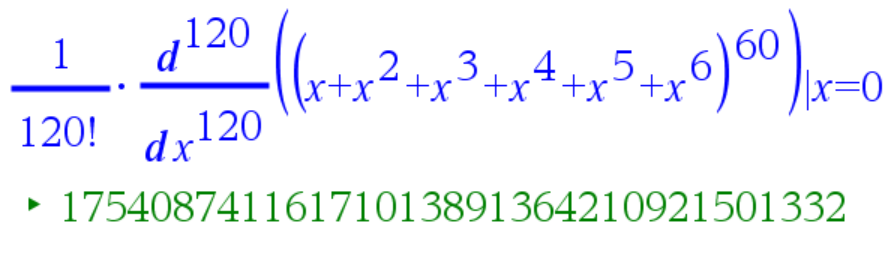
Eli heitettäessä kuuttakymmentä noppaa on 17540874116171013891364210921501332 tapaa saada silmälukujen summaksi 120.
Kuinka rikkoa kaksikymppinen?
Seuraava esimerkki on peräisin suoraan Pólyalta. Kuinka monella tavalla voidaan rikkoa 20 euroa käyttäen 10 ja 5 euron seteleitä sekä 2 ja 1 euron kolikoita? Siis esimerkiksi 20 = 5 + 5 + 10 ja 20 = 1 + 2 + 2 + 5 + 10. Tässä järjestyksellä ei ole väliä, joten 5 + 5 + 10 = 10 + 5 + 5 jne.
Euron kolikoita voi olla summassa 0, 1, 2, 3, … , 20 kappaletta. Jos kertolasku on JA ja yhteenlasku on TAI, saadaan yhden euron kolikoiden mahdollisille lukumäärille kuvallinen esitys:
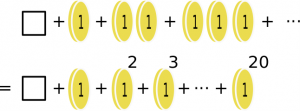
Tässä neliö tarkoittaa, että yhtään yhden euron kolikkoa ei käytetä (eli käytetään 0). Jos merkitään
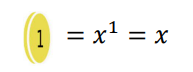
ja lisäksi asetetaan neliön paikalle $x^0=1$ , voidaan edellä oleva summa kirjoittaa
$1+x+x^2+x^3+\ldots+x^{20}$.
Kahden euron kolikoita voi olla summassa 0, 1, 2, 3, … , 10 kappaletta. Kahden euron kolikoiden lukumäärä voidaan valita summasta
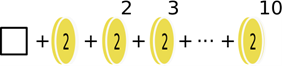
Jos asetetaan
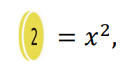
voidaan ylläoleva polynomi kirjoittaa $1+x^2+x^4+x^6+\ldots+x^{20}$ .
Viiden euron seteleitä voi olla summassa 0, 1, 2, 3, 4 kappaletta, joten saadaan kuten edellä polynomi $1+x^5+x^{10}+x^{15}+x^{20}$. Lopulta kymmenen euron seteleiden valintaa kuvaa polynomi $1+x^{10}+x^{20}$.
Rikottaessa kahtakymppiä pitää siis valita jokaisesta edellisestä polynomista yksi termi, joka voi olla myös 1, jos kyseistä rahatyyppiä ei käytetä ollenkaan. Kun nämä valinnat kerrotaan, termien potenssit lasketaan yhteen ja tämän summan on oltava 20. Siis halutaan tietää potenssin $x^{20}$ kerroin tulossa
$(1+x+\ldots+x^{20})(1+x^2+\ldots+x^{20})(1+x^5+\ldots+x^{20})(1+x^{10}+x^{20})$.
Se saadaan helposti laskimella:
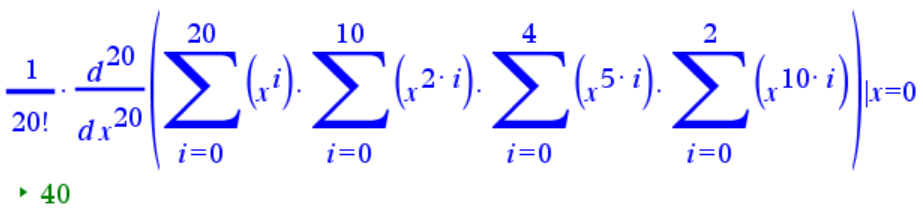
Tapoja on siis 40.
Reittien lukumäärä
Tarkastellaan vielä seuraavaa kysymystä: Kuinka monta eri reittiä on kuvan ruudukossa origosta pisteeseen (1, 5), jos liikkumiseen käytetään tasan kaksitoista askelta? Askeleet voivat olla oikealle, vasemmalle, ylös tai alas, ja edestakaisin liikkuminen sallitaan.
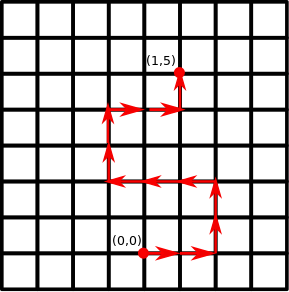
On ilmeistä, että valinnat muodostavat symbolisen lausekkeen
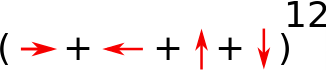
Tuntuu luonnolliselta kirjoittaa tämä muotoon
$(x+x^{-1}+y+y^{-1}\ )^{12}$,
missä $x$ on siirtymä $x$-akselin suunnassa ja $y$ siirtymä $y$-akselin suunnassa. Etsitään tässä lausekkeessa, joka tällä kertaa ei ole polynomi, potenssin $x^1y^5$ kerroin. Se onnistuu joko expandilla, tai selvittämällä polynomin
$x^{12}\ y^{12}\ (x+x^{-1}+y+y^{-1}\ )^{12}$
potenssin $x^{13}y^{17}$ kerroin.
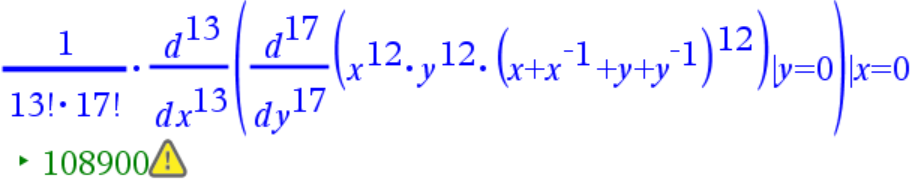
Reittejä on siis 108900.
Lopuksi
Laskimen käyttö matematiikassa vaikuttaa pitkällä aikavälillä paitsi siihen, miten matematiikkaa kirjoitetaan, myös siihen, minkälaiset ratkaisumenetelmät hyväksytään. Edellä esitetyt tekniikat vaativat vahvan laskimen, joka kykenee nopeasti avaamaan sulut ja derivoimaan monta kertaa peräkkäin. Näillä menetelmillä ei saada ratkaisuja valmiina lausekkeina. Sulkakynällä laskevan matemaatikon kannalta tällainen lähestymistapa on hyödytön tai ainakin epäkäytännöllinen. Vastaavasti laskimen käyttäjälle käsinkirjoitustekniikat, jotka ovat vaikuttaneet esimerkiksi matematiikan merkintätapoihin, ovat vaivalloisia.
Laskimen tuominen osaksi matematiikkaa ja sen opetusta ei siis ehkä ole vailla syvällisiäkään seurauksia. Matematiikassa tekniikka on sisältöä. ”Väline on viesti”, niin kuin Marshall McLuhan sanoi.
Lähteet
George Pólya: On Picture-Writing, The American Mathematical Monthly, 1956, vol. 63, issue 10.







