Laatoitusten geometriaa

Katukiveykseen tai seinälaatoitukseen liittyy säännöllisen toistumisen mielikuva. Matemaattisesti kyse on kuvioiden symmetriaominaisuuksista. Vain mielikuvitus on rajana, sillä säännöllisen ja säännöttömän raja ei ole jyrkkä.

Arkkitehtuurissa friisi (engl. frieze) tarkoittaa rakennuksen julkisivussa olevaa kohokuvioin koristeltua aluetta tai sisäseinässä olevaa pitkänomaista koristemaalausta. Matemaattisesti friisi on yhteen suuntaan siirtosymmetrinen kuvio, joka voi olla myös peilaus- tai kiertosymmetrinen. Friiseillä on seitsemän symmetriaryhmää. Luokittamiseen käytetään useita erilaisia merkintätapoja [1].

Monista monikulmioista, useimmin neliöistä tai suorakulmioista, saadaan tavanomaisen katukiveyksen kaltaisia laatoituksia, joita voidaan ajatella jatkettavan tason peittoina rajatta kaikkiin suuntiin. Ne ovat useimmiten kierto-, peilaus- tai siirtosymmetrisiä. Viimeksi mainittuja kutsutaan myös jaksollisiksi (engl. periodic), koska sama kuvio toistuu aina määrämatkan jälkeen. Tällaisia tason peittoja ovat myös monet M. C. Escherin maalaukset, vaikka peruslaattojen rajoja ei ole kuviin piirrettykään.

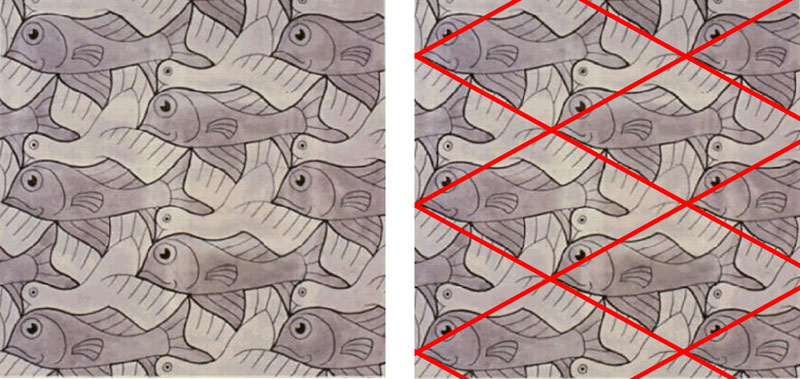
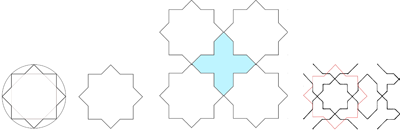
Matemaattisesti laatoitus (engl. tiling) on tapa peittää taso siten, että kuvioiden väliin ei jää rakoja tai reikiä. Laatoitukset voidaan luokitella symmetriaominaisuuksiensa perusteella. Luokkia, tason symmetriaryhmiä eli seinäpaperiryhmiä [2], on 17. Todistus, että niitä on tasan 17, on runsaan sadan vuoden ikäinen. Se ei ole kuitenkaan ihan helppo, sillä se keksittiin vasta sen jälkeen, kun kolmiulotteisen avaruuden symmetriaryhmät oli selvitetty. Kaikki symmetriaryhmät olivat käytössä jo esimerkiksi arabialaisten rakentajien töissä, yksin Alhambran linnan kuvioissa Espanjan Granadassa esiintyy 13 näistä 17 symmetriaryhmästä.

Penrosen laatoiksi (engl. Penrose tiles) sanotaan kahta lävistäjänsä suhteen peilisymmetristä nelikulmiota, joiden vastakkaiset sisäkulmat ovat kuperassa nelikulmiossa 72 ja 144 astetta sekä koverassa 72 ja 216 astetta [5]. Näistä voidaan koota useita erilaisia laatoituksia, jotka voivat olla peili- tai siirtosymmetrisiä. Myös viisinkertainen kiertosymmetria on mahdollinen. Jaksollisuus voidaan estää kieltämällä tietyt vierekkäisten laattojen asennot. Tämä voidaan tehdä lisäämällä laattojen reunoihin koloja ja niitä vastaavia ulokkeita tai piirtämällä laattoihin kaaret, joiden pitää muodostaa laattojen reunojen yli jatkuvia viivoja. Tarkasti ottaen Penrosen laattoja on kolmenlaisia, mutta edellä mainittu pari on ylivoimaisesti tunnetuin.

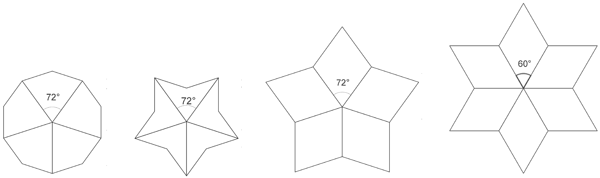
Rissasen laatoituksia [6] voidaan pitää Penrosen laatoituksen yleistyksenä. Niiden peruskuviot ovat neljäkkäitä, joiden vierekkäiset kulmat suhtautuvat kuin luonnolliset luvut. Niistä voidaan koota monenlaisia laatoituksia, myös jaksollisia. Erityisen mielenkiintoisia ovat ne, joissa kulmien suhde on 2 : (n − 2), missä n on kahta suurempi luonnollinen luku. Suhdelukua 2 vastaavan kulman suuruus on , joten n tällaista peruskuviota voidaan asettaa yhteisen kärkipisteen ympärille. Näistä muodostuu ruusua muistuttava kuvio. Siitä lähtevä laatoitus on kiertosymmetrinen ja jaksoton. Peruskuvion mukaan siitä käytetään nimeä sub rosa [7]. Laatoitusjärjestelmän keksi suomalainen kuvataiteilija Markus Rissanen vajaat kymmenen vuotta sitten.

Jaksottomilla Penrosen ja Rissasen laatoituksilla on sama mielenkiintoinen ominaisuus. Ne eivät ole siirtosymmetrisiä, mutta kuitenkin valejaksollisia (engl. quasiperiodic). Tämä tarkoittaa sitä, että jokainen laatoituksessa esiintyvä äärellinen kuvio, olipa se kooltaan kuinka suuri hyvänsä, voi esiintyä muuallakin samassa laatoituksessa äärettömän monta kertaa. Esiintyminen ei ole säännöllistä ja laatoituksessa voi olla yhä suurempia alueita ilman kyseistä kuviota. Matemaattisesti tämä voidaan muotoilla niin, että jokaiselle kuviolle K on olemassa sellainen etäisyys R, että kuvio K on enintään etäisyydellä R mittauskohdasta, mitattiinpa mistä laatoituksen kohdasta tahansa. Etäisyys R(K) luonnehtii siis kuvion K esiintymistiheyttä. Esimerkiksi ruusuja esiintyy siis kaikkialla sub rosa -laatoituksessa.

Suuret kiitokset tästä jutusta ansaitsee Turun yliopiston matematiikan professori Jarkko Kari, jonka esittämästä huomautuksesta juttuidea syntyi ja joka on auttanut jutun yksityiskohtien tarkentamisessa.

Lisää luettavaa

[1] Frieze group. Wikipedia-artikkeli https://en.wikipedia.org/wiki/Frieze_group, viitattu 1.9.2018.

[2] Wall paper group. Wikipedia-artikkeli https://en.wikipedia.org/wiki/Wallpaper_group, viitattu 1.9.2018.

[3] Rønning, Fr. Islamic petterns and symmetry groups. Osoitteessa https://fi.wikipedia.org/wiki/Penrosen_laatat, viitattu 1.9.2018.

[6] Kari, J. ja Rissanen, M. Sub Rosa, a system of quasiperiodic rhombic substitution tilings with n-fold rotational symmetry. Cornell University Library, arXiv.org 2015, https://arxiv.org/abs/1512.01402, viitattu 15.8.2018. Ilmestynyt 2017 Discrete & Computational Geometry -lehdessä.

[7] Korhonen, H. Sub rosa. Dimensio 6/2018 s. 40–41.