Matriisimekaniikkaa yleistajuisesti. Osa 2.
Johdanto
Artikkelissani ”Kolmoispolarisaattoriparadoksista yleistajuisesti” (Dimensio 16.11.2021) esittelin (fotonien) epälokaalin todellisuuden kuvailuun sopivia matemaattisia työkaluja. Paradoksi lakkaa olemasta paradoksi vasta, kun sen mikroskooppisessa tarkastelussa otetaan käyttöön matriisit. Kvanttimekaniikan perustamisjulkaisujen satavuotisjuhlapäivän lähestyessä [1] tavoitteenani on tuoda yleistajuisesti esiin kaksi saavutusta, jotka teoreettisessa fysiikassa on tehty kuluneena vuosisatana matriisimekaniikan avulla ja ansiosta. Edellisen artikkelini jatko-osaksi tarkoittamassani kirjoituksessa etenen kaksitilasysteemistä kaksihiukkassysteemiin, jonka esimerkkinä esitän ydinspinien kytkeytymisen vetymolekyylissä (esimerkki on analoginen elektronien spinien kytkeytymiselle He-atomissa).
Toisena esimerkkinä esitän kaksitilasysteemin laajennuksena neutraalin kaonin (ts. oudon mesonin) oskillaation ja hajoamiset, joissa 1964 havaittiin CP-symmetriarikko. Neutraali kaoni oskilloi ja hajoaa, koska kvanttiluku outous ei säily heikoissa vuorovaikutuksissa. Laajempana tavoitteenani on osallistua toisen asteen pakollisten ja valinnaisten mafyke-toteutusten suunnitteluun ja keskusteluun niistä, jotta a) niihin sisältyviä matemaattisia työkaluja päivitettäisiin 21. vuosisadalle ja b) niillä olisi parempi käytettävyys sekä työelämässä että todellisuuden monimutkaisuuden ymmärtämisessä (yleissivistävä funktio).
Miksi matriisit?
Kirjassaan Helgoland Carlo Rovelli kirjoittaa oman (tutkimustyönsä tuloksena syntyneen) versionsa kvanttimekaniikan matriisimekaniikan varhaishistoriasta [2]. Kirjan nimenä on Saksalle kuuluva Pohjanmeren saari, jossa nuori Heisenberg lomaili kesällä 1925 työstäen tutkimusideoitaan. Rovelli nimeää Heisenbergin keskeisen oivalluksen “relationaalisuudeksi”, jossa hiukkaset ovat oikeastaan haamumaisia, mutta “manifestoituvat” vuorovaikutuksissa. Hän mainitsee observaabelit, joilla Heisenberg tarkoittaa hiukkasen havaittavia, mitattavia suureita, esimerkiksi paikkaa ja nopeutta. Rovelli mainitsee matriisit matemaattisina työkaluina, joilla voidaan lähestyä mikroskooppisia prosesseja kvantitatiivisesti ilman, että kaikki yksityiskohdat ovat tarkasti tiedossa. Systeemin kokonaisaaltofunktiosta ei tarvitse tietää kaikkea – riittää kun siitä tiedetään jotakin. Ominaisarvoyhtälössä
$$\left.\left.H\left|\mathrm{\Psi}\right.\right\rangle=E\left.\left|\mathrm{\Psi}\right.\right\rangle\right. \qquad \qquad \qquad \qquad \qquad (1)$$
esiintyvä $\left.\left|\mathrm{\Psi}\right.\right\rangle$ = psii on aaltofunktio, joka pyritään matemaattisesti saamaan ortogonaalisten kompleksisten kantavektorien joukon muotoon (parhaimmillaan tai yksinkertaisimmillaan psii voidaan esittää kahden ortogonaalisen kantavektorin lineaarikombinaationa ts. superpositiona). Kaksitilasysteemin potentiaali- ja liike-energioihin liittyvää a priori -tietoa (etukäteistietoa) viedään Hamiltonin operaattoriin $H$, joka on 2×2 matriisi. Yhtälön ominaisarvoina saadaan energiat, jotka ovat skalaareja. Matriisien ominaisuuksia voidaan tutkia esimerkiksi Wolfram Alphalla, jonka ilmaisversion ”lineaarialgebra” -moduulissa voidaan laskettaa mielivaltaisen 2×2 matriisin ominaisarvot ja ominaisfunktiot. Tällainen alkeellisin formalismi on toimiva esimerkiksi ”kvanttibitin” eli kubitin kuvauksena. Kubitilla on lukuisia fysikaalisia realisaatioita, mm. vedynkaltaisen atomin kaksitilasysteemi tai tasopolarisoidun fotonin kaksitilasysteemi. Muista sovelluksista mainittakoon maser ja sen sovelluksena atomikello. Kytketyillä kubiteilla toteutettavien ”kvanttiporttien” malleissa käytettävät matriisit ovat tyypillisesti 4×4 matriiseja.
Matriisimekaniikan fysikaaliseen esitykseen kuuluu operaattoriformalismi, jonka avulla Heisenbergin epätarkkuusperiaatteen taustalla oleva ”kanoninen kvantisointi” saa muodon
$$XP-PX=iħ \qquad \qquad \qquad \qquad \qquad (2)$$
$XP-PX=\left[X,P\right]$ on paikka- ja liikemääräoperaattorien kommutaattori ja on siis $≠ 0$. Yhtälö tarkoittaa sitä, että mainitut operaattorit eivät kommutoi vaan niiden kommutaattori on iħ, jossa ħ on ”redusoitu Planckin vakio” eli Diracin vakio $\frac{h}{2\pi}$. Tässä lienee paikallaan muistuttaa, että Planckin vakion yksikkö on Js, ja että näin ollen ei-kommutoiva suurepari on myös energia ja aika. Samoin sähköenergian ja ajan tulosta muodostettava sähkövaraus (yksikkö As) ja ”magneettivaraus” (yksikkö Vs), joiden mikroskooppisena suhteena ”kvanttiohmiksi” eli von Klitzingin vakioksi saadaan $\frac{h}{e^2}$ (eli Planckin vakio jaettuna alkeisvarauksen neliöllä).
Carlo Rovelli esittää kirjassaan [2] yhtälön (2) ja olettaa, että lukija tunnistaa operaattoriformalismiin sisältyvän ”matriisimekaniikan” ts. sen, että tavallisten lukujen kyseessä ollen lukujen $X$ ja $P$ kommutaattori olisi nolla (kertolaskun vaihdantalaki). Matriisitulo $XP$ sitä vastoin voi olla erisuuri kuin $PX$. Yhtälöstä (2) edetään epätarkkuusperiaatteeseen tarkastelemalla ei-kommutoivien suureiden odotusarvoja* ja laskemalla suureille keskihajonnat
$\sigma_X=\sqrt{\langle X\rangle^{2}-\langle X\rangle^{2}}$ ja
$\sigma_X=\sqrt{\langle P\rangle^{2}-\langle P\rangle^{2}}$, joista muutamalla stepillä saadaan tulos
$\sigma_X\sigma_P\ge \frac{ħ}{2} \qquad \qquad \qquad \qquad \qquad (3)$
*Observaabelin $O$ odotusarvo $\langle O \rangle$ voidaan laskea tiheysmatriisista $\rho$ käyttäen kaavaa
$\langle O\rangle =Tr[\rho O]=\sum _{ij}w_{ij}O_{ji}$, jossa $Tr$ on matriisin jälki ja $O_{ji}$ on operaattorin $O$ matriisielementti.
Tiheysmatriisi $\rho=\sum_{ij} w_{ij}\left|\left.i\right\rangle\left\langle j\right.\right|$ jossa $w_{ij}$ ovat kompleksikertoimia ja $\left.|i\right\rangle$ ominaistiloja (tai tilavektoreita). Oletetaan, että tilat $\left\{\left.|i\right\rangle\right\}$ muodostavat täydellisen kannan. Merkitään, että näitä vastaavien konjugaattitilojen joukko on $\left\{\left\langle j\right.|\right\}$.
Matriisielementti on kvanttimekaniikassa käytetty termi, jonka avulla observaabelia kuvaavalle lineaarioperaattorille saadaan aikaiseksi matriisiesitys. Matriisielementti $O_{ji}$ lasketaan operaattorista $O$ operoimalla siihen vasemmalta ja oikealta tilavektoreilla.
$$O_{ji}=\left\langle j\middle| O\middle| i\right\rangle$$
Kaksitilasysteemistä kaksihiukkassysteemiin
Edellä mainitun kaksitilasysteemin täydellinen kuvaus vaatisi Paulin spinorien eli spinmatriisien tarkastelun. Tavoitteenani on kuitenkin mennä eteenpäin, ts. siirtyä kaksitilasysteemistä kaksihiukkassysteemiin. Tämän tarkastelun jälkeen voidaan vielä konkreettisemmin vastata kysymykseen Miksi matriisit?
Historiallisesti, Werner Heisenbergin vuonna 1932 saaman fysiikan Nobelin palkinnon perusteluissa mainitaan erikseen hänen kontribuutionsa vedyn spinisomerian selitykseen, jonka hän teki Friedrich Hundin kanssa 1927. Selitystä edelsi Wolfgang Paulin 1924-25 lanseeraama fermionin (aluksi elektronin) uusi kvanttiluku (myöhemmin ”spin”), joka saa arvot -½ ja +½. Hiukkaset jaetaan fermioneihin ja bosoneihin sen mukaan, onko niiden spin puolilukuinen vai kokonaislukuinen. Paitsi elektroni myös ytimen protoni (ja neutroni) ovat fermioneja, jolloin monet atomiytimet ovat yhdistelmäbosoneja. Spinejä voidaan siis laskea yhteen. Katsotaan hieman tarkemmin, miten tuo yhteenlasku tapahtuu. Unohdetaan hetkeksi elektronit ja tarkastellaan alkeellisinta molekyyliä, kaksiatomista vetymolekyyliä. Siinä kaksi vety-ydintä eli protonia kytkeytyy toisiinsa siksi, että ne tulevat lähelle toisiaan. Monet molekyylien ominaisuudet selittyvät elektroniverhojen (molekyyliorbitaalien) ominaisuuksilla, mutta tässä vetykaasun tapauksessa havaitaan alhaisessa lämpötilassa anomaalisia faasimuutoksia ja varioivia termodynaamisia suureita kuten ominaislämpökapasiteetteja, joiden selitys on ydinfysikaalinen/kvanttimekaaninen.
Klassisen todennäköisyyden kontekstissa, jos heitetään kahta kolikkoa, saadaan neljä erilaista alkeistapausta, koska kumpikin binäärisen kolikon heitto on riippumaton tapahtuma. Vety-ydinten (binääristen) spinien kytkeytyminen poikkeaa kolikonheitosta siten, että spinit eivät kiepu vapaasti ilmassa tai tyhjiössä vaan niillä on molekyylirotaationa tunnettu rataliike kontekstinaan. Samaan tapaan atomin elektronien spinien kytkeytymisellä vaikkapa He-atomissa on kontekstinaan atomiorbitaali, s-kuori. Paulin kieltosääntö tarkoittaa tätä kontekstisidonnaisuutta. Jos kahden elektronin kontekstina on pallosymmetrinen s-orbitaali, niiden spinien on oltava vastakkaiset ja vieläpä niin, että ne eivät voi vaihtua toisikseen. Kaikki kvanttiluvut kummallakin eivät voi olla samoja; fermionien kokonaisaaltofunktio on antisymmetrinen. Matriisimekaniikan kannalta oleellinen steppi tässä on se, että a priori -tietoa ei viedä ainoastaan ”hamiltoniin” vaan myös aaltofunktioon, joka separoidaan ydinosaan ja elektroniseen osaan ja jonka elektroninen aaltofunktio separoidaan edelleen rata- ja spinosiin. Bornin – Oppenheimerin approksimaatio olettaa elektronisen siirtymän niin nopeaksi, että se tapahtuu vakiona pysyvässä ydinkonfiguraatiossa. Ydinkonfiguraatioiden hitailla muutoksilla ei yleensä ole vaikutusta kemiassa, mutta poikkeuksiakin tästä säännöstä on; vedyn spinisomerian lisäksi muun muassa kineettinen isotooppiefekti (KIE) D2O:n teollisessa valmistuksessa.
Edellä esittämäni perusteella on siis yhdentekevää, kirjoitetaanko aaltofunktion spinosa kahdelle elektronille vai kahdelle protonille (mikäli niiden kontekstit ovat riittävän samanlaiset). Oleellista on, että spinosa voi olla spinien vaihdon suhteen symmetrinen tai antisymmetrinen, jolloin rataosan on oltava vastaavasti antisymmetrinen tai symmetrinen, tässä järjestyksessä, jotta kahden fermionin kokonaisaaltofunktio on antisymmetrinen. Jos kolikonheitossa mahdollisia tuloksia saadaan neljä, niin atomi- ja molekyylispektroskopiassa havaitaan singlettitiloja ja triplettitiloja. Triplettitilaa vastaavassa aaltofunktion spinosassa käytetään kaikki neljä (spinien vaihdon suhteen symmetristä) ”kolikonheittoa” seuraavasti:
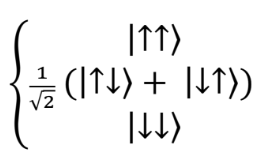
jolloin singlettitilaa vastaava aaltofunktion spinosa on spinien vaihdon suhteen antisymmetrinen $\frac{1}{\sqrt2}\left.\ (\left|\uparrow\downarrow\right.\right\rangle-\left. \ \left|\downarrow\uparrow\right.\right\rangle). \qquad \qquad \qquad \qquad \qquad (4)$
Tässä vähennyslaskun antikommutatiivisuus tuottaa halutun lopputuloksen: spinosassa merkki vaihtuu, jos spinit ”flippaavat” ts. vaihtuvat toisikseen. Kun tätä tulosta verrataan yhtälöön (2) huomataan (matriisimekaniikan kontekstissa), että atomin tai molekyylin perustilalla voi olla nollasta poikkeava energia. Matriisimekaniikka onnistuu havaittavan todellisuuden kuvauksessaan ja ennustaa lisäksi nk. nollapiste-energian atomeilla, molekyyleillä, bosonisilla ja fermionisilla kondensaateilla jne. Ortovedyn (triplettivedyn) tapauksessa molekyylin kokonaisydinspin I = 1, jolloin tietyn akselin suhteen katsottu komponentti MI saa arvot +1, 0 tai -1 siinä missä paravedyn (singlettivedyn) kohdalla I = 0 ja MI = 0.
CP-symmetria neutraalin kaonin hajoamisissa
Matriisimekaniikan saavutusten lista on pitkä. Listalla olisi esimerkiksi CKM-matriisi, joka ennustaa sen, että kvarkkiperheitä on kolme. Se ennustaa lisäksi heikossa vuorovaikutuksessa havaittavat symmetriarikot. Listalla voisivat olla Paulin matriiseista yleistetyt Gell-Mannin matriisit, joita käytetään vahvan vuorovaikutuksen kuvauksessa ja jotka ennustavat gluonien dispersion. Yleistajuiseen artikkeliini valitsin tapaustutkimukseksi matriisimekaniikkaa, jolla kuvataan heikon vuorovaikutuksen CP-symmetriaa (hiukkas–antihiukkassymmetriaa). Tapaus on lukiolaiselle relevantti, koska sen tunnetut (toisin kuin vähemmän tunnetut mutta Nobel-palkitut) tulokset löytyvät MAOLin taulukkokirjasta taulukosta ”Tavallisimmat alkeishiukkaset/Hadronit/Mesonit”.
Maailma olisi hiukan tylsä paikka, jos kaikki aine olisi baryonista, ts. muodostuisi vain protoneista ja neutroneista eli nukleoneista. Baryonit ovat kolmen kvarkin (fermionin) yhdistelmähiukkasia ja ovat itsekin fermioneja (edellä todettiin, että spinejä voidaan laskea yhteen). Atomiytimet voivat olla fermioneja tai bosoneja sen mukaan onko niissä pariton vai parillinen määrä nukleoneja. Atomiytimet ovat (luonnossa) enimmäkseen stabiileja tai hajoavat hitaasti mm. beetahiukkasia (elektroneja) ja alfahiukkasia (He-ytimiä) säteilevissä hajoamisissa. Nukleonisynteesi on osoittautunut haastavaksi tutkimuskohteeksi nukleonien suuren stabiilisuuden takia. Kosmisessa säteilyssä havaitaan kuitenkin nukleonien ja muiden baryonien lisäksi mesoneja, jotka ovat kvarkin ja antikvarkin muodostamia pareja (yhdistelmäbosoneja). Niitä tutkimalla on jo yli puoli vuosisataa saatu tietoa mm. eri kvarkkiperheiden ominaisuuksista ja vaikutuksista hadroneissa (yhteisnimitys baryoneille ja mesoneille).
Mesonin teoretisoi ensimmäisenä Hideki Yukava vuonna 1935 ja vahvan vuorovaikutuksen ensimmäinen teoreettinen malli oli nk. mesoninvaihtomalli. Heikon vuorovaikutuksen symmetria-arvoitusten historia alkaa 1950-luvulla siitä, kun ensiksi havaitaan pariteettisymmetrian rikkoutuvan kaikissa beetahajoamisissa. Pariteetti tarkoittaa likimain samaa kuin ”kätisyys”, jolloin yhden paikkakoordinaatin merkkimuunnos muuttaa hiukkasen (spinin ruuviviivan) peilikuvakseen. Pariteetti säilyy sähkömagneettisessa ja vahvassa vuorovaikutuksessa ja gravitaatiossa. On kuitenkin osoittautunut, että heikossa vuorovaikutuksessa se ei säily. Hiukkasfysiikan standardimalliin liittyy pariteetin rikkoutuminen. Sen mukaan heikkoon vuorovaikutukseen osallistuu vain tavallisten hiukkasten vasenkätinen komponentti ja antihiukkasten oikeakätinen komponentti. Tämä osoittaa, että pariteetti ei ole maailmankaikkeuden universaalinen symmetriaominaisuus.
Pariteetti on toisaalta sama asia kuin ”parillisuus”, se on multiplikatiivinen kvanttiluku ja voidaan suoraan sanoa, että jos yksi ja sama hiukkanen hajoaa toisaalla kahdeksi hiukkaseksi ja toisaalla kolmeksi hiukkaseksi, tapahtumiin täytyy liittyä ”pariteettirikko”. Tämä on tilanne juuri silloin, kun positiivisesti varattu kaoni hajoaa kahdeksi tai kolmeksi kevyemmäksi mesoniksi (pioniksi). ”Tau – theeta -arvoitus” (”τ – θ puzzle”) ei ole vielä löytänyt tietään MAOLin taulukkokirjaan, jossa K+:n ilmoitetaan hajoavan (hadronisesti) kahdeksi pioniksi tai (leptonisesti) antimyoniksi ja myonin neutriinoksi.
Jotta tässä yleistajuisessa esityksessä päästään eteenpäin, kerron seuraavaksi että ”pariteettirikon” synnyttämä hämmennys korjattiin pian ilmoittamalla, että varaus – pariteetti- eli CP-symmetria on todellinen hiukkas–antihiukkassymmetria ja säilyy. CP on multiplikatiivinen kvanttiluku, jonka oletettiin säilyvän heikon vuorovaikutuksen hajoamisissa. Toisin sanoen, jos P ei säily, myöskään C ei säily, jolloin CP säilyy.
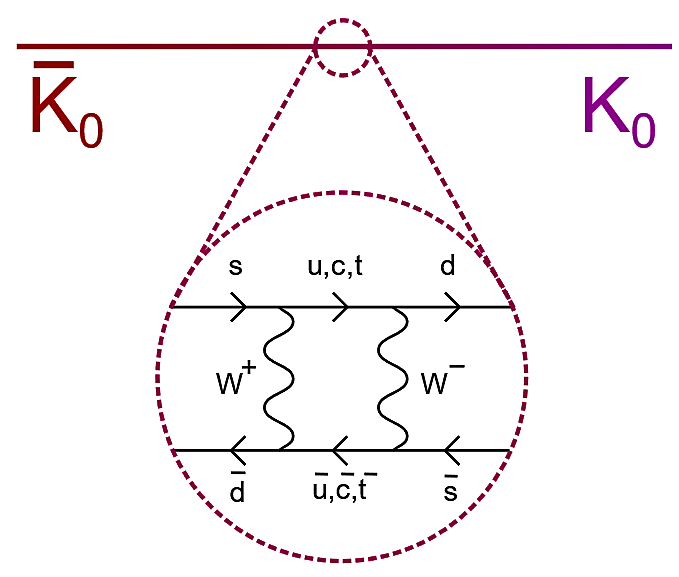
Nyt päästään vaiheeseen, jossa matriisimekaniikka saa näyttää kyntensä. Schrödingerin yhtälöä (1) modifioidaan ajasta riippuvaksi, joka mahdollistaa neutraalin kaonin ”oskillaation” kahden tilan a ja b välillä. Kuvan 1 Feynmanin diagrammin kuvaama tapaus eroaa kirjoitukseni alussa mainitusta (yhden hiukkasen) kaksitilasysteemistä siinä, että mesoni on kaksihiukkassysteemi, jossa oskillaatio voidaan selittää kvarkkien tasolla. Neutraalin antikaonin s-kvarkki absorboi ensin W+-hiukkasen ja sitten W–-hiukkasen, jolloin se vaihtaa kaksi kertaa lajia ja siitä tulee d (välivaiheena on u, c tai t). Samaan aikaan (kuvassa oikealle kulkevan puolijakson aikana) anti-d muuttuu kahden W-hiukkasen emission kautta anti-s:ksi. Kuvassa vasemmalle kulkevan puolijakson aikana W-hiukkasten absorptiot ↔ emissiot.
$$\mathrm{\Psi}\left(t\right)=U\left(t\right)\mathrm{\Psi}\left(0\right)=e^{iHt}\binom{a}{b} \qquad \qquad \qquad \qquad \qquad (5)$$
Systeemin ”hamilton” eli H-matriisi on 2×2 matriisi, jonka alkiot ovat reaaliset silloin, kun CP oletettavasti säilyy. Neljä alkiota ovat pareittain identtiset: kaksi (diagonaalista) tulee vahvasta ja kaksi muuta heikosta vuorovaikutuksesta. Diagonaaliset alkiot pitävät huolen siitä, että kaonilla ja antikaonilla on sama massa, kaksi muuta huolehtivat oudon ja antioudon tilan sekoittumisesta. Matriisin diagonalisointi tuottaa halutut ominaistilat (ei tehdä diagonalisointia tässä vaan käytetään a priori -tietoa ominaistilojen kirjoittamiseen samaan tapaan kuin spinien kytkeytymisessä edellä).
Kirjoitetaan superpositiot
$\left.\left|K_1\right.\right\rangle=\frac{1}{\sqrt2}\left(\left.\left|d\bar{s}\right.\right\rangle\ +\left.\ \left|\bar{d}s\right.\right\rangle\right)$ ja
$\left.\left|K_2\right.\right\rangle=\frac{1}{\sqrt2} (\left.\left|d\bar{s}\right.\right\rangle – \left.\left|\bar{d}s\right.\right\rangle)$, joissa
$|d \bar{s} \rangle=|K^0\rangle$ ja $|\bar{d}s\rangle={\bar{K}}^0\rangle \qquad \qquad \qquad \qquad \qquad (6)$
Ominaistiloista K1 ja K2 huomataan välittömästi, että ensimmäinen niistä on hiukkas–antihiukkasvaihdon eli CP-operaation suhteen symmetrinen ja toinen on antisymmetrinen. Käytännössä tämä tarkoittaa CP-symmetrian vallitessa sitä, että tila K1 (jonka ominaisarvo CP = +1) voi hajota kahdeksi hiukkaseksi (joilla CP = +1) siinä missä tila K2 (jonka ominaisarvo CP = -1) voi hajota kolmeksi hiukkaseksi (joilla CP = -1). Nämä hajoamismoodit esitetään MAOLin taulukkokirjan hadronitaulukossa siten, että lyhytikäinen KS=K1 ja pitkäikäinen KL=K2. Näin huomataan, että alun perin Paulin kieltosäännön ja elektronisen spinaaltofunktion symmetriaominaisuuksien kuvaamiseen kehitetty tekniikka soveltuu paitsi ydinspinien myös nukleonien ulkopuolisesta kvarkkimaailmasta esiin nousevan “oudon” mesonin hiukkas–antihiukkassymmetrian kuvaukseen. Äärimmäisen mielenkiintoiseksi neutraalin kaonin hajoaminen nousi vuonna 1964, kun Princetonin yliopiston tutkijaryhmä Brookhavenin laboratorion kiihdytinkokeissa havaitsi, että KS ja KL ovatkin vain lähes-ominaistiloja (tai ”heikkoja” ominaistiloja) ja CP-symmetria täten vain melkein-symmetria. Myöhemmin uusilla kokeilla varmennetuista löydöistään James Cronin ja Val Fitch palkittiin fysiikan Nobelilla vuonna 1980. Croninin ja Fitchin havaitseman epäsuoran symmetriarikon vuoksi kirjoitetaan uudet superpositiot
$K_L={{\varepsilon K}_1+K}_2$ ja
$K_S=K_1+{\varepsilon K}_2$, joissa $\left|\varepsilon\right|\cong0,002$ [3] $\qquad \qquad \qquad \qquad \qquad (7)$
2000-luvulla CP-rikko on verifioitu myös raskaammilla B- ja D-mesoneilla, joista ensimmäinen sisältää b-kvarkin ja toinen c-kvarkin. Aktiivista tutkimusta tehdään tällä hetkellä muun muassa sen kysymyksen parissa, havaitaanko CP-rikko myös neutriinojen oskillaatioissa? Matriisimekaniikkaan perehtyvälle teoreettisen hiukkasfysiikan harrastajalle poimin lisäksi pari kysymystä fysiikan ratkaisemattomien ongelmien listalta: Miksi vahva ydinvoima on CP-invariantti? Miksi universumissa on materiaa niin paljon enemmän kuin antimateriaa? Sekä nukleonisynteesin vaiheiden yksityiskohtainen selvittäminen.
Viitteet
[1] Max Born ja Werner Heisenberg, ”Quantum mechanics”, viidennen Solvay-konferenssin asiakirjat. Leiden, 1927.
[2] Carlo Rovelli, Helgoland, käännös italiasta englantiin Erica Segre ja Simon Carnell, Allen Lane/ Penguin Random House UK, 2021.
[3] Stuart Coleman, The Fitch-Cronin Experiment, kurssityö, 2008. Verkossa http://large.stanford.edu/courses/2008/ph204/coleman1/







