Murtoluvulla jakamisen malleja
Murtoluvulla jakamista pidetään joskus vaikeana ideana. Jakolaskun oppiminen on kuitenkin paljon helpompaa, jos murtoluvun käsite on hyvin hallussa ja jakamista on pohjustettu mallein ja esimerkein ennen laskutoimituksen opettamista.
Kirjan Ymmärrä matematiikkaa [1] tekijät Anne Lene Johnsen ja Elin Natås sanovat, että ”murtolukujen jakaminen on tavattoman abstraktia toimintaa, jota voi olla vaikea selittää lapselle – – murtoluku jaetaan toisella murtoluvulla kertomalla ensimmäinen toisen käänteisluvulla. Murtoluvusta tehdään käänteisluku kiepauttamalla se ylösalaisin”. Ei siis yritystäkään ymmärtämisen suuntaan.
Varga–Neményi-kirjojen tekijä Anni Lampinen sanoo kokemuksensa perusteella, että ”menetelmään kuuluu hidas ja perusteellinen käsitteen pohjustaminen, jolloin laskutoimitusten opettamista viivästytetään niin paljon kuin se suinkin on mahdollista. Jos lukuja tunnetaan monipuolisemmin ja syvällisemmin, niin peruslaskutoimitukset on sitten aikanaan nopeasti opittu, koska samat aritmeettiset periaatteet pätevät myös uudessa ympäristössä. Laskemista kokeillaan ja harjoitellaan sekä todetaan, ettei tässä nyt sitten ole mitään niin ihmeellistä uutta.” Pohjustaminen sisältää monenlaisia malleja ja konkreettisia tilanteita ennen laskemista pelkillä luvuilla. Murtolukuja opetellaan yhdistyksen oppikirjasarjassa vähitellen kouluvuosina 3–6. Hidasta etenemistä tukevat nykyiset perusopetuksen opetussuunnitelman perusteet, joissa murtoluvun jakaminen murtoluvulla on siirretty yläluokille.
Jakolaskujen piirrosmalleja
Perusesimerkki murtoluvulla jakamisesta voisi olla tarinapaperin [2] kuva luvun kaksi jakamisesta luvulla $\frac{1}{3}$ (kuva 1). Tulos näkyy suoraan kuviosta ilman mitään laskutoimitusta. Pienellä apuvärityksellä voidaan samasta kuviosta nähdä vastaus myös jakamiseen luvulla $\frac{2}{3}$.
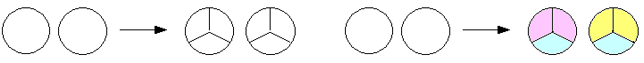
Malli näyttää kovin alkeelliselta, mutta se soveltuu monimutkaisempiinkin tapauksiin, vaikkakin piirtäminen saattaa suurempien lukujen kohdalla olla vähän työlästä käsin piirrettäessä. Esimerkiksi jakolasku $7:\frac{5}{6}$ näyttää tältä (kuva 2). Kyseessä on selvästi sisältöjako.

Ympyrämalli toimii myös silloin, kun jaettavakin on murtoluku, mutta ei ole monimutkaisuutensa takia enää yhtä havainnollinen. Toisaalta se on hyvin tehokas, sillä samasta mallista saa vastauksen sekä laskuun $\frac{2}{3}:\frac{4}{5}$ että laskuun $\frac{4}{5}:\frac{2}{3}$ (kuva 3). Kyse onkin ehkä enemmän lukujen vertaamisesta kuin varsinaisesta jakolaskusta, mutta tuloshan on sama ja kertoo vain murtoluvun erilaisista merkityksistä [3].
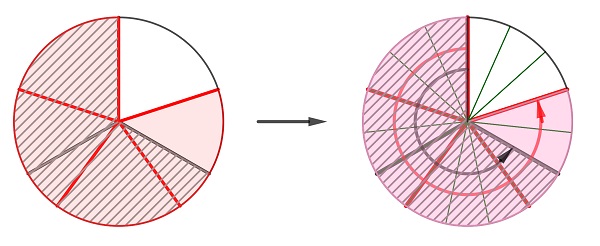
Malli vastaa tavanomaisesta poikkeavaa jakolaskualgoritmia
$\frac{2}{3}:\frac{4}{5}=\frac{10}{15}:\frac{12}{15}=10:12=\frac{5}{6}$
Samannimisiksi laventamiseen perustuva murtolukujen jakolaskutapa voisi olla ymmärrettävämpi kuin tavanomainen kertolaskuksi muuttaminen, vaikka se ei olekaan aina yhtä tehokas.
Tämä laskutapa (algoritmi) on helposti ymmärrettävä, koska sen perusidea on sama kuin laatulukujen (suureiden arvojen) vertaamisessa kokonaisluvuilla laskettaessa:
1 km : 200 m = 1000 m : 200 m = 1000 : 200 = 5.
Verrattaessa suureiden arvoja ne pitää muuntaa samoiksi yksiköiksi ennen jakolaskua, mikä vastaa samannimisiksi laventamista.
Muita malleja
Yksikköympyrään tai -ympyröihin perustuva piirrosmalli on hyvin havainnollinen yksinkertaisissa tapauksissa. Oppimisen kannalta se on ehkä jopa liiankin helppo, sillä yksikkö(ympyrä) pysyy koko ajan samana, ympyröiden määrällä ei ole mitään rajaa eikä myöskään sillä, kuinka moneen osaan ympyrä voidaan jakaa.
Konkreettisilla välineillä ei saa (ainakaan helposti) mallinnetuksi kaikkia murtolukujen jakamisia. Ongelman voi kääntää eduksi asettamalla tehtävän niin, että on keksittävä jakolaskutehtäviä, jotka voi tehdä annetuilla välineillä. Tai sitten voi ottaa käyttöön useamman sarjan murtokakkuja tai leikata pahvista avuksi useampia yksikkökiekkoja tai muita kuin yksikkömurtolukuja.
Värisauvat tuovat vielä uuden haasteen, sillä yksikkökuutiota ei voi jakaa. Ongelma ei ole ratkaisematon. Pitää vain laventamista vastaten vaihtaa ykkösen esittämistapaa. Esimerkiksi kuvan 1 jakolaskut pystyy mallintamaan pitämällä kolmossauvaa ykkösenä. Silloin ykkössauva (kuutio) tarkoittaa lukua $\frac{1}{3}$ ja kakkossauva lukua $\frac{2}{3}$. Tulos on luettavissa mallista (kuva 4). Värinapeilla malli on vielä yksinkertaisempi, mutta vaatii ehkä vähän enemmän suunnittelua ja päämäärän hahmottamista, sillä jo mallin rakentamisen alkuvaiheessa on päätettävä, kuinka monen värinapin ryhmä edustaa lukua 1.

Lukusauva- ja värinappimallit eivät oikeastaan ole mitenkään erityisesti jakolaskun malleja. Esimerkiksi kuvan 4 alemman rivin oikeanpuolinen malli voi – yhtä hyvin kuin jakolaskua – edustaa luvun 2 murtolukuhajotelmaa
$2=\frac{2}{3}+\frac{2}{3}+\frac{2}{3}$
tai kertolaskua
$2=3\cdot\frac{2}{3}$.
Kyse on vain siitä, mitä mallin ajatellaan esittävän. Onko tehtävänä ’esitä luku 2 lukujen $\frac{2}{3}$ summana’, ’millä luvulla luku $\frac{2}{3}$ on kerrottava, jotta tulo on 2’ tai ’kuinka monta kertaa luku $\frac{2}{3}$ sisältyy lukuun 2’. Mallin rakentamiseen ja tulkintaan tarvitaan siksi vahvaa murtoluvun käsitettä ja valmiutta joustavaan ajatteluun.
Paljaiden lukujen jakolaskut syventävät vain yhtä puolta murtoluvun käsitteen merkityksistä. Muiden puolien, kuten esimerkiksi objekti, operaatio tai suhde [3], esille tuomiseen tarvitaan mallien lisäksi konkreettisia tilanteita ja sovellustehtäviä, kuten esimerkiksi suureiden suhteita sanallisissa tehtävissä. Tällaisten tehtävien työstämiseen sopii mainiosti alussa mainittu tarinapaperi [2].
Päivitys 3.1.2021
Paula Anttilalla on paljon hienoja murtolukujen laskutoimitusten havainnollistuksia Geogebra-materiaaleissa osoitteessa https://www.geogebra.org/search/murtoluku%20Anttila
Erityiskiitoksen tästä jutusta ansaitsee Varga–Neményi-yhdistyksen toiminnanjohtaja Anni Lampinen, jolta olen saanut paljon tietoja ja ennen kaikkea virikkeitä jutun kehittelyyn.
Lähteitä ja lisää luettavaa:
[1] Johnsen, A. L. ja Natås, E.: Ymmärrä matematiikkaa. 23-metodilla menestykseen. Bazar, Helsinki 2018.
Esittely Dimensio-lehdessä https://www.dimensiolehti.fi/kirjallisuutta-ymmarra-matematiikkaa/
[2] Ikäheimo, H. ja Voutilainen, E. Tee, piirrä, kerro ja ymmärrä!, sivulla http://opperi.fi/02_opetusvinkkeja/2211_tarinapaperi.html
[3] Katso esimerkiksi
Mäki, N. ja Vihelä, E.. 2019. Kumpi on suurempi, puolet kolmasosasta vai kolmasosan puolikas? Murtolukukäsitteen opettaminen kolmessa kolmannen luokan oppikirjassa, s. 41–43. Kasvatustieteen pro gradu -tutkielma. Jyväskylän yliopisto. Kokkolan yliopistokeskus Chydenius, 2019. Saatavissa osoitteesta https://drive.google.com/file/d/1nLmA6Gw_ppIxAdfJLf7FT7-xBRriLdL1/view?usp=drivesd







