Päässälaskuja peruskoulussa

Päässälaskujen laskeminen on erinomainen tapa oppimisen tai oppimatta jäämisen osoittamiseen sekä taitojen varmistamiseen ja ylläpitämiseen. Se voidaan tehdä monella tavalla. Myös niin, että oppilaat osallistuvat sekä tehtävien tekemiseen että esittämiseen. Kauan sitten opettajana ollessani toimin peruskoululaisten kanssa näin. Idea on nyt tarjolla MAOLin jäsenillassa 23.4.2024.

Jokaisen tunnin alussa oli lyhyt päässälaskutuokio: viisi laskua, joiden tavoitetaso oli neljä oikein viidestä keskimäärin. Tehtävät olivat oppilaiden tekemiä. Kukin oppilas keksi kotona sarjan ja myös esitti sen. Vuoro kiersi riveittäin luokassa niin, että kaikki pääsivät mukaan. Ei haitannut mitään, vaikka vuoro unohtui, sillä aina jollakin muulla oli sarja valmiina. Ja jos ei ollut, niin opettaja sellaisen tekaisi paikan päällä; tätä tapahtui kyllä kovin harvoin.

Aiheet vaihtelivat aikaisemmin opitun varmentamisesta juuri opittavina oleviin laskutaitoihin. Erityisesti laskujärjestyksellä, nollalla kertomisella ja muilla sellaisilla kikoilla oppilaat pystyivät luomaan mahdottomilta näyttäviä tehtäviä, joihin kuitenkin oli ymmärtävälle helppo ja suoraviivainen ratkaisu. 

Tehtävien tekijä kirjoitti tehtävät tauluun yksi kerrallaan. Oppilaat laskivat päässä, jos pystyivät, paperiakin sai käyttää apuna; hyvin vähän käytettiin. Lopuksi esittäjä kirjoitti vastaukset näkyviin ja oppilaat laskivat itselleen pistemäärän. Sen jälkeen tarkastettiin, että vastaukset olivat oikein, ja laskettiin näkyviin ne, joita joku ei ollut osannut tai joiden vastaus asetettiin kyseenalaiseksi. Lopuksi piirrettiin histogrammi tuloksesta sen mukaan, kuinka monta kättä nousi kunkin pistemäärän kohdalla. 

Oikeasta vastauksesta keskusteleminen oli usein jakson parasta antia, vaikka tavoitteena olikin varsinaisesti harjoitella päässälaskemista. Oheistuloksina oppilaat pääsivät näyttämään, mitä itse osaavat, ja oppivat näkemään, mitä muut osaavat, sekä tarkkailemaan toisten työskentelyn edistymistä, ja tietysti tottumaan luokan edessä esiintymiseen. Seuraavista jakaumista näkyy, että oppilaat pystyivät monessa tapauksessa arvioimaan luokan osaamisen tasoa melkoisen hyvin. 

Aikaahan tähän kului, mutta se korvattiin jättämällä muu läksynkuulustelu pois. Päässälaskutuokiot korvasivat sen mielestäni hyvinkin. Näin pitkän aikaa jälkeenpäin katsottuna päässälaskutuokiot eivät palvelleet yksinomaan oppimisen seuraamista, vaan niillä oli olennainen merkitys oppilaiden kasvattamisessa aktiiviseen osallistumiseen ja erityisesti avoimen ja keskustelevan ilmapiirin luomisessa, mikä heijastui sitten koko luokkaopetukseen. 

Artikkelikuvassa nämä päässälaskujen tekijät poseeraavat spontaanisti kesken oppitunnin. Kuva julkaistiin myöhemmin virolaisen Haridus-lehden kansikuvana numerossa 9/2005.

Kasin päässälaskuja, Jokivarren koulu 8b, 2004

Aino

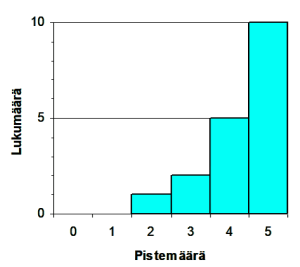
1. 1,2 + 0,08 + 0,36

2. 3 – 1,356

3. Laske keskiarvo: 2, 2, 3, 3, 5

4. (5a + 6b + 13a) : 3

5. 255,68 · 1000

Eero

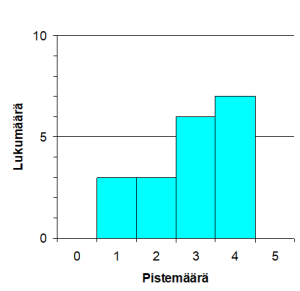
1. 8 · (2360 + 5656) – 7 · (2360 + 5656)

2. 2x² · 7x² + 27x – 13x² – 26x

3. – 35 · 2 + 35 : 2

4. (3560 + 5068 – 4743 · 10 + 57) · 0

5. 3750 + 249 : 3 : 3 : 3 : 3

Eevi

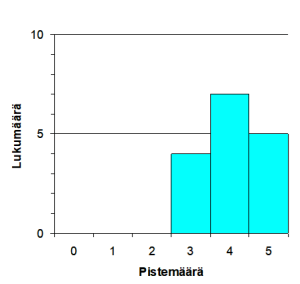
1. 100 – 2 + 600

2. x + 2x + 1,5x

3. 5s – 2s · 6

4. 8 · 5 + (6 · 2)

5. 6 · 6 · 4 + 2

Hanna

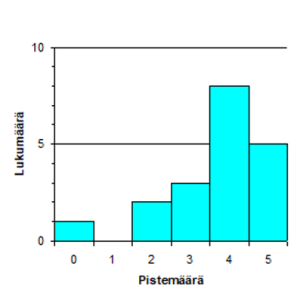
1. (–18x – 9) · 2

2. Mikä on x?

87 953 · 8 – 87953 · x = 87953

3. –98,8 – 17,2

4. 0,0807 : 1 000 000 · 100

5. (5a + 8b + 5,5a + 2,5b) : 5

Janina

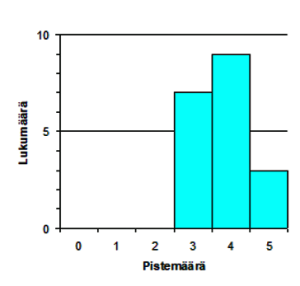
1. $\frac{4x^{2}-8n+14h}{2} + 2x^{2} + n -h$

2. $2(3a+4b+3b)$

3. $2 ⋅ 5a+2a ⋅ 2a$

4. $a+b+a- (-a-a+b)$

5. $\frac{-6a + 8 + 4b}{2} $

Minna

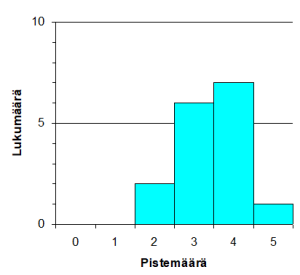
1. 5 · (–3 + 2 + ( –3))

2. 2  –  ( –2 + 12)

3. $1\frac{1}{2}-(–13-14)$

4. 93  –  (12a + 3) · 2

5. 9²– 2 ⋅ 3

Teemu

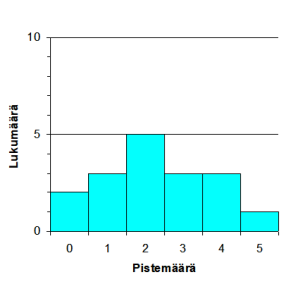
1. (3³ – 2) + 2 ꞏּ 12 : 2

2. (2 133 + 10 000) ꞏ 10 ּ 2^x = 484 920

3. 6736 ּ 7 – 6736 · 8 : 2 · 1

4. 2² + 3² + 4² + 5² – 6²

5. (2x + 100x) – (–2x + -100x)

Vesku

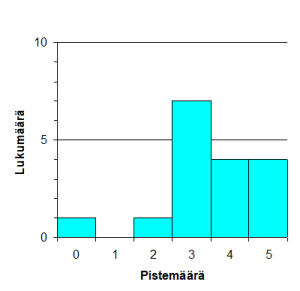
1. 5x + 6x · 10 + 21

2. 10x + 4x – ( 3x – 3)

3. 7a · 4a – (–3a + 4a · 5a – 10b)

4. 3³+4³+ (-25)

5. 10 – 10 · 10 – 10