Pallon kelluminen – esimerkki kolmannen asteen yhtälöstä
Johdanto
Toisen asteen yhtälöön päädytään monissa fysiikan ongelmissa. Kolmannen asteen yhtälö sen sijaan tulee vastaan harvemmin yksinkertaisissa fysiikan sovelluksissa. Ehkä tunnetuin tapaus on reaalisia kaasuja (ideaalikaasun tilayhtälöä paremmin) kuvaava van der Waalsin tilayhtälö, jonka viriaalikehitelmän avulla paine voidaan lausua kolmannen asteen polynomina tiheydestä (kts. esimerkiksi [1]).
Tarkastellaan tässä toista yksinkertaista esimerkkiä, pallo-symmetrisen kappaleen kellumista. Olkoon pallon säde $r$ ja pallon keskimääräinen tiheys $\rho$. Pallo kelluu nesteessä, jonka tiheys on $\rho_0$. Pallon paino ja nesteen aiheuttama noste ovat kellumisessa tasapainossa:
$$\frac{4\pi}{3}r^3\rho\ g=\ \frac{\pi}{3}\left(4r^3-3rh^2+h^3\right)\rho_0\ g \; \; \; \; (1)$$
jossa on käytetty pallon ja pallokalotin tilavuuksien lausekkeita, ks. [2]. Sievennettynä tästä saadaan kolmannen asteen yhtälö korkeudelle $h$, joka pallosta on nestepinnan yläpuolella:
$$h^3-3rh^2+4r^3\left(1-\frac{\rho}{\rho_0}\right)=0 \; \; \; \; (2)$$
Käytetään merkintöjä: $c=\ \rho/\rho_0$ ja $x=h/r$. Saamme yhtälön $x$:lle
$$x^3-3x^2+4\left(1-c\right)=0 \; \; \; \; (3)$$
Jotta pallo kelluisi, pallon tiheys saa olla korkeintaan nesteen tiheys, eli: $1\geq\ c>0$. Tällöin nestepinnan yläpuolella olevan osan korkeudelle pätee: $0\le\ h<2r$. Toisin sanoen fysikaalinen alue muuttujalle $x$:lle on: $0\le\ x<2$.
Funktion
$$f\left(x\right)=x^3-3x^2+4\left(1-c\right) \; \; \; \; (4)$$
käännepisteet löytyvät derivaatan nollakohdista:
$$0=f^\prime\left(x\right)={3x}^2-6x\ \ \rightarrow\ x=0\ ja\ x=2 \; \; \; \; (5)$$
Näemme, että $f\left(0\right)=\ 4\left(1-c\right)\ \geq0$ ja $f\left(2\right)=\ -4c<0$. Kun $0<c<1$ on yhtälöllä (3) siten kolme reaalista ratkaisua, joista yksi sijoittuu fysikaaliselle välille $0<x<2$, kahden muun ratkaisun ($x<0$ ja $x>2$) ollessa epäfysikaalisia.. Rajatapauksessa $c=1$ (pallon tiheys on sama kuin nesteen tiheys), on yhtälöllä (3) kaksoisjuuri, $x=0$, mikä vastaa tilannetta, jossa pallo on kokonaan nestepinnan alapuolella. (Kolmas ratkaisu on epäfysikaalinen, $x=3$.)
Rajalla $c\rightarrow0$ (massaton pallo) yhtälöllä (3) on kaksoisjuuri, $x=2$ vastaten tilannetta, joissa pallo olisi kokonaan nestepinnan yläpuolella. (Tässäkin rajatilanteessa kolmas juuri on epäfysikaalinen, $x=-1$.)
Kolmannen asteen yhtälö
1500-luvulla Scipione del Ferron, Niccolo Tartaglian ja Gerolamo Cardanon kehittämä kolmannen yhtälön ratkaisutapa lähti sijoituksesta, jolla poistetaan yhtälöstä toisen asteen termi. Esimerkki tapauksessamme tämä sijoitus olisi $x = z+1$, jolloin yhtälö tulee olemaan muotoa
$$z^3+pz+q=0 \; \; \; \; (6)$$
jossa nyt käsillä olevassa tapauksessa $p=\ -3$ ja $q=2(1-2c)$. Yhtälön (6) yleinen ratkaisu on (kts. esim. [3]).
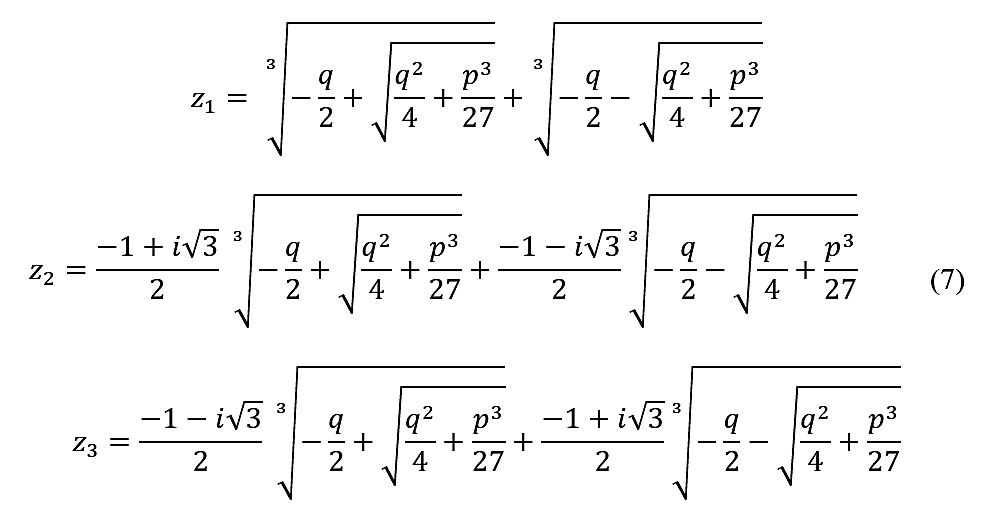
Sijoittamalla edeltä esimerkkimme $q$:n ja $p$:n arvot, näemme, että
$$\sqrt{\frac{q^2}{4}+\frac{p^3}{27}}=\ \sqrt{4c^2-4c}=\pm2i\sqrt{c\left(1-c\right)} \; \; \; \; (8)$$
koska $c\le1$. Voimme siten kirjoittaa alkuperäisen yhtälömme (3) ratkaisut:
$$x_1=1+\sqrt[3]{2c-1+2i\sqrt{c\left(1-c\right)}}+\ \sqrt[3]{2c-1-2i\sqrt{c\left(1-c\right)}} \; \; \; \; (9)$$

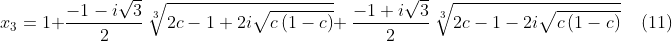
Näissä ratkaisuissa näkyy yleinen kolmannen asteen yhtälön ratkaisukaavan piirre: reaaliset ratkaisut ovat lausuttavissa kahden kompleksisen liittoluvun summana.
Ratkaisuista (9–11) $x_1>2$ ja $x_2<0$ (riippumatta $\ c$:n arvoista välillä $0<c<1$). Viimeiselle ratkaisulle pätee: $0<\ x_3<2$, eli tämä ratkaisu on yhtälön (3) fysikaalinen ratkaisu.
Katsotaan ensin tarkistuksen vuoksi tapaus $c\ =\frac{1}{2}$ (vastaten siis tilannetta, jossa pallon tiheys on puolet nesteen tiheydestä. Tällöin
$$\sqrt[3]{2c-1\pm2i\sqrt{c\left(1-c\right)}}=\sqrt[3]{\pm i}=\ \sqrt[3]{e^{\pm i\pi/2}}=\ e^{\pm i\pi/6} \; \; \; \; (12)$$
Käyttäen Moivren kaavaa saamme
$$e^{\pm i\pi/6}=\ \cos{\frac{\pi}{6}}\ \pm\ i\sin{\frac{\pi}{6}}=\ \frac{\sqrt3}{2}\pm\frac{i}{2} \; \; \; \; (13)$$
jolloin
$$x_3=1+\frac{-1-i\sqrt3}{2}\left(\frac{\sqrt3}{2}+\frac{i}{2}\right)+\ \frac{-1+i\sqrt3}{2}\left(\frac{\sqrt3}{2}-\frac{i}{2}\right)=1 \; \; \; \; (14)$$
Tarkoittaen, että pallo on puoliksi nesteessä kuten tulee ollakin, jos pallon tiheys on puolet nesteen tiheydestä.
Algebrallinen ratkaisumuoto (11) on (kahden kompleksisen liittoluvun summana) hieman epäkäytännöllinen tarkoitukseemme. Lausutaan kuutiojuuressa oleva lauseke kompleksiluvun normin ja suuntakulman avulla. Huomataan, että normi on tässä esimerkkitapauksessamme ykkönen:
$$\left|2c-1\pm2i\sqrt{c\left(1-c\right)}\right|=\ \left(2c-1\right)^2+4c\left(1-c\right)=1 \; \; \; \; (15)$$
Tällöin
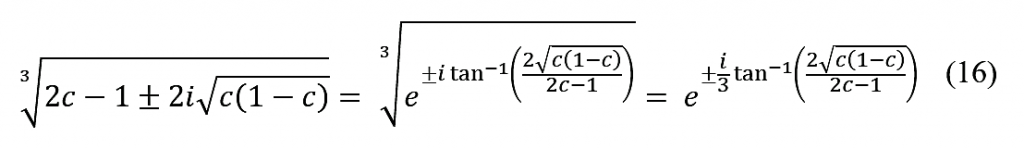
jossa $0\le\tan^{-1}{\left(\frac{2\sqrt{c\left(1-c\right)}}{2c-1}\right)}\le\pi$. Yhteensä (taas Moivren kaavaa käyttämällä) saamme ratkaisun trigonometristen funktioiden avulla:
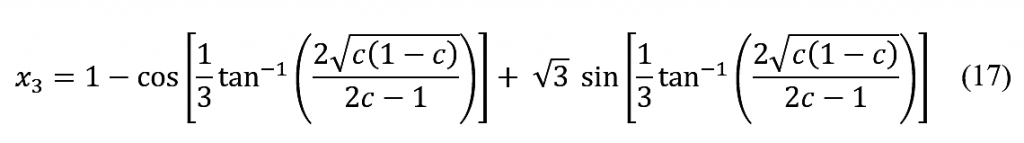
Kirjoitetaan tämä vielä vähän eri muotoon. Olkoon
$$\alpha=\cos^{-1}{\left(2c-1\right)}\ \ ,\ \ \ \ 0\le\alpha\le\pi \; \; \; \; (18)$$
Tällöin (etumerkkeineen, koska $\sin{\alpha}\geq0$ alueessa $0\le\alpha\le\pi$)
$$\tan{\alpha}=\frac{\sin{\alpha}}{\cos{\alpha}}=\ \frac{\sqrt{1-\cos^2{\alpha}}}{\cos{\alpha}}=\ \frac{2\sqrt{c\left(1-c\right)}}{2c-1} \; \; \; \; (19)$$
Eli voimme kirjoittaa ratkaisun yhtälössä (17):
$$x_3=1-\cos{\left[\frac{1}{3}\cos^{-1}{\left(2c-1\right)}\right]}+\ \sqrt3\ \sin{\left[\frac{1}{3}\cos^{-1}{\left(2c-1\right)}\right]} \; \; \; \; (20)$$
tai edelleen
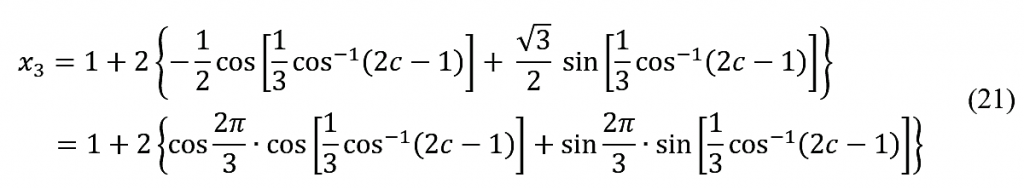
Käyttämällä kosinin yhteenlaskukaavaa tämän voi vielä kirjoittaa mahdollisimman yksinkertaiseen muotoon:
$$x_3=1+2\cos{\left[\frac{2\pi}{3}-\ \frac{1}{3}\cos^{-1}{\left(2c-1\right)}\right]} \; \; \; \; (22)$$
Ratkaisu trigonometristen yhtälöiden avulla
Kolmannen asteen yhtälöitä voi ratkaista myös trigonometristen yhtälöiden avulla, kuten Francois Viete myöhemmin 1500-luvun lopulla osoitti, ks. [4]. Merkitään yhtälössä (6), (jossa $p=\ -3<0$)
$$z=2\sqrt{\frac{-p}{3}}\ \cos{\varphi} \; \; \; \; (23)$$
Yhtälö (6) tulee tällöin muotoon
$$2\left(\frac{-p}{3}\right)^{3/2}\left(4\cos^3{\varphi}-3\cos{\varphi}\right)+q=0 \; \; \; \; (24)$$
Eli
$$2\left(\frac{-p}{3}\right)^{3/2}\cos{3\varphi}+q=0 \; \; \; \; (25)$$
Missä on käytetty hyväksi kolminkertaisen kulman kosinin lauseketta. Trigonometrisen yhtälön (25) ratkaisu on
$$\varphi=\pm\left[\frac{1}{3}\cos^{-1}{\left(-\frac{q}{2\left(\frac{-p}{3}\right)^{3/2}}\right)}\right]+\frac{2n\pi}{3} \; \; \; \; (26)$$
$n=0,1,2$. Tällöin yhtälön (30) perusteella
$$x=1+z=\ 1+2\sqrt{\frac{-p}{3}}\ \cos{\left(\pm\frac{1}{3}\cos^{-1}{\left(-\frac{q}{2\left(\frac{-p}{3}\right)^{3/2}}\right)}+\frac{2n\pi}{3}\right)} \; \; \; \; (27)$$
jossa sijoituksella $p=\ -3$ ja $q=2(1-2c)$ fysikaalinen ratkaisu, yhtälö (22), saadaan, kun valitaan negatiivinen etumerkki ja $n=1$. Tämä on kosinin parillisuuden nojalla sama kuin jos valitaan positiivinen etumerkki ja $n=2$, kun kosinin argumentista vähennetään vielä $2\pi$.
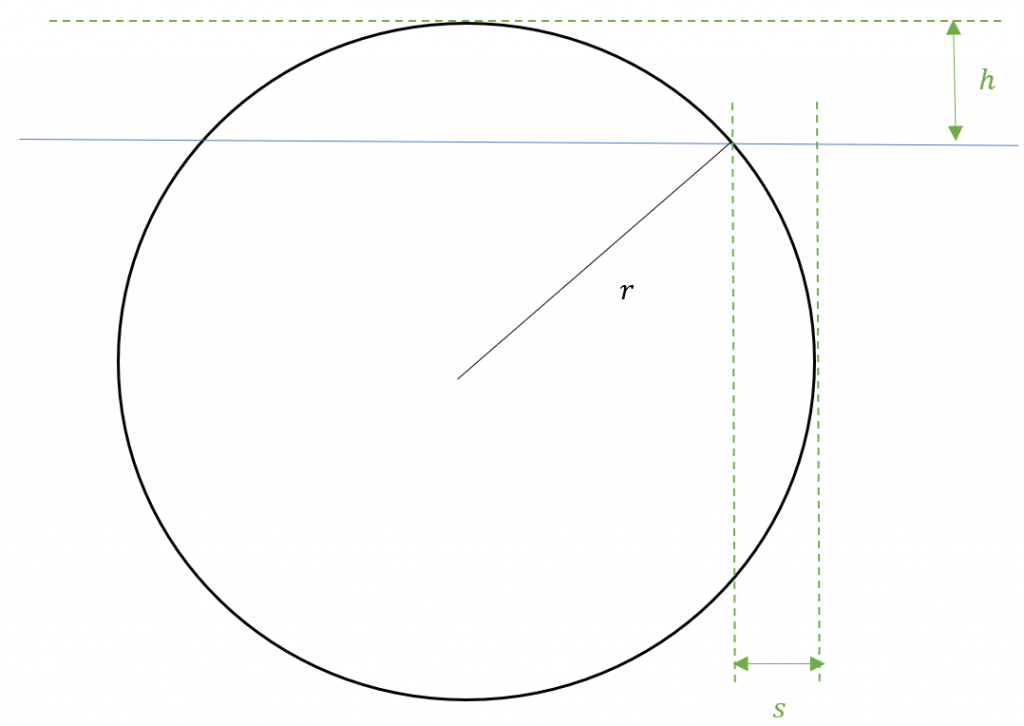
Pallomainen jäävuori
Sovelletaan nyt ratkaisuamme, yhtälöä (22), pallomaisen jäävuoren tarkastelemiseen. Jään tiheyden, $\rho=917\frac{kg}{{m\ }^3}$, ja suolaisen valtameren veden tiheyden, $\rho_0=1020\frac{kg}{{m\ }^3}$, perusteella $c=0,8990$. Tällöin yhtälöstä (22) $x=\ x_3=0,3937$.
Kuvan 1 perusteella saamme laskettua etäisyyden, minne asti pallomainen jäävuori ulottuu pinnan alla sivusuunnassa:

eli tämä pallomaisen jäävuoren sivusuuntainen ulottuvuus pinnan alla on vähän yli puolet pinnan yläpuolisesta korkeudesta.
Lähdeviitteet
[1] Marcelo Alonso & Edward J. Finn, Physics, Addison Wesley, 1992
[2] Raimo Seppänen, Leena Mannila, Martti Kervinen, Irma Parikka, Pasi Konttinen, Lea Karkela ja Tuomas Yli-Kokko, MAOL:n taulukot, MAOL ja Kustannusosakeyhtiö Otava, 2013
[3] Milton Abramowitz, Irene A. Stegun; Handbook of Mathematical Functions, Dover Publications Inc, New York, 1970
[4] https://en.wikipedia.org/wiki/Cubic_equation
Tilaa Dimension uutiskirje – saat sähköpostiisi aina kuunvaihteessa koosteen tuoreimmista artikkeleista







