Piin laskemisen historiaa

Tiede ja teknologia

14.3.2022

Tänään on piin päivä, kansainvälinen matematiikan päivä ja myös Albert Einsteinin syntymäpäivä. Piin päivää vietetään 14 maaliskuuta, koska piin likiarvo on 3,14. Tässä artikkelissa käymme läpi piin arvon laskemisen historiaa.

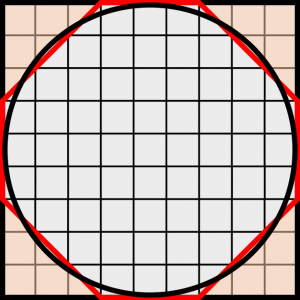
Pii π tarkoittaa ympyrän kehän suhdetta halkaisijaan. Jo muinaiset babylonialaiset ja egyptiläiset tutkivat ympyrän kehän suhdetta halkaisijaan. Ensimmäiset kirjalliset merkinnät piistä löytyvät Egyptistä vuodelta 1650 eaa Rhindin papyryksesta, jonka on kirjoittanut kirjuri Ahmesi. Piin määritys perustui havaintoon, että ympyrän pinta-ala on lähellä 8-kulmion pinta-alaa. Kuvasta 1 havaitaan, että 8-kulmion pinta-ala saadaan laskettua, kun 9×9 neliöstä vähennetään neljä 3×3 nurkkakolmiota pois.

$$9^{2}-4\cdot \frac{3\cdot 3}{2} = 81 -18 = 63 \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (1)$$

Koska 8-kulmion pinta-ala 63 voidaan pyöristää ylöspäin lukuun 64, niin saadaan ympyrän pinta-alaksi 8×8 neliön pinta-ala. Egyptiläiset totesivat ympyrän pinta-alan olevan sama kuin sellaisen neliön, jonka sivu on 8/9 ympyrän halkaisijasta. Kuvasta 1 havaitaan, että ympyrän säde on 4,5 ruutua, jolloin voimme laskea egyptiläisten arvion piille seuraavasti.

$$\pi\ r^2=A\ \Longleftrightarrow\ \pi=\frac{A}{r^2}=\frac{64}{{4,5}^2}={\frac{64}{20,25}}^{(4}=\frac{256}{81}\approx3,1605 \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (2)$$

81 pieneen neliöön jaettu neliö ja sen sisälle piirretty ympyrä, piin laskemisen historiaa — Kuva 1: Egyptiläiset arvioivat piin arvon piirtämällä 9×9 neliön sisälle 8-kulmion, jonka pinta-alaksi arvioitiin 64. Koska neliön pinta-ala on 9² ja ympyrän pinta-ala on 8², niin voidaan todeta, että pätee sääntö $\pi \cdot 4,5^{2}= 64$.

Piin laskeminen antiikin Kreikassa

Antiikin kreikassa osattiin laskea piille jo tarkempi arvo. Kreikkalaiset piirsivät ympyrän sisälle säännöllisen kuusikulmion ja ympyrän ulkopuolelle säännöllisen nelikulmion eli neliön (Kuva 2). Säännöllinen kuusikulmio koostuu kuudesta tasasivuisesta kolmiosta. Jos laitamme ympyrän halkaisijaksi 1, niin kuvasta on helppo päätellä, että neliön piiri on neljän ympyrän halkaisijan mitta ja säännöllisen kuusikulmion piiri on kolmen ympyrän halkaisijan mitta. Koska ympyrän kehä on pii kertaa halkaisija, niin tästä voimme päätellä, että piin arvo on kolmea suurempi ja nelosta pienempi. Piin arvo tarkkenee, kun muutamme kuusikulmion tilalle 12-kulmion, 24-kulmion, 48-kulmion jne.

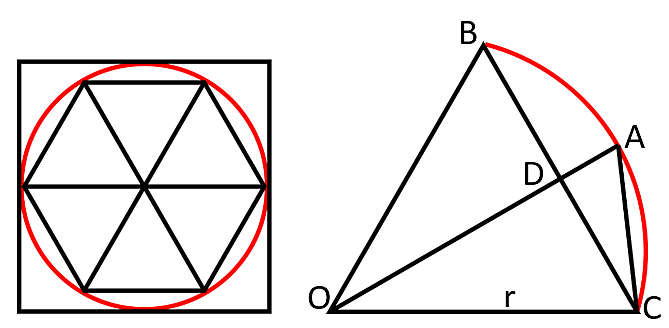
Kuva 2: Kreikkalaiset selvittivät piin arvon säännöllisen monikulmion kehän pituuden avulla.

Arkhimedes (n. 250 eaa) käytti piin arvon määrittämiseen 96-kulmaista säännöllistä monikulmiota ja todisti ensimmäisenä ympyrän ulko- ja sisäpuolelle piirrettyjen säännöllisten monikulmioiden avulla, että piin likiarvo on välillä $223/71 < \pi < 22/7$. Voit itsekin laskea piin arvon antiikin Kreikan tapaan Excel-taulukkolaskentaohjelman avulla seuraavasti. Kuvasta 2 havaitaan, että $OC = OA = BC = r = 1$. Pythagoraan lauseella kolmiosta OCD saamme

$$OD=\sqrt{{OC}^2-\left(\frac{BC}{2}\right)^2} \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (3)$$

Lisäksi huomaamme, että $AD = 1 – OD$, jonka jälkeen voimme käyttää uudestaan Pythagoraan lausetta AC:n laskemiseen kolmiosta ACD.

$$AC=\sqrt{{AD}^2+\left(\frac{BC}{2}\right)^2} \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (4)$$

Aukaise seuraavaksi Excel-taulukkolaskentaohjelma ja kirjoita laskukaavat edellisen pohjalta seuraavasti:

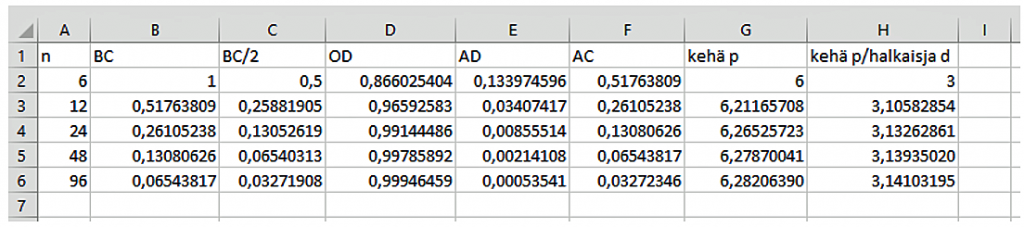
Kuvankaappaus excelistä. Piin laskemisen historiaa nykyaikaisesti. — Kuva 3: Excel -laskukaavat piin arvon määrittämiseksi Arkhimedeen menetelmällä.

Solussa G2 on laskettu koko kehän pituus kertomalla monikulmion sivun pituus niiden lukumäärällä. Koska ympyrän säteeksi on asetettu 1, niin ympyrän halkaisija on koko ajan 2 ja piin arvo on laskettu solussa H2 jakamalla monikulmion kehän pituus halkaisijalla eli kahdella, jolloin piin arvoksi kuusikulmiolla saadaan tasan kolme. Laitamme seuraavaksi soluun A3 kaavan, joka muuttaa kuusikulmion 12-kulmioksi kertomalla yläpuolella olevan solun kahdella. Tällöin 12-kulmiossa BC mitta on sama kuin AC:n mitta edellisellä rivillä ja soluun B3 on kirjoitettava kaava = F2. Nyt olet kirjoittanut kaikki Excel-kaavat, niin voit täyttökahvalla vetämällä kopioida laskukaavat riveittäin alaspäin ja voit laskea 6, 12, 24, … monikulmion avulla piin arvon. Arvo tarkkenee, kun monikulmioon tulee kulmia lisää. Kuvassa 4 on laskettu 6, 12, 24, 48 ja 96 monikulmiolle piin arvot.

kuvankaappaus excelistä — Kuva 4: Arkhimedeen laskut piin arvon määrittämiseksi on suoritettu Excel-taulukkolaskentaohjelman avulla.

Monikulmion jakaminen yhä pienempiin osiin oli piin laskemisessa muotia lähes seuraavat 2000 vuotta. Esimerkiksi saksalainen matemaatikko Ludolph van Ceulen laski 1500-luvun lopulla monikulmion, jossa oli 2⁶² sivua, avulla piin arvoa 25 vuotta ja sai piin arvon määriteltyä 35 desimaalin tarkkuudella. Nämä 35 piin desimaalia koristavat hänen hautakiveään vielä tänäkin päivänä.

Piin laskeminen äärettömän sarjan avulla

Vuonna 1665 englantilainen matemaatikko ja fyysikko Isaac Newton laski piin arvon äärettömän sarjan avulla aina 15 desimaaliin asti ollessaan karanteenissa Englannissa riehuneen ruton takia. Tämä mullisti piin laskemisen täysin. Newtonin sarjakehitelmä on muotoa.

$$\pi=\frac{3\cdot \sqrt3}{4}+24(\frac{2}{3\cdot 2^3}-\frac{1}{5\cdot 2^5}-\frac{1}{28\cdot 2^7}-\frac{1}{72\cdot 2^9}-\frac{5}{704\cdot 2^{11}}-\ldots)(5)$$

Pian tämän jälkeen myös skottilainen matemaatikko James Gregory kehitti piin laskemiselle äärettömän sarjan samanaikaisesti saksalaisen matemaatikon Gottfried Wilhelm Leibnizin kanssa. Gregoryn-Leibnizin ääretön sarja on muotoa

$$\frac{\pi}{4}=1-\frac{1}{3}+\frac{1}{5}-\frac{1}{7}+\ldots \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (6)$$

joka on itse asiassa sama kuin Intiassa hieman aikaisemmin keksitty ääretön sarja. Myös muita äärettömiä sarjoja kehitettiin piin laskemiseen. Äärettömät sarjat nopeuttivat piin laskemista ja niinpä vuonna 1699 saatiin jo laskettua 71 desimaalia piin arvolle. Piin likiarvon laskemiseen ei enää mennyt vuosia, vaan päiviä.

Myös kaavan 6 mukainen lasku on helppo tehdä Excelin avulla seuraavasti.

Kun kopioit lukuja ja laskukaavoja alaspäin täyttökahvan avulla alaspäin Excelissä, niin sekä solut A2 ja A3, että solut C2 ja C3 pitää kopioida täyttökahvalla pareittain alaspäin, jotta kaavat kopioituvat oikein. Huomaat nopeasti, että sarja suppenee todella hitaasti lähestyen piin arvoa.

Koska kreikan kielen sana περιφέρεια tarkoittaa ympyrän reuna-aluetta eli kehää, niin tästä inspiroituneena Welshiläinen matemaatikko Willam Jones otti vuonna 1706 ensimmäisenä käyttöön π-merkinnän omissa kirjallisissa julkaisuissaan. Merkintä on looginen, koska matemaattisissa julkaisuissa käytettiin ja käytetään kreikkalaisia kirjaimia. Merkintä vakiintui yleiseen käyttöön, kun myös aikansa tunnetuin matemaatikko Euler alkoi käyttää piin merkintää vuodesta 1727 alkaen myös omissa julkaisuissaan. Myös Euler kehitti oman äärettömän sarjan piin laskemiseksi.

Piin laskeminen tietokoneella

Vuonna 1949 piin desimaalien laskeminen nopeutui huomattavasti, kun piin laskemiseen käytettiin ensimmäisen kerran tietokonetta. Tällöin tykkien ampumaratojen laskemiseen kehitetty ENIAC-tietokone laski piin arvoa 70 tuntia ja sai tulokseksi 2037 desimaalia.

Matemaatikoille riittää piistä vallan hyvin 42 desimaalia, koska silloin saadaan kaikki laskut suoritettua jo protonin halkaisijan tarkkuudella, mutta siitä huolimatta piin likiarvojen laskemisesta on tullut suosittua huvia tietokoneiden kanssa, ja sitä käytetään usein vertailuarvona tietokoneiden käsittelytehon laskemisessa. Lisäksi tietokoneella laskettuja piin desimaaleja käytetään satunnaislukuina.

Vuonna 2019 japanilainen Emma Haruka Iwao, joka on Googlen työntekijä, laski 31 biljoonaa (3,1∙10¹³) desimaalia piille hyödyntäen Googlen pilvipalvelujärjestelmää. Uteliaisuus piin laskemiseen oli syttynyt Emmassa jo lapsuudessa. Tosin ennätyksen rikkoi jo seuraavana vuonna 2020 Timothy Mullican, joka sai 50 biljoonaa desimaalia piille. Mullican laski piin arvoa 303 päivää omalla tietokoneellansa. Mutta vuonna 2021 ennätys rikottiin uudestaan, jolloin Sveitsin Grisons-ammattikorkeakoulun supertietokone laski 108 päivässä 62,8 biljoonaa desimaalia piille. Tämä on Guinnesin ennätys tällä hetkellä. Laskemiseen tarvittiin 316 teratavua RAM-muistia. Periaatteessa tällaista tietokonetta ei ole olemassakaan, vaan tietokone käyttää laskemiseen tietokoneen kiintolevyjä.

Vuonna 1998 San Fransiscolainen Larry Shaw keksi viettää työkavereiden kanssa tiedekeskuksesaan piin päivää, jossa syötiin piirakoita ja pizzaa. Seuraavana vuonna juhlintaa laajennettiin pitämällä paraati, ja päivä alkoi saada julkisuutta. Juhlasta tuli niin suosittu, että se lopulta tunnustettiin kansalliseksi juhlapäiväksi vuonna 2009 ja sitä on alettu juhlia myös kansainvälisesti. Vuosi 2015 oli vuosisadan pii- päivä, koska päiväys voitiin kirjoittaa 3/14/15, kuten Amerikassa on tapana. Tänään piin päivänä voit sinäkin juhlia piitä monella tapaa.