Solmuja ja kilpikonnia

Keväällä 2022 opettajan pedagogisten opintojen Opettaja työnsä tutkijana -kurssillani suunniteltiin kaksi tieteelliseen tutkimukseen perustuvaa pedagogista tuotetta, jotka soveltuvat mainiosti matematiikan opetukseen. Materiaalit löytyvät MAOLin materiaalipankista. 

Atte Lohvansuun Solmuteorian mahdollisuudet koulumatematiikassa -tutkielmasta tarjolla ovat: opettajan itseopiskelumateriaali, joka sopii myös syventävää materiaalia kaipaaville lukiolaisille vapaaseen itseopiskeluun, yläkoululaisille suunnitellut aiheeseen johdattelevat opettajan diat ja oppitunnille tarkoitetut harjoitustehtävät ratkaisuineen. Tehtävät soveltuvat erinomaisesti myös jonkin lukion oppitunnin aiheeksi. Solmuteoria kytkeytyy vahvasti avaruusgeometriaan, mutta siitä löytyy aineksia myös matemaattisen todistamisen harjoitteluun, joten toivottavasti ne löytävät paikkansa opetuksessa ja tuottavat opiskelijoille ja oppilaille iloa.

Heini Auvisen ja Milla Höglundin tutkielma Ohjelmointi & Geometria – Python-kilpikonnagrafiikka-ajokortti geometrisen ajattelun ja ymmärryksen tukena sisältää 7. luokan oppilaille suunnitellun tehtäväpaketin, opettajan tukipaketin, jossa tehtäviin on myös ratkaisut, ja Kilpikonna-ajokortin. Ajokortin tavoitteena on jäsentää oppilaiden työskentelyä ja tuoda siihen samalla hiukkasen pelillisyyttä. Materiaali yhdistää hauskasti geometrian peruskäsitteiden opiskelun ja Python-ohjelmoinnin harjoittelun toisiinsa. Seuraavaksi esittelen tarkemmin molempia materiaaleja lainaten paloja tutkielmista.

Solmuja

Solmuteoria on nimensä mukaisesti solmuja tutkiva matematiikan osa-alue. Tarkemmin sanottuna kyse on topologian osa-alueesta, mutta järeää matematiikkaa tarvitaan oikeastaan vain, jotta solmu saadaan matemaattisena käsitteenä tarkasti määriteltyä. Itse teorian alkeet ovat varsin konkreettisia ja yllättävän hyvin maalaisjärjellä selitettävissä.

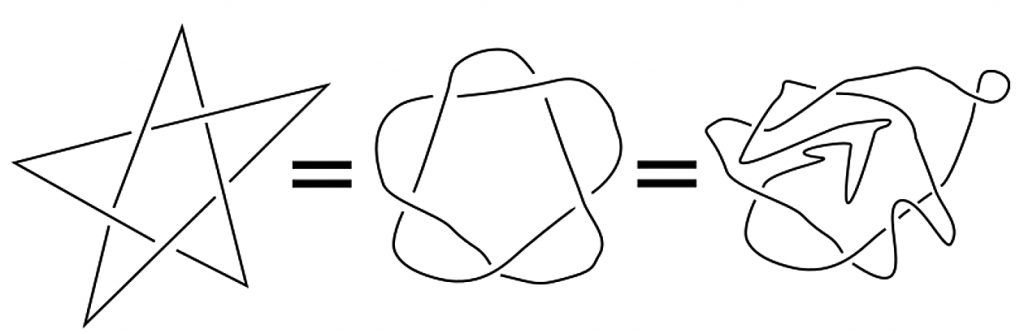
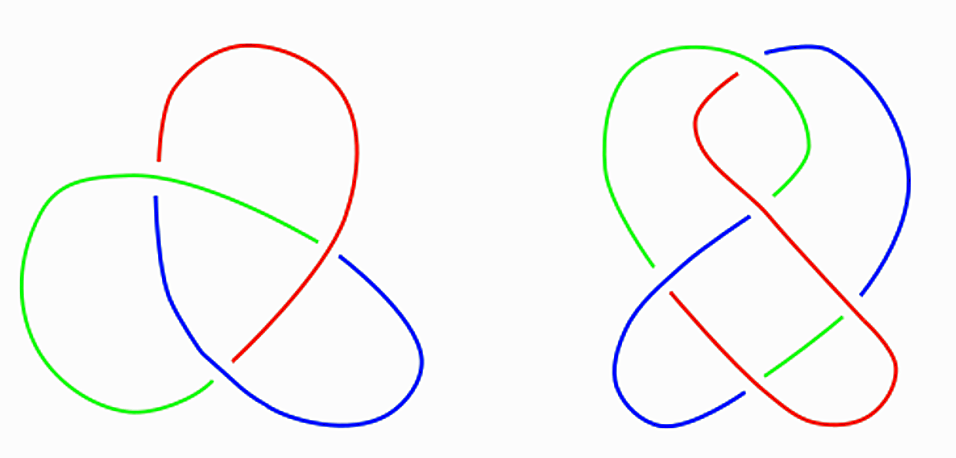
Matemaattinen solmu on yksinkertainen kolmiulotteisen avaruuden silmukka. Yksinkertaisuudella tarkoitetaan, ettei silmukka leikkaa itseään missään pisteessä. Kuvassa 1 on esitelty kolme solmua, jotka ovat samoja solmuja eli ekvivalentteja keskenään. Solmujen kolmiulotteisuus tuodaan esiin jättämällä alle jäävistä silmukan osista pieni pätkä piirtämättä. Solmuteorian kaksi perimmäistä kysymystä ovat: minkälaiset solmut ovat triviaaleja eli eivät solmuja lainkaan, vaan pelkkiä ympyröitä? Entä minkälaiset solmut ovat ekvivalentteja eli ne saadaan joillakin siirroilla toinen toisistaan? Näitä kysymyksiä voidaan tutkia kolmivärityksillä kuten kuvassa 2, jossa ns. apilasolmu havaitaan aukeamattomaksi. 

Solmuteorian raportoiduista opetuskokeiluista suurin osa on tehty Japanissa. Lohvansuu jakaa löytämänsä kokeilut neljään kategoriaan: 

1. Mallien ymmärtäminen Näissä kokeiluissa keskitytään solmujen kaksi- ja kolmiulotteisten mallien havainnoimiseen, rakentamiseen, piirtämiseen ja muokkaamiseen.
2. Apila ei ole triviaali Kokeiluissa tavoitteena on todistaa apilasolmun aukeamattomuus tyypillisesti kolmiväritysten avulla.
3. Peilikuvat ja polynomit Kokeiluissa tavoitteena on todistaa apilasolmun eroaminen peilikuvastaan.
4. Muut kokeilut.

Mallien ymmärtämisen tavoitteena on kehittää oppilaiden avaruudellista hahmotuskykyä, ja tehtävät liittyvätkin kokeiluissa aluksi konkreettisen solmun tekemiseen kuvasta (2D -> 3D) ja toiseen suuntaan eli kuvan piirtämiseen itse tehdyistä solmuista (3D -> 2D). Fyysisten solmujen pyörittelyn ja diagrammien piirtelyn jälkeen on luonnollista kysyä, onko triviaaleja solmuja olemassa, aukeavatko kaikki solmut, ja jos näin on, miten voisimme sen todistaa. Yksinkertaisin epätriviaali solmu on apila, ja sen jokainen osaa varmasti solmia. Helpoin tapa todistaa apilan epätriviaalius on kolmivärittäminen. Toisen kategorian kokeilut liittyvätkin värittämistehtäviin. Kolmivärittämiset eivät välttämättä tunnu kovin matemaattisilta, ainakaan lukiolaisista, sillä kolmiväritettävyys jakaa kaikki solmut vain kahteen kategoriaan: ne, jotka ovat kolmiväritettäviä ja ne, jotka eivät ole. Tämän tiedon avulla ei siis voi erottaa kolmea solmua toisistaan. Tähän ongelmaan itseopiskelumateriaali tarjoaa lisää välineitä ja kolmannen kategorian tehtävät liittyvätkin juuri peilikuviin ja niin sanottuihin polynomeihin. Japanissa tehtyjen opetuskokeilujen perusteella lukiolaiset kokivat aiheen haastavana, mutta opettajan mielestä solmuteoria oli matemaattisen ajattelun kannalta hyödyllistä erityisesti siksi, että opiskelijat voivat pohtia ja myös osata solmuteoriaa olematta erityisen päteviä laskijoita.

Solmuteorian alkeiden oppiminen voi siis tuoda yläkoulun oppitunneille kaivattua konkretiaa ja toiminnallisuutta, kehittää oppilaiden avaruudellista hahmotuskykyä ja erityisesti lukiolaisille antaa mahdollisuuksia tutustua avaruusgeometrian yhteydessä ylipäätään melko vähiin jäävään matemaattiseen todistamiseen. Lopuksi vielä maistiaisia itse tehtäväpaketista.

Kilpikonnia

Python kilpikonna-grafiikkaohjelmointiin liittyvät tehtävät on suunniteltu yläkouluun, ja ne perustuvat van Hielen geometrisen ajattelun kehittymisen teoriaan. van Hielen teoriassa on kyse viidestä tasosta, joilla oppilaan geometrisen ajattelun on havaittu kehittyvän. Ensimmäinen tasoista on visualisoinnin taso eli tunnistamisen taso. Tällä tasolla oppilas tunnistaa erilaisia geometrisia kuvioita kuten kolmion, neliön ja ympyrän. Toinen taso on ominaisuuksien analysoinnin taso ja silloin oppilas tietää jo kuvioiden ominaisuuksia esimerkiksi sen, että kolmiolla on kolme kulmaa. Kolmannella tasolla ominaisuuksien järjestämisen tasolla oppilas tietää riittävät kuvioiden ominaisuudet esimerkiksi sen, että kolmion sivut ovat janoja ja kolmion kulmien summa on 180 astetta. Neljännellä, formaalin päättelyn tasolla, oppilas pystyy todistamaan kolmion eri ominaisuuksia ja korkeimmalla viidennellä tasolla, aksiomisysteemin ymmärtämisen tasolla, oppilas pystyy vertailemaan eri geometrioita keskenään tarkastelemalla niiden eroja ja yhtäläisyyksiä. Laadittu tehtäväpaketti huomioi erityisesti van Hielen teorian ominaisuuksien analysoinnin ja ominaisuuksien järjestämisen tasot. 

Ohjelmointi tuo Auvisen ja Höglundin mielestä mielekkään lisän geometrisen ajattelun kehittämiseen. Mielekkään oppimisen keskiössä on ymmärtäminen, ja sen piirteitä ovat konkreettisuus, kontekstuaalisuus ja sosiaalisuus. Ohjelmoitaessa mielekkyys korostuu, koska oppilas voi reaaliajassa nähdä työnsä tuloksia. Lisäksi tietokoneella ohjelmointi vaatii tarkkaa algoritmista ymmärrystä ohjelmoitavasta asiasta. Geometria on puolestaan mielekäs matematiikan osa-alue juuri visualisuutensa ja konkreettisuutensa vuoksi. Geometrisen kuvion kuvailu on kuin antaisi kappaleelle sopivan algoritmin. Auvinen ja Höglund kertovat tutkielmassaan Foersterin (2016) tutkimuksesta, jossa osa oppilaista sai aluksi ohjelmoida geometrisia kuvioita, kun taas osa oppilaista ei ohjelmoinut lainkaan. Tutkimuksessa ilmeni, että ohjelmoineet oppilaat pystyivät antamaan ytimekkäämpiä selityksiä geometrisille kuvioille kuin ne oppilaat, jotka eivät ohjelmoineet. Myös Heirm ja Johnsen-Høines (2021) tutkivat ohjelmoinnin vaikutusta geometristen kuvioiden oppimiseen. Tutkimuksessa seurattiin kahden 7. luokkalaisen oppilaan prosessia, kun tavoitteena oli ohjelmoida Scratch-ohjelmointikielellä viisikulmio. Tuloksina havaittiin, että ohjelmoimalla aikaan saadut kuviot antoivat oppilaille heti palautetta koodin sujuvuudesta ja ohjelmoidessaan oppilaat pääsevät itse toteuttamaan tutkivaa oppimista. Lisäksi ohjelmoitaessa tehdyt valinnat ja prosessin ymmärtäminen ovat ratkaisua kohti edettäessä yhtä tärkeitä kuin lopulta itse ratkaisu.

Laaditussa opiskelumateriaalissa on kuusi ohjelmointitehtävää ja niiden tukena on ohjeita ohjelmoinnin aloitukseen, kilpikonnan liikkumiseen ja kunkin tehtävän edellyttämiin lisäominaisuuksiin. Seuraavaksi yksi maistiaistehtävä.