Sykliset monikulmiot 1234…
Alkeisgeometriasta voidaan muotoilla piirtämistehtäviä, jotka näennäisestä yksinkertaisuudestaan huolimatta eivät aina ole ihan yksinkertaisia. Näitä ovat esimerkiksi sykliset monikulmiot, joiden sivut ovat kokonaislukuja 1, 2, 3, 4, …
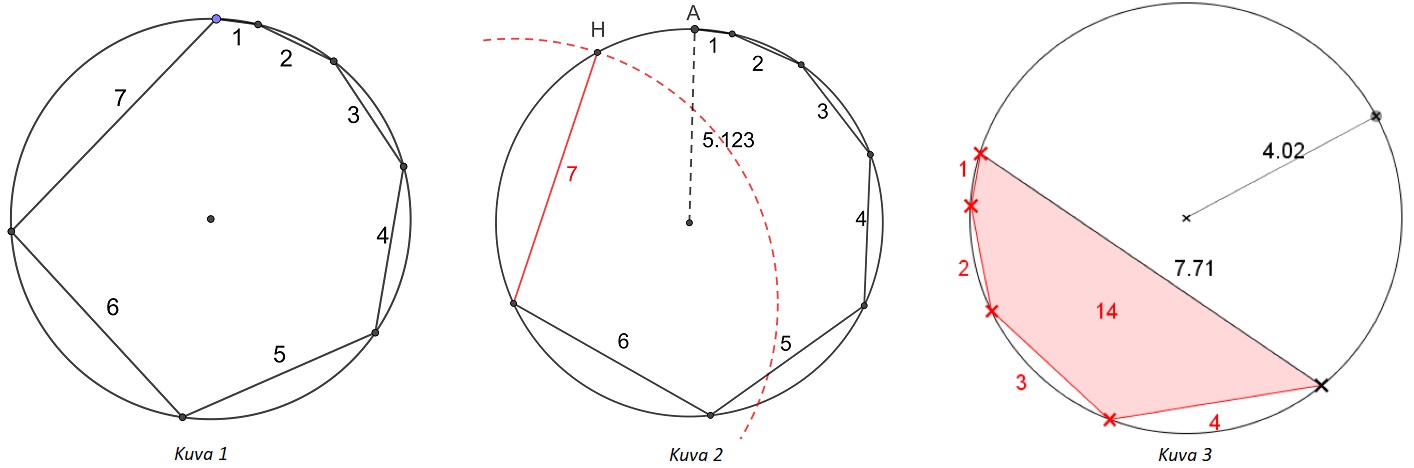
Monikulmio on syklinen, jos sen ympäri voidaan piirtää ympyrä. Syklisen monikulmion sivut ovat ympäri piirretyn ympyrän jänteitä, joten sitä voidaan kutsua myös jännemonikulmioksi. Idea on helppo hahmottaa esimerkiksi seitsenkulmiosta (Kuva 1). Likiarvoratkaisu saadaan dynaamisesta kuvasta, jossa ympyrän säde on säädettävissä. Piirretään (tarpeeksi iso) ympyrä, ja siihen peräkkäin haluttu määrä jänteitä (Kuva 2). Kun sädettä pienennetään, niin pisteet H ja A asettuvat päällekkäin. Siitä saadaan säteen likiarvo.
Samantapaisia jännemonikulmioita tarkasteltiin Dimension 2/2013 pulmasivulla [1]. Sen ratkaisut ovat kadonneet MAOLin verkkosivuilta monien uudistusten myötä, mutta Docplayer on ne säilyttänyt [2]. Silloin Simo Kivelä analysoi kuvion piirtämistä Mathematicalla. Tarkasteltavana oli yleisempi tapaus, jossa viimeisen sivun pituus sai vaihdella. Kysyttiin, mitä arvoja jännemonikulmion viimeinen sivu ja pinta-ala voivat saada sivujen lukumäärän eri arvoilla säteen vaihtuessa (Kuva 3).
Mallikuvaksi Kuva 1 jo kelpaa. Entä tarkempi ratkaisu? Kun monikulmion kaikki sivut 1, 2, 3, …, n on annettu, niin ongelmana on vain ympyrän säteen määritys. Laskemista on pidetty ongelmallisena, sillä siitä on sanottu muun muassa näin [3]: ”Syklisen monikulmion ulkoympyrän säde – – voidaan laskea vain erityisissä tapauksissa sivujen tai lävistäjien pituuksien avulla.” Tietokonealgebrasysteemi tarjoaa kuitenkin helposti käsiteltävän yleisen ratkaisun.
Jänteitä vastaavat keskuskulmat täyttävät koko ympyrän. Säteen pituus r saadaan siis kullakin pisimmän sivun n arvolla yhtälöstä
$\sum_{i=1}^n\arcsin\left(\frac{i}{2r}\right)=180°{,}\ n>3.$
Yhtälö ei ratkea ihan helposti, sillä esimerkiksi tapauksessa n = 7 Geogebra-CAS keskeyttää suorituksen ja sanoo, että ratkaiseminen kestää liian kauan. Numeerinen ratkaisu r ≈ 4,4753725744 sen sijaan tulee vilauksessa, myös isommille n:n arvoille. Huomaa, että n:n arvolla 3 ei muodostu monikulmiota.
Tapauksessa n = 4 säde voidaan laskea Brahmaguptan kaavaan perustuvalla kaavalla [4]:
$r_4=\frac{\sqrt{\frac{385}{6}}}{4}\approx2{,}00260247345.$
Suuremmilla n:n arvoilla sädettä ei voida ilmoittaa juurten avulla. Mathematica käyttää tällöin Root-funktiota. Esimerkiksi tapauksissa n = 5 tai n = 6 tarvitaan Kivelän mukaan astetta 14 olevan polynomiyhtälön ratkaisua. Harpilla ja viivaimella kuvioita ei voi siis piirtää. Syklisiä monikulmioita ei voida yleensäkään piirtää annetuista sivuista lähtien, kun n ≥ 5 [5]. Ei siis ihme, että Geogebra ei suostunut tarkkaa arvoa laskemaan tapauksessa n = 7.
Oikean muotoinen kuvio voidaan piirtää mielivaltaisella tarkkuudella käyttäen hyväksi ympäri piirrettyä ympyrää, jonka säteen likiarvo voidaan laskea edellä esitetyllä tavalla, kun n > 3. Merkitään sitten ympyrän kehälle pisteet, joiden peräkkäiset etäisyydet ovat 1, 2, 3, …, n. Ja piirretään monikulmio nämä pisteet kärkipisteinä (mallikuvan 1 mukaisesti).
Kilpikonnagrafiikalla piirrettäessä ympyrääkään ei tarvita, kun tietää, kuinka paljon on käännyttävä kunkin sivun piirtämisen jälkeen (Kuva 4). Oikokulmasta vähennetään kärjessä kohtaavien keskuskolmioiden kantakulmat
180o – arccos(n / (2 r)) – arccos((n + 1) / (2 r)).
Käytin piirtämiseen FMSLogoa (kuva 5). Myös Geogebran kilpikonnageometrialla se onnistuu, vaikka sen skriptieditori onkin hyvin kankea ja yksioikoinen eikä siinä ole mitään kirjoittamista helpottavia tekstinkäsittelytoimintoja.
Yleisesti voidaan todistaa, että on olemassa syklinen monikulmio, jonka sivut ovat a1, a2, …, an, jos jokainen sivuista on pienempi kuin muiden sivujen summa, ja että kuvio on yksikäsitteinen.
Lisää luettavaa
[1] Pulmasivu. Dimensio 2/2013.
[2] Dimension 2/2013 pulmasivun ratkaisuja osoitteessa https://docplayer.fi/30777816-Korhonen-s-problem-ratkaisuja-hannu-korhonen.html
[3] Wikipedia-artikkeli Syklinen monikulmio osoitteessa https://fi.wikipedia.org/wiki/Syklinen_monikulmio.
[4] Moritsugu, Shuichi: Computation and Analysis of Explicit Formulae for the Circumradius of Cyclic Polygons. Communications of JSSAC (2018), Vol. 3, pp. 1–17. Osoitteessa http://www.jssac.net/Editor/CJssac/V03/V3_101.pdf
[5] Czédli, Gábor ja Kunos, Ádám: Geometric constructibility of cyclic polygons and a limit theorem. University of Szeged, Bolyai Institute. Szeged, Hungary, 2015. Osoitteessa http://www.math.u-szeged.hu/~czedli/publ.pdf/czedli-kunos_geometric-constructibility-of-cyclic-polygons-and-a-limit-theorem.pdf







