Tekoäly matematiikan kokeissa
Lempäälän lukiossa tutkittiin helmikuussa 2025 tekoälyn kykyä suoriutua erilaisista matematiikan kokeista. Ohjelmalle syötettiin kokeen tehtävänanto kuvakaappauksena, minkä jälkeen tarkasteltiin ohjelman antamaa vastausta. Kokeiksi valittiin valtakunnallisista kokeista matematiikkakilpailun loppukilpailu sekä MFKA-kustannuksen kevään 2025 pitkän matematiikan preliminäärikoe.
Tekoäly matematiikkakilpailun loppukilpailussa
Aluksi tutkittiin tekoälyn kykyä ratkaista Matemaattisten aineiden opettajien liiton (myöhemmin MAOL) matematiikkakilpailun tehtäviä. MAOL järjestää matematiikkakilpailuja erikseen peruskouluun ja lukioon. Lukion kilpailussa on kolme sarjaa iän mukaan: avoin, väli- ja perussarja, joista avoin sarja on vaikein. Kunkin sarjan parhaat pääsevät loppukilpailuun. Tutkimuksessa tutkittiin lukion matematiikkakilpailun loppukilpailukysymyksiä.
Verkossa oli saatavilla vanhoja loppukilpailutehtäviä vuoteen 2019 saakka sekä vuoden 2025 loppukilpailu. Jokaisessa kokeessa oli viisi avointa tehtävää, jotka piti ratkaista. Tutkimuksessa rajattiin pois matematiikan todistustehtävät eli tehtävät, joiden tehtävänanto alkaa esimerkiksi sanoilla ”Osoita, että” tai ”Todista väite”. Toisin sanoen loppukilpailutehtävistä huomioitiin vain ne, joiden vastaus on esimerkiksi luku, lauseke tai funktio.
Alussa vertailtiin ChatGPT:n (versio 4o), Google Geminin (versio 2.0 flash) ja Deepseekin antamia vastauksia. Tehtävä katsottiin ratkaistuksi oikein, jos ohjelma oli päätynyt oikeaan lopputulokseen. Tutkimuksessa ratkaisu olisi joko oikein tai väärin. Välivaiheiden oikeellisuutta ei siis tarkasteltu.
Oheisessa taulukossa on kuvattu ohjelmistojen oikeat ja väärät vastaukset. Merkintä 1 tarkoittaa oikean vastauksen saamista (merkitty vihreällä), merkintä 0 tarkoittaa väärää vastausta. DeepSeekin merkintä ”-” tarkoittaa ohjelmiston toiminnan keskeytymistä.
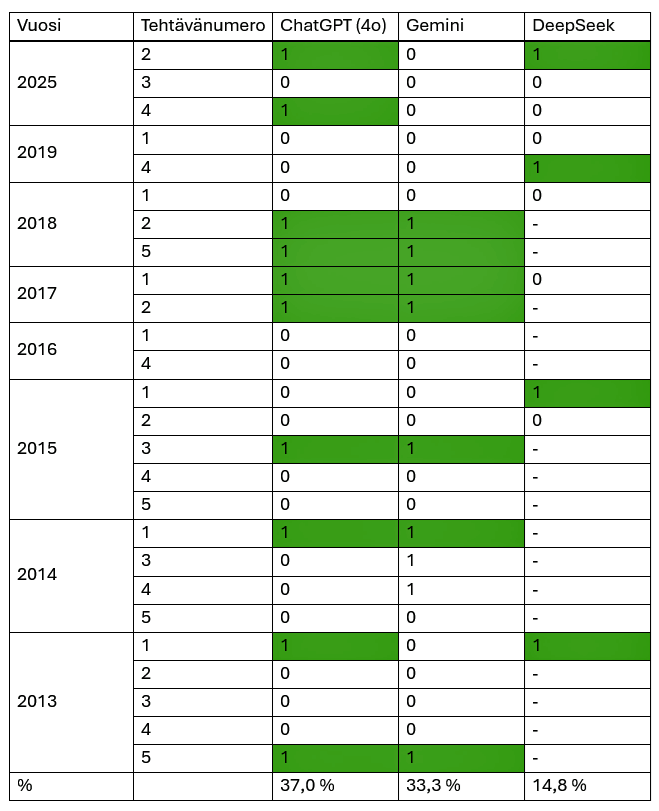
Tutkimuksen jälkeen perehdyttiin ChatGPT:n kehittyneempiin kielimalleihin. Oheisessa taulukossa on kielimallien julkaisuajankohdat.
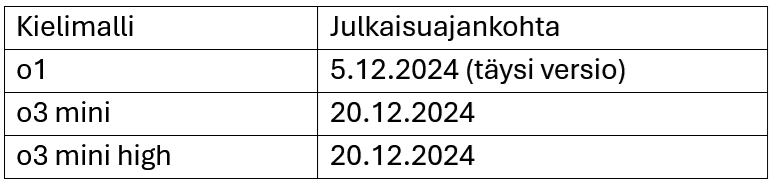
OpenAI:n kielimallit o1, o3 mini ja o3 mini high eroavat toisistaan laskentatehon, tarkkuuden ja vasteajan suhteen. Kielimalli o1 on suunniteltu monimutkaisiin tehtäviin, kuten matematiikkaan ja koodaukseen, mutta sen vasteaika on hitaampi. Kielimalli o3 mini on nopeampi ja kustannustehokkaampi kuin o1, ja se tarjoaa hyvän suorituskyvyn tavallisissa tehtävissä. o3 mini high on tarkempi ja parempi monimutkaisissa ongelmissa, mutta se on hitaampi kuin o3 mini ja saatavilla vain maksullisille käyttäjille.
Seuraavaksi tutkittiin näiden kielimallien kykyä ratkaista ne tehtävät, joita ChatGPT:n aiempi kielimalli 4o ei kyennyt ratkaisemaan. Tutkimuksessa rajoituttiin nyt siis ratkaisematta jääneisiin tehtäviin. Oheisessa taulukossa on kuvattu kehittyneempien kielimallien kyky suoriutua näistä tehtävistä.
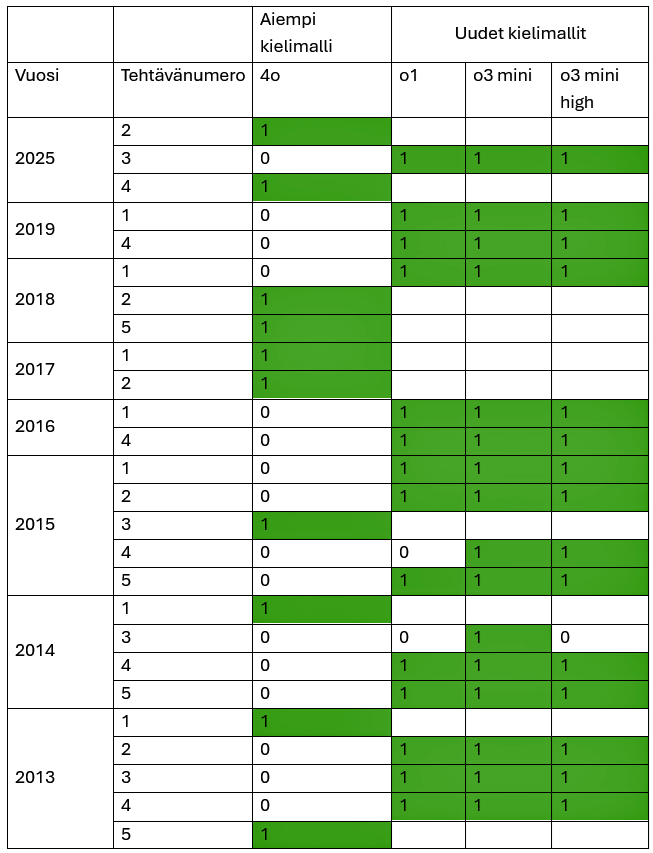
Tuloksista havaitaan, että ChatGPT:n kielimalli o3 mini kykeni ratkaisemaan oikein kaikki tehtävät ja kaksi muuta kielimallia kykenivät lähes vastaavaan.
Tekoäly preliminäärikokeessa
Seuraavaksi tutkittiin tekoälyn kykyä ratkaista MFKA-Kustannuksen laatiman kevään 2025 pitkän matematiikan preliminäärikokeen tehtäviä. Rakenteeltaan koe mukaili matematiikan ylioppilaskoetta. Kokeen rakennetta on kuvattu oheisessa taulukossa. Kaikki kokeen tehtävät ovat 6 pisteen tehtäviä.
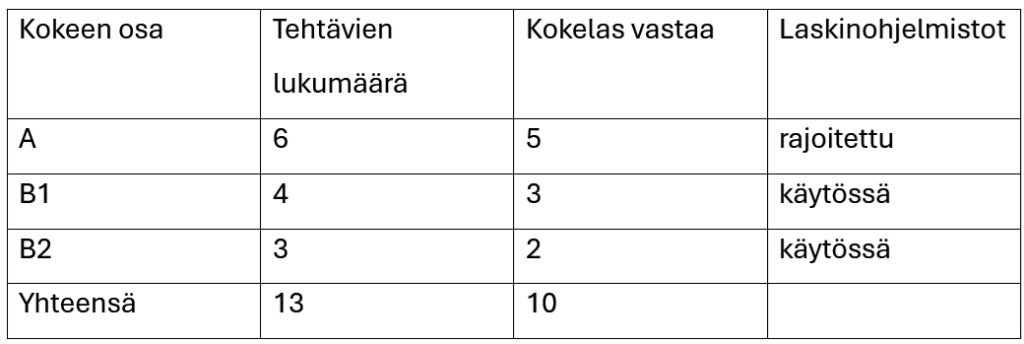
Tutkimuksen alussa vertailtiin ChatGPT:n (versio 4o) ja Google Geminin (versio 2.0 flash) antamia vastauksia. DeepSeek jätettiin pois tutkimuksista ohjelman jatkuvan keskeytymisen vuoksi. Lopuksi tutkittiin uudelleen tehtäviä, joita kielimalli 4o ei kyennyt ratkaisemaan täysin oikein. Nämä tehtävät ratkaistiin vielä ChatGPT:n kehittyneemmillä kielimalleilla o1, o3 mini ja o3 mini high. Tehtävät pisteytettiin MFKA-Kustannuksen ohjeiden mukaisesti. Tulokset on esitetty oheisessa taulukossa.
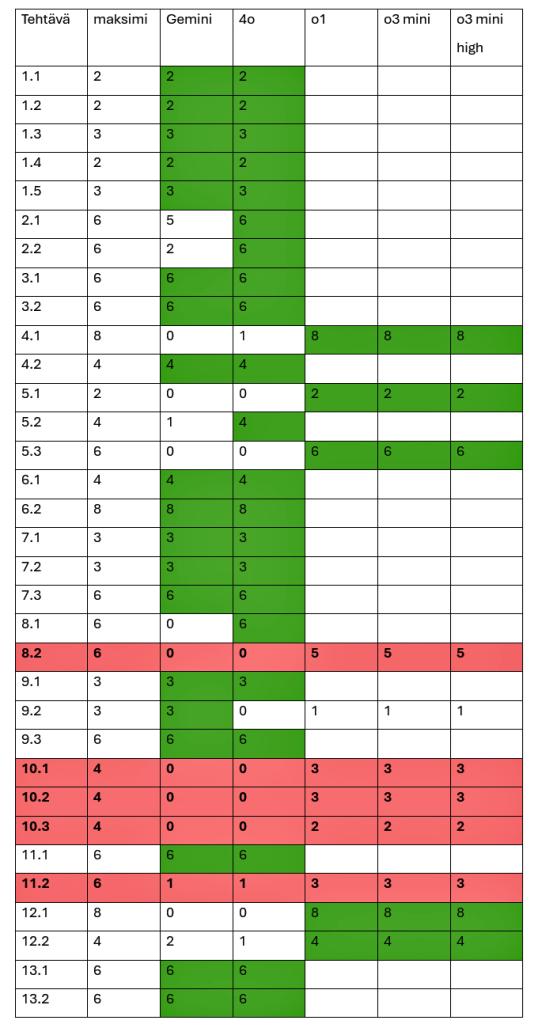
Tuloksista havaitaan, että kehittyneimmät kielimallit kykenivät ratkaisemaan lähes kaikki preliminäärikokeen tehtävät. Maksipistemäärää mikään kehittynein kielimallia ei kyennyt saavuttamaan viidessä osatehtävässä (8.2, 10.1, 10.2, 10.3 ja 11.2).
Aidossa koetilanteessa opiskelijat saivat valita osioista A, B1 sekä B2 määrätyn lukumäärän verran tehtäviä ja vastata niihin. Tutkimuksessa puolestaan ratkaistiin kaikki tehtävät. Tekoälyn saamaa pistemäärää voi hahmottaa jakamalla kunkin osion kokonaispistemäärä tehtävien lukumäärällä ja kertomalla saatu osamäärä luvulla, joka vastaa vastattavien tehtävien lukumäärää. Näin laskemalla tekoälyn avulla saavutettiin noin 110,4 pisteen suoritus. Pistemäärä vastaa Lempäälän lukiossa tehdyn kokeen (n=76) toisiksi parasta pistemäärää. Kokeessa parhaiten suoriutuneen opiskelijan pistemäärä oli 114 pistettä, kokeen keskiarvo 43,3 pistettä ja keskihajonta 25,9 pistettä.
Lopputuloksena voidaan todeta, että kehittyneimmät kielimallit suoriutuivat preliminäärikokeesta erinomaisesti ja muutkin kielimallit hyvin. Kehittyneimpien kielimallien suurimmat ongelmat olivat talousmatematiikan desimaalien käsittelyssä (tehtävä 8) ja oikean päivämäärän selvittämisessä annetun ohjeen mukaan (tehtävä 10). Osatehtävässä 11.2 tekoälyohjelmat yrittivät monin keinoin saada annetun funktion käänteisfunktiota selville, vaikka tehtävä olisi helpommin ratkaistavissa symmetrian avulla. Käänteisfunktion selvittäminen ei ohjelmilta onnistunut ja ratkaisu jäi kesken.







