Matemaattisia taikoja ja variaatioita muistilehtiöstäni, osa 4: Taikuriparaati The Linking Ring -lehdessä
The Linking Ring on maailmanlaajuisen taikuriyhdistyksen The International Brotherhood of Magicians (I.B.M.) jäsenlehti. Yhdistys perustettiin vuonna 1922 ja ensimmäiset The Linking Ring -lehdet ilmestyivät jo samaisena vuonna. Tänään lehti leviää kahdeksankymmeneenkahdeksaan maahan ja yli kahdellekymmenelletuhannelle yhdistyksen jäsenelle.
Taikatemput ovat aina olleet tärkeä osa taikurilehtiä. 1950-luvulla The Linking Ring alkoi julkaisemaan Hocus Pocus Parade -nimistä sarjaa. Yhteen paraatiin koottiin lehden lukijoiden lähettämiä taikatemppuja. Myöhemmin idea kehittyi niin, että yhden lehden tempuista, temppuparaatista, vastasi yksi taikuri. Palstan nimikin on One-Man-Parade.

Olen lähettänyt kaksi kertaa temppujani The Linking Ring -lehteen, ja molemmilla kerroilla ne on myös julkaistu One-Man-Parade -palstalla. Ensimmäinen ilmestyi maaliskuussa 2015. Tuolloin kerroin lehden lukijoille yhdeksän sivun ja kuuden tempun avulla, että näkövammaisille, jopa sokeille voidaan esittää taikatemppuja. Kyllä, minä teen paljon muutakin kuin matemaattisia taikatemppuja. Viime vuoden maaliskuussa The Linking Ring -lehdessä julkaistiin paraatini matemaattisista taikatempuistani, yksitoista temppua ja kaksitoista sivua taikuutta. Samalla pääsin lehden kansikuvapojaksi, noin kahdeksan vuotta vanhalla kuvallani. Koska lehteä ei saa kuin olemalla I.B.M:n jäsen, laitan tähän temppuparaatissani olleen ideani sellaisenaan.
Yksi kahdeksasta
Katsoja valitsee yhden kortin kahdeksasta mahdollisesta. Sekoitusten jälkeen toinen katsoja löytää ensimmäisen katsojan valitseman pelikortin. Taikurikaan ei tiedä katsojan valintaa kuin vasta tempun lopussa.
Temppu

Taikuri antaa katsojalle kahdeksan pelikorttia ja pyytää katsojaa valitsemaan mielessään yhden korteista. Katsoja levittää kortit eteensä ja valitsee mielessään yhden korteista.
Kun katsoja on tehnyt valintansa, taikuri huomauttaa, että hän saattoi nähdä, mitä korttia katsoja tuijotti. Niinpä taikuri pyytää katsojaa sekoittamaan pakkaa.
Korttien sekoittaminen on kokemattomalle yleensä vaikeaa, ja yllättävästi pienellä pakalla sekoittaminen on vieläkin vaikeampaa.
Kun taikuri huomaa katsojan kamppailun pelikorttien kanssa, taikuri lupaa opettaa sekoittamistavan, joka sopii oikein hyvin pienelle korttimäärälle. Sekoitus on 1700-luvulta, ajalta, jolloin jo pelikorttien laatu vaati yksinkertaisen sekoitustavan.
Taikuri myöntää, että katsoja saattaa kuvitella, että häntä huijataan tässäkin asiassa. Niinpä taikuri pyytää katsojaa tarkistamaan, monentenako hänen valintansa on juuri nyt. Sekoituksen jälkeen on helppo todentaa, että katsojan kortti on mennyt muualle, joten todennäköisesti kaikki muutkin kortit ovat vaihtaneet paikkansa.
Katsoja tarkistaa kortin paikan ja pitää mielessään, monentenako hänen korttinsa pakassa on. Tätä tietoa ei kuitenkaan kerrota taikurille.
Seuraavaksi taikuri näyttää Monge-sekoituksen.
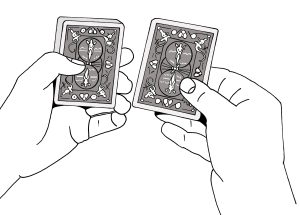
Kortit ovat vasemmassa kädessä ja ne siirretään yksitellen oikeaan käteen. Vasemman käden peukalo työntää pakan ensimmäisen kortin oikeaan käteen.

Seuraavaksi vasemman käden peukalo työntää pinon kakkoskortin oikeaan käteen. Se viedään oikeassa kädessä olevan kortin päälle.

Samalla tavalla vasemman käden peukalo työntää kolmannen kortin oikeaan käteen. Kolmas kortti viedään oikeassa kädessä olevien kahden kortin alle.
Vasemman käden peukalo työntää neljännen kortin oikeaan käteen ja tällä kertaa kädessä olevien kolmen kortin päälle.
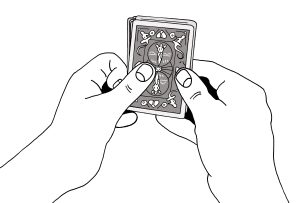
Tällä tavalla jatketaan siirtämällä kortteja vuorotellen oikeassa kädessä olevien korttien päälle ja alle. Kun kahdeksan korttia siirretään tällä tavalla yksitellen oikeaan käteen, viimeinen kortti tulee oikean käden pelikorttien päälle.
Taikuri toistaa sekoituksen vielä kaksi kertaa, jotka kortit varmasti menevät sekaisin. Kolmen Monge-sekoituksen jälkeen taikuri kysyy katsojalta, monentenako hänen korttinsa oli äsken, ennen Monge-sekoituksia. Katsoja kertoo kortin alkuperäisen sijainnin. Taikuri näyttää kortin, joka on tällä hetkellä tuossa kohtaa pakkaa. Huomataan, että se ei ole katsojan kortti. Kortit ovat siis oikeasti menneet sekaisin.
Seuraavaksi taikuri jakaa kortit pöydälle. Hän pyytää toista katsojaa avuksi, ja muutamien valintojen jälkeen päädytään tilanteeseen, jossa pöydällä on enää yksi kortti. Taikuri kysyy ensimmäiseltä katsojalta hänen valintaansa. Pöydälle jäänyt kortti osoittautuu olevan katsojan valinta.

Selityksiä
Mongesekoitus tehdään joka kerta samalla tavalla. Kortit siirtyvät vuorotellen vasemmasta kädestä oikeaan käteen ja menevät oikeassa kädessä vuorotellen korttien päälle ja alle. Tämä mahdollistaa sen, että voimme tutkia korttien etenemistä ja niiden järjestystä ennen sekoitusta ja sekoituksen jälkeen. (*
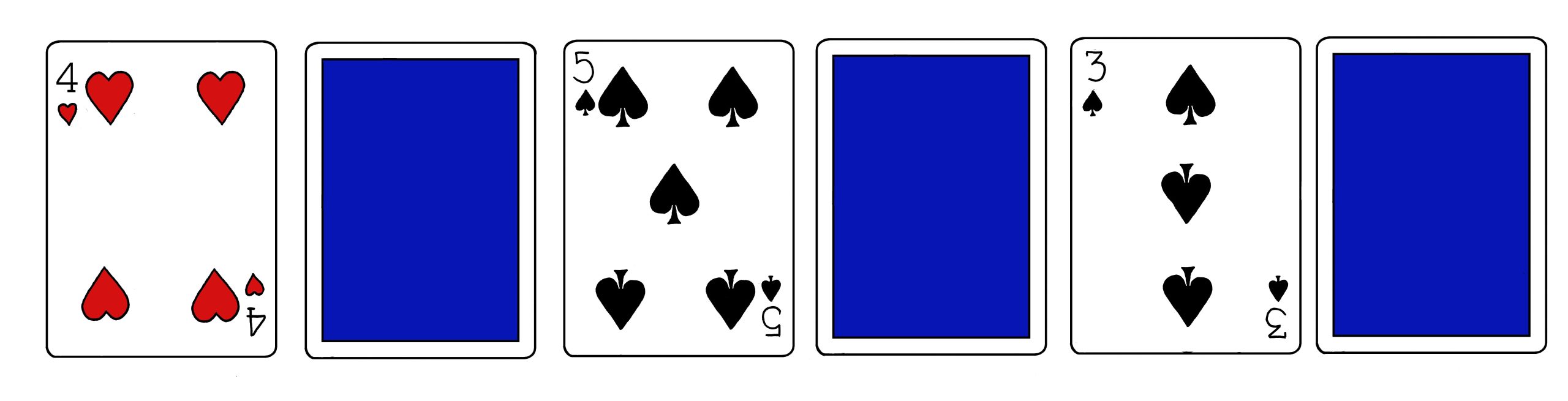
Jos korttien järjestys on 1, 2, 3 4, 5, 6 7, 8, on järjestys kolmen Monge-sekoituksen jälkeen 5, 4, 6, 3, 7, 2, 8, 1.
Korttien järjestys näkyy kuvassa sen jälkeen, kun kortit on jaettu pöydälle kahteen riviin.
Lukujono on helppo muistaa, kun ajattelet lukuja parittain: 5,4 6,3 7,2 8,1
Jokaisessa parissa ensimmäinen luku on aina yhtä suurempi kuin edellisen parin ensimmäinen luku. (5, 6, 7, 8,) Samalla tavalla jokaisessa parissa toinen luku on yhtä pienempi kuin edellisen parin toinen luku. (4, 3, 2, 1). Lisäksi parien summa on aina yhdeksän. No, muistisääntöjen määrällä ei ole merkitystä, kunhan sellainen sinulla vain on. Itselläni on tapa jopa laskea mielessä korttien järjestysluvut, kun jaan ne pöydälle. Sellainen helpottaa muistamista.
Sekoitusten jälkeen katsoja ilmoittaa valitun kortin alkuperäisen järjestysnumeron. Sinä näytät, että siinä kohtaa ei hänen valintaansa enää ole. Samassa jaat kortit pöydälle kahteen riviin. Koska tiedät, missä katsojan kortti on, tästä eteenpäin tempun voi lopettaa monellakin tavalla.
Minulla on tapana pyytää toista katsojaa avustajaksi ja edetä Taikurin valinta -tekniikalla.
Aivan ensimmäisenä kysyt katsojalta ylärivi vai alarivi? Samalla heilautat kättäsi kohti kortteja niin, että sanalla ylärivi näytät katsojan suunnalta alariviä ja sanalla alarivi heilautat kättäsi katsojan suunnalta katsottuna kohti yläriviä. Katsoja hämääntyy kysymyksestä ja onkin aivan sama mitä hän vastaa. Sinä toistat sen, mitä hän sanoo ja poistat sen rivin, jossa katsojan valitsema pelikortti ei ole. Pöydälle jää neljä korttia. Pyydä katsojaa siirtämään kaksi korttia sinuun päin. Jos näissä korteissa ei ole valittua pelikorttia, siirrä se sivuun. Jos toinen näistä korteista on katsojan valinta, pyydä katsojaa siirtämään riviin jääneet kaksi korttia pois. Kummassakin tapauksessa pöydälle jää kaksi pelikorttia. Pyydät katsojaa siirtämään toisen kortin sinuun päin. Siirrä kortti pois tai hyväksy se riippuen siitä, onko tämä katsojan tempun alussa valitsema pelikortti. Pyydä lopuksi katsojaa kertomaan tempun alussa valitsemansa pelikorttinsa. Käännä tämän jälkeen tämä viimeinen kortti ympäri, jolloin huomataan, että se on katsojan valitsema kortti.
Historiaa
Olen keksinyt (löytänyt) yllä olevan idean joskus 2000-luvun alussa, kun tutkin montako Monge-sekoitusta tulee erikokoisille pakoille tehdä, jotta pakka palautuu takaisin lähtöjärjestykseen. Temppu on siis jo yli 20 vuotta vanha. Esitin tätä keikoilla, joissa saattoi pelikorteilla ihmisiä viihdyttää. Temppu on suomen kielellä julkaistu vain kaksi kertaa erittäin harvinaisissa julkaisuissa, joita ei ole käytännössä ollut mahdollisuus ostaa mistään (Makeri, heinäkuu 2020 ja JokeriExtra, heinäkuu 2022) Tämä on siis ensimmäinen kerta, kun ideani julkaistaan suomen kielellä siten, että se on periaatteessa kenen tahansa löydettävissä ja luettavissa.
Monge-sekoituksen on kehittänyt tai paremminkin löytänyt ranskalainen matemaatikko Gaspard Monge (9.5.1746–28.7.1818). Mongella on oma historiansa matematiikan kehittäjänä. Löydät hänestä juttuja matematiikan historiakirjoista, esimerkiksi Tieteiden kuningatar osa II, etenkin kappale Ranskan vallankumouksen matemaatikot (sivut 654–694). Hänen nimeään kantava pelikorttisekoitus on vähemmän tunnettu sivujuoni, jota et matematiikan kirjoista usein löydä. Monge-sekoituksen matematiikkaa pohditaan W. W. Rouse Ballin kirjassa Mathematical Recreations and Esseys (1892). Kirjasta on olemassa Dover-kustantamon edullinen uusintapainos.
Koska korttipakan käyttäytyminen Monge-sekoituksessa muuttuu pakan koon mukaan, vaihtoehtoja erilaisille ilmiöille on paljon. Kun löysin tämän ilmiön yli kaksikymmentä vuotta sitten, olin utelias tietämään, onko kukaan aiemmin käyttänyt Monge-sekoitusta juuri näin, että tehdään sekoitus vain muutamia kertoja ja muistetaan, mihin järjestykseen kortit nyt menevät. Vasta pari vuotta sitten löysin Friedrich Stutzin Taikurin käsikirjasta tempun nimeltään 12 kortin arvaus (sivut 183–184) (** . Siinä käytetään kolmeakymmentäkahta pelikorttia ja muutaman turhan vaiheen jälkeen yhtä Monge-sekoitusta, jonka jälkeen taikuri löytää pöydälle levitetystä pakasta katsojien aiemmin valitsemat pelikortit. Taikurin täytyy muistaa tai tehdä hyvä luntti siitä, mihin järjestykseen 32 korttia menevät yhdellä Monge-sekoituksella. Tempun ohjeet on kirjoitettu tai käännetty suomeksi monimutkaisesti, mutta Monge-sekoituksen pystyy tekstistä tunnistamaan.
Martti Sirén on hämeenlinnalainen taikuri, tietokirjailija, työpajakouluttaja, taikuuden historian penkoja ja tarinoiden kertoja, joskus myös 1700-luvulle ulottuvien ja myös englanninkielisissä lehdissä julkaistujen tarinoiden kertoja. Martti Sirén on kirjoittanut neljä kirjaa matemaattisista taikatempuista ja pitänyt matemaattisten taikatemppujen työpajoja opettajille yli viidentoista vuoden ajan.
(* Lukijalla voi pohtia, tuleeko Monge-sekoituksesta käyttää ollenkaan nimitystä sekoitus, jos korttien järjestys on aina tiedossa. Eikö sekoituksen tulisi olla sellainen, että korttien järjestys ei ole sekoituksen jälkeen tiedossa? Normaalissa tilanteissa, vaikkapa korttipeleissä, korttien järjestys ei ole yleensä tiedossa oikeastaan koskaan. Ja jos emme alun perin tiedä korttien järjestystä, emme sitä taatusti tiedä sekoituksen jälkeenkään, vaikka tietäisimme, miten kortit sekoituksessa siirtyvät.
(** Friedrich Stutz, ZAUBERN vuodelta 1979; Taikurin käsikirja, Karisto. Suomennos Hannu Väisänen. Ensimmäinen painos 1983, toinen painos 1984 ja kolmas 1992. Stutzin kirja oli aikoinaan ehkä paras suomen kielellä ilmestynyt taikurikirja, ja on edelleen yksi parhaimmista.
Osa 1: Pakottavia taulukoita ja paradoksipapereita Dimensio-lehdessä 8.9.2022
Osa 2: Viisi viiriäistä ja kaksi kelmiä Dimensio-lehdessä 20.11.2022
Osa 3: Suklaakarkkeja sammosta Dimensio-lehdessä 29.11.2022
Tilaa Dimension uutiskirje – saat sähköpostiisi aina kuunvaihteessa koosteen tuoreimmista artikkeleista