Ammattimatikka-kyselystä ja ajatuksia matemaattisista valmiuksista
Ammatillinen koulutus on muutosmyllerryksessä monella tapaa. Ammatillisen koulutuksen matemaattisten aineiden opetuksen järjestämisen tapoja ja opiskelijoiden matemaattisia valmiuksia on kartoitettu kyselyllä, joka tehtiin yhdeksi päänavaukseksi ja keskustelun pohjaksi. Aihepiirin käsittelyyn liittyy myös mielipidekysymyksiä ja monitahoisia näkemyksiä.
Artikkeli on julkaistu aikaisemmin Dimensiossa 4/2018.
Toista vuotta sitten polkaisimme Hannele Mannin ynnä muiden kanssa kyselyn matematiikasta ammatillisessa koulutuksessa. Taustalla oli Stadin ammattiopiston useamman toimipaikan matemaattisten opettajien tapaaminen, jossa Hannele keksi idean yhteisestä Facebook-ryhmästä. Miltei samalla virisi myös ajatus opettajille suunnatusta kyselystä, jolla selvitettäisiin tilannetta ammatillisen koulutuksen matematiikan opiskelussa yleisemminkin. Tavoite oli kartoittaa opiskelijoiden valmiuksia opiskeluun, kokemuksia ja käsityksiä integroinnista ammattiaineiden ja matemaattisten aineiden välillä sekä ajatuksia tieto- ja viestintätekniikasta, yhteisopettajuudesta ja oppimateriaaleista. Lähtökohta kartoittamiselle ja kyselylle oli keskustelun avaaminen, ei tieteellisen tutkimuksen tekeminen. Kyselyn linkkiä jaettiin ammatillisessa koulutuksessa toimiville opettajille sekä esimerkiksi Ammatilliset erityisopettajat -sähköpostilistalla (sinne suuntaan vielä kiitos linkin jakamisesta). Vastauksia tuli reilut 50 ammatillisen koulutuksen eri alojen opettajilta, joskaan kaikki eivät vastanneet kaikkiin kysymyksiin. Kyselyn kysymyksiä ei ole suoraan liitetty tähän artikkeliin, mutta ne olisi hyvä lukea pohjustukseksi. Kysymykset ovat nähtävissä osoitteessa: https://tinyurl.com/yabyuhew
Kvantitatiiviset kyselyn lopputulemat ovat melko selviä, tosin liittyy niihinkin tulkinnanvaraisuutta. Kvantitatiivista aineistoa tarjoavaan ”selvään luokitteluun” liittyy määrittelykysymyksiä, kuten mikä on heikon täsmällinen merkitys ja niin edelleen. Lisäksi luokittelu voi liian yleistävää.
Kvalitatiiviset kyselyn lopputulemat ovat tulkinnanvaraisempia. Mikä koetaan tärkeäksi tai tärkeämmäksi? Kommenttien tai asioiden ulos rajaaminen ei ole kovin helppoa.
Olen kuitenkin pyrkinyt tiivistämään tähän lyhyen yhteenvedon kyselyn sadosta sekä käsittelemään sen pääkysymyksiä. Tähän pääkysymysten käsittelyyn liittyy runsain höystein yleistä ja omaa pohdintaa. Artikkelin alkuosa on strukturoidumpi keskittyen kyselyn selvempiin kvantitatiivisiin lopputulemiin, loppuosassa taas käsittelen rönsyävämmin monitahoisia kysymyksiä.
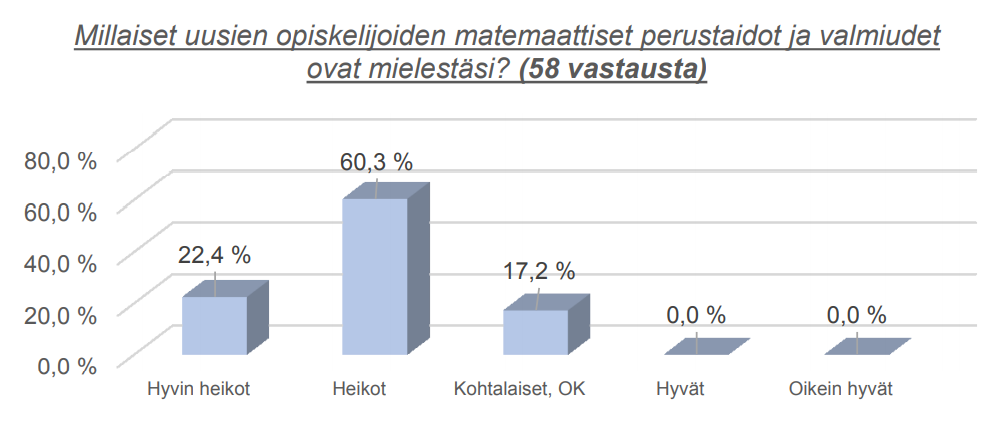
Opiskelijoiden heikot matemaattiset perustaidot ja valmiudet
Huomiota herättävää on yleinen huoli ammatillista koulutusta aloittavien opiskelijoiden matemaattisten perustaitojen ja valmiuksien heikkoudesta. Kuva 1 ja kaavio kertonevat enemmän kuin tuhat sanaa, arvioijina siis ammatillisen koulutuksen eri aloilla työskenteleviä opettajia.
Osaltaan tätä heikkoa lähtötasoa selittänevät kasvaneet sisäänottomäärät, osaltaan yleinen kehityskin. Esimerkiksi Liisa Näverin muutaman vuoden takaisessa väitöskirjassa todettiin, että peruskoulun päättävien matemaattiset taidot ovat heikentyneet sukupolven aikana (Liisa Näveri, 2009, Aritmetiikasta algebraan: Muutoksia osaamisessa peruskoulun päättöluokalla 20 vuoden aikana, Helsingin yliopisto), ja tästä kehityksestä on puhuttu ja uutisoitu viime aikoinakin.
Arviotaan opiskelijoiden perustaidoista ja valmiuksista pystyi tarkentamaan seuraavassa kyselyn kohdassa. Pyrin luokittelemaan näitä jatkovastauksia, joissa korostui kaksi pääteemaa. Toisessa tuotiin esiin heterogeenisuutta opiskelijoiden välillä (31
Yleisarvioinneista voi olla hyötyä, mutta ne yksistään eivät tavoita todellisuuden kirjavuutta ja sävyjen maailmaa. Mainittu heterogeenisuuden esille nouseminen nostaa myös kriittistä sormea kyselyn laadintaa kohtaan: “On vaikeaa arvioida yleisesti, yhtenä ”könttänä” ammatillisen koulutuksen opintoja aloittavien opiskelijoiden matemaattisia perustaitoja ja valmiuksia…” Ehkä tuo kysymys olisi tullut jakaa muutamaksikin täsmennetymmäksi kysymykseksi. Toisaalta taas suurin osa ”jatkovastaajista” korosti heikkoja perustaitoja, ei heterogeenisuutta. Kuitenkin – näin jälkiviisauden jalossa valossa – vinkkaavat nämä puheena olleet jatkovastaukset tai täsmennykset selvästi siihen, että kysymys “Millaiset uusien opiskelijoiden matemaattiset perustaidot ja valmiudet ovat mielestäsi?” on liian yhteen muottiin ahtava. Mukana on myös tietotaidollisesti eteviä opiskelijoita.
Opiskelijoiden itseohjautuvuudesta
Valmiuksien teemaan liittyy myös kyselyn viides kysymys opiskelijoiden itseohjautuvuuden arvioinnista (Kuva 2). Itseohjautuvuutta havainnollistettiin etätehtävien palauttamisella, esimerkiksi keskimmäinen arviointikategoria kuului kokonaisuudessaan: ”Itseohjautuvuus melko ok. Esimerkiksi noin puolet tekee sovitun etätehtävän.”
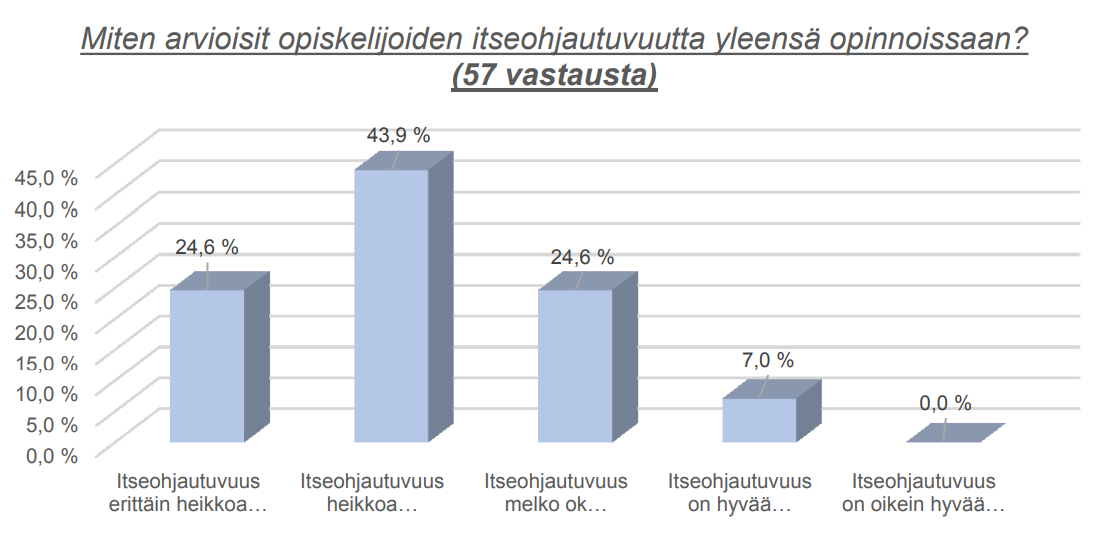
Arvioinneissa on hajontaa selvästi. Suurin osa vastaajista kokee itseohjautuvuuden heikoksi, mutta noin neljännes on arvioinut sen olevan ”melko ok”, ja 7 prosenttia on arvioinut itseohjautuvuuden hyväksi. Tämä viitannee siihen, että eri aloilla suhtaudutaan eri tavoin opintoihin keskimäärin tai lähtökohtaisesti – muuttuneista opiskelijaksi ottamisen kuvioista ja asian moniulotteisuudesta huolimatta. Moniulotteisuudesta, koska toki opiskelu- ja opetuskulttuuri vaikuttavat, mutta niin vaikuttaa myös alalle hakeutunut tai ajautunut opiskelija-aineskin.
Syiksi ja huomioiksi itseohjautuvuuden arvioinnin taustalla (jatkokysymys kyselyssä) nousivat esimerkiksi seuraavat: “Ohjeiden lukutaito. Oppimisen taidot. Osallistaminen suunnitteluun. Opiskelun elämään ja ammattialaan liittäminen. Ryhmäkoot.” Etätehtävät eivät ole toimineet, oli siis yleinen kokemus, ja näin edelleen. Sivuhuomiona kerrottakoon, että eräässä vastauksessa itseohjautuvuuden haasteet nähtiin myös ammattikorkeakoulun opiskelijoiden kohdalla: kirjallisuuteen perehtymisessä, lähteiden käytössä ja asioiden perustelussa.
Mutta mahtui mukaan hyviäkin kokemuksia itseohjautuvuudesta, monisteen tai verkossa olevien videoiden tuella etenemisestä.
Koontia ja kelailua: Itseohjautuvuudesta
Ammatillisen koulutuksen reformin myötä avainasiaksi nousee opiskelijan itseohjautuvuus sekä sen tukeminen. Edellä käsitellyn valossa tähän tarvitaan uusia eväitä. Miten tukea uudella tavalla, miten tehdä selväksi sitä, että toisella asteella oma vapaus sisältää myös vastuuta? Kuinka motivoida todella mahdollisen ”pakkopullan” suorittamiseen?
Ehkä tarvitaan uudenlaista, itseohjautuvuutta paremmin tukevaa materiaalia? Ehkä erityisesti mainituissa videoissa on potentiaalia, erityisesti ytimekkäissä ja mielenkiintoisissa selkovideoissa. Kyselyn vastauksissa toivottiinkin yleisesti verkkomateriaalien sekä yleensä oppimateriaalien ja ammattilähtöisten materiaalien kehittämistä.
Itseohjautuvuus liittyy itsearviointiin. Kun opiskelijoita on pyydetty arvioimaan osaamistaan AHOT-testissä (Aikaisemmin Hankitun Osaamisen Tunnustaminen), ei ole ollut harvinaista, että opiskelija arvioi osaavansa jonkin asian, mutta kun tätä osaamista lyhyesti koetellaan, käy ilmi, ettei hän osaakaan asiaa. Tällaista ilmiötä voinee nousta yleisesti myös, kun opintosuoritus koetaan siksi kuuluisaksi ”pakkopullaksi”.
Itsearviointi kuitenkin liittyy itseohjautuvuuteen ja voi ehkä olla sen avainasiakin.
Esimerkiksi Pekka Peura on ollut paljon esillä mediassa, ja hänellä on varmasti paljon tarjottavaa myös ammatillisen koulutuksen opiskelun itsearviointiin ja -ohjautuvuuteen. Kuitenkin esimerkiksi nuo AHOT-kokemukset ja kokemukset etätehtävistä ynnä muu kestävämpikin kokeilu kiinnittävät huomiota esimerkiksi siihen, ettei lukiossa organisoitu itseohjautuvuuden systeemi välttämättä toimi ammatillisessa koulutuksessa kovinkaan sellaisenaan. Soveltamismahdollisuuksia silti varmasti on ja ehkä muutaman vuoden kuluttua, uuden opetussuunnitelman sisäänajovaiheen jälkeen, toisella asteella aloittavilla opiskelijoilla on paremmat itseohjautuvuus- ja itsearviointitaidot.
Oleellisilta kysymyksiltä ja asioilta tuntuvat seuraavat: “Miten arvioidaan? Mitä arvioidaan?” Näissä voinee yhdistyä esimerkiksi dynaaminen itsearviointi sekä näytön yhteydessä tapahtuva opettajan arviointi tilanteen ja toimivuuden mukaan. Tärkeältä tuntuu myös kysymys siitä, mitä arvioidaan ja testataan. Onko se perusasian ymmärtäminen vai tosiasiassa jokin muu? Tähän palataan vielä lyhyesti artikkelin lopussa.
Koontia ja kelailua: Dialogista, yhteistyön ja resurssien tarpeesta sekä sekavuuden uhasta
Kyselyn muut kysymykset herättivät monenlaisia ajatuksia, mikä johtui osaksi varmasti erilaisista kokemuksista, osaksi ehkä siitä, että käsitteitä ja asioita miellettiin eri tavoin. Kuinka laajasti asiat määritellään?
Tällaisia teemoja tai aiheita olivat jo sivutut integraatio ammattiaineiden ja matemaattisten aineiden välillä, yhteisopettajuus, ammattiosaamisen näytöt ja matemaattisen osaamisen osoittaminen niissä, matemaattisten aineiden suoritukset työssäoppimispaikoilla, tietotekniikan käyttö ja mahdollisuudet ja niin edelleen.
Muutosmyllerryksessä yhteinen kieli luodaan asioista keskustelemalla: Mistä puhutaan, kun puhutaan matematiikan suorituksesta työssäoppimisessa? Mitä tarkoitetaan integraatiolla? Kuinka jyrkästi nämä mielletään?
Kuinka osittain uudetkin ja kehittyvät ilmaisut ja kysymykset ymmärretään ja määritellään?
Erilaisten kokemusten ja käsitysten ”jännitekentästä” nousee esimerkiksi seuraavia kysymyksiä: Tietotekniikka voi olla avuksi sellaisenaan, mutta eikö siihen voi oleellisesti liittyä myös sosiaalista tekemistä, konkreettista mittaamista ja rakentamista? Integraatio ammattiaineen ja matemaattisen aineen välillä ei ole aina toiminut, mutta eikö se voisi toimia toisella kertaa tai toisella tavalla? Miksi matemaattisten perusasioiden oivaltamiseen ei voisi liittyä konkreettinen tekeminen työsalissa tai – kun asia on hyvin järjestetty – työssäoppimispaikalla tai tietotekniikan hyväksikäyttö? Voisiko tällaisesta lähestymistavasta olla hyötyä myös yleisemmin matemaattisessa opiskelussa? Vaikkei päätä kannata hakata seinään, todistaako epäonnistunut kokeilu kokeilemattomuuden puolesta näissä kysymyksissä?
Muutaman sanan erillispohdintana integraatiosta. Itse suhtaudun aineiden väliseen integrointiin positiivisesti, ja mielestäni lähtökohtaisesti kaikki ammatillisen koulutuksen matemaattinen opiskelu voitaisiin liittää ammattiaineeseen. (Tällä en tietenkään tarkoita sitä, etteikö meitä matemaattisten aineiden opettajia tarvittaisi ammatillisessa koulutuksessa!) Kaikki kyselyyn vastanneet ja aiheesta keskustelleet eivät jaa tätä käsitystä. Puolustan kuitenkin tätä omaa suhtautumistani sillä, että yleisesti ammatillisen koulutuksen opiskelijat arvostavat nimenomaan ammattiainetta ja ovat siitä kiinnostuneita. Ammattioppilaitoksessa näin tulee ollakin, että johtotähtenä on se ammattiaine.
Jos esimerkiksi matemaattisia aineita liitetään ammattiaineen suorittamiseen, ja erityisesti sen näyttöihin, tuntuu selvältä, että tällainen integrointi ”skarppaa” suhtautumista myös matemaattisiin aineisiin. Asioiden liittyminen on selvempää ja opiskelija on motivoituneempi.
Pakko ei ole aina paras motivaattori. Oppiaineiden väliseen integrointiin pakottaminen ei välttämättä toimi hyvin.
Jännitekentän potentiaalit tarvitsevat puitteiden luomista: keskustelua, kokemusten vaihtoa ja resursseja näihin. Mahdollisuuksia tähän on reformin myötä ehkä enemmän. Kyselyn vastauksissa todettiin esimerkiksi jäykkien lukujärjestysten haittaavan integrointimahdollisuuksia, ja nythän lukujärjestykset pitkälti poistuvat. Haasteina voi kuitenkin taas toisaalta olla sekavuus sekä esimerkiksi se opiskelijan todellinen itseohjautuvuus, johon taas tietysti systeemin sekavuuskin voi vaikuttaa.
Keskiössä on dialogin tarve ja resurssien tarve. Eri osapuolten välinen dialogi ”jännitekentässä” tuntuu nousevan pääasiaksi eri suunnista. Tarvitaan siis kehittyvää dialogia, mutta se vaatii inhimillisten resurssien lisäksi myös aikaa ja rahaa – vastauksissa noussut teema ja tosielämän tarve.
Näihin kysymyksiin liittyvä dialogin ja yhteisen määrittelyn tarve ulottuu myös laajemmalle, esimerkiksi artikkelin alun kysymykseen heikoista perustaidoista. Näiden heikkojen perustaitojen taustalla voi olla hyvinkin erilaisia peruskoulun päättötodistuksen arviointeja, vieläpä kun valmentavan koulutuksen nopeatahtinen peruskoulun suorittaminen on mukana kasvavalla volyymilla.
Millä dialogilla ja yhteisellä määrittelyllä toiselle asteelle hakevien ja siellä aloittavien opiskelijoiden taustatiedot saataisiin yhdenmukaisemmiksi ja vastaamaan visummin sitä, mitä niiden tulisi vastata? Aiheet ulottuvat laajalle, esimerkiksi myös ammatillisesta koulutuksesta jatko-opintoihin hakemiseen.
Tämä nostaa esille yleisessäkin mediassa olleet kysymykset peruskoulun yhteisestä päättökokeesta tai pääsykokeiden aseman takaisin tulemisesta tai vankistamisesta. Yhteinen kieli ei tarkoita sitä, että asioista oltaisiin aina samaa mieltä, mutta ainakin joissain perusasioissa ja kiinnekohdissa tarvitaan kaiketi selkeää yhdenmukaisuutta.
Koontia ja kelailua: Eriyttämisestä ja omista poluista
Eriyttämiselläkin voi olla erilaisia muotoja. Kysymys siitä, kuinka eriyttää opiskelijoita toimivilla tavoilla, kumpuaa kyselyn vastauksista. Eriyttäminen nousi esille kyselyn vastauksissa eri tavoin: tasoryhmäajatteluna, T1-suoritusten tukemisena (Tyydyttävä 1 eli että tähdätään ”läpipääsyyn”) sekä rauhallisemman oppimisympäristön hakemisena.
Eriyttäminen voidaan tietysti mieltää laajasti, se voi olla enemmän tai vähemmän järeää tai huomattavaa, esimerkiksi tehtäviin tai fyysiseen tilaan perustuvaa. Myös eri opiskeluryhmiin eriyttäminen nousi esiin keinona kyselyn vastauksissa, vaikkei se ole inkluusion mukaista eikä ”muodikasta”. Mutta eikö hyvä kysymys usein ole: mikä toimii?
Toisaalta taas eriyttäminen – jälleen palataan käsitteen määrittelyyn ja ”yhteiseen kieleen” – voi liittyä osaltaan myös yksilöllisiin opintopolkuihin, jotka taas ovat ehdottomasti niin sanotusti päivän sanaa ja kehittyvää toimintakulttuuria.
Kyse on yksilötason järjestelyistä, joihin tarvitaan yksilöä mukaan. Pääkysymyksiä nousee: Kuinka opiskelijassa herätetään sisäinen todellinen motivaatio? Kuinka sitä liekkiä pidetään yllä, kuinka opiskelijaa kannustetaan? Kuinka opiskelija todella osallistetaan opintojensa suunnitteluun?
Ammatillisessa koulutuksessa näihin kysymyksiin pyritään tarjoamaan vastaukseksi HOKSia, joka tarkoittaa henkilökohtaista osaamisen kehittämissuunnitelmaa. HOKS-käytäntöä otetaan paraikaa käyttöön ja kehitetään.
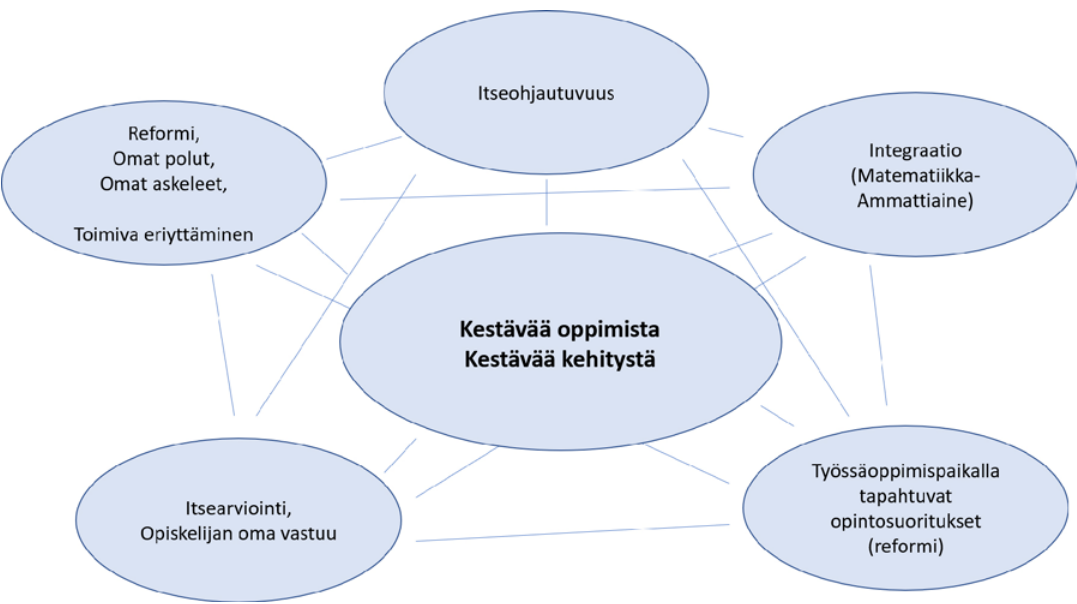
Omien polkujen kulttuuri korostaa keinojen toimivuutta käytännössä, yhdessä ja yksin. Toisaalta tilanne myös suorastaan tuntuu vaativan erilaisten valmiiden polkumallien luomista (esimerkiksi T1-polku tai jatko-opintoihin tähtäävä polku). Tällaisessa maailmassa eriyttäminen tulee ehkä mieltää ja määritellä laajemmin.
Koontia ja kelailua: Yksi yhteenveto
Kaiken kattavaa kaavaa ei ole käytännön tilanteiden kannalta. Kysymysten kenttä on monitahoinen, eikä jokaiseen tilanteeseen ole samaa ratkaisua. Vastauksissa tuotiin esille esimerkiksi sitä, miten työssäoppimispaikat vaihtelevat. Tämä luonnollisesti osaltaan vaikuttaa siihen, miten työssäoppimiseen voi yhdistää esimerkiksi matemaattisia opintosuorituksia.
Työssäoppimispaikkojen vaihtelevuuteen liittyy myös se peruskysymys, miten paljon kullakin työssäoppimispaikalla voidaan ja osataan – tosiasiassa ja todellisten resurssien pohjalta – opiskelijaa tukea ja ohjata. Tämä nostattaa parven eri kysymyksiä, jotka liittyvät tämän artikkelin aiheisiin mutta myös laajemmin yhteiskunnallisiin kysymyksiin.
Keskiössä on oppiminen ja sen myötä kaikki kehitys. Miten varmistetaan oppimisen ja opiskelun laatu sekä estetään tunne siitä, että opintosuorituksia lätkitään miten sattuu? Uusi rahoituksen malli esimerkiksi on aiheuttanut huolta tällaisesta kehityksestä.
Tässä palataan mielestäni myös aiemmin sivuttuun itseohjautuvuuteen: Mikä on tärkein kriteeri matemaattisessa opintosuorituksessa? Onko se tehtävätyyppien toistaminen vai karsitusti pääasian tai pääasioiden ymmärtäminen? Ymmärtäminen taas vaatii itseohjautuvuutta. Ollaan positiivisen kehän äärellä.
Perusasioiden ymmärtäminen on tärkeää myös soveltamisen kannalta, jonka mahdollisuudet kasvavat tietotekniikan kehittyessä: mistä on kyse, mitä mitataan ja lasketaan. Eikö tällöin oleellisempaa ole ymmärtää perusasia, kuten millä tilavuutta mitataan, kuin muistaa hetkellisesti kaava ulkoa?
Nivelvaiheen yhteistyö eri tasojen ja tahojen kesken voisi ehkä tarjota vipuvoimia ja vauhtiaskeleita sille, että saataisiin homma yleensä niin sanotusti lentoon. Ehkä erityisesti perusopetuksen ja ammatillisen koulutuksen kesken?
Hokkuspokkus-helposti ei homma hoidu, mutta yhteistyössä voisi olla monenlaistakin positiivista potentiaalia ja dimensiota, esimerkiksi opiskelijoiden ohjaamisessa ja materiaalien laatimisessa.







