Heinäkuun pulmat 2023: Katkaistun kartion jako
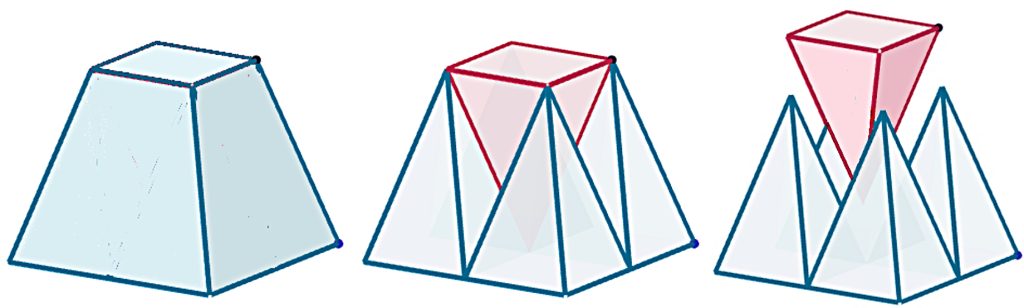
Suoran katkaistun neliöpohjaisen kartion korkeus on h, suuremman pohjan sivu s ja pienemmän pohjan sivu s – 1, missä s = 2, 3, 4, …. Jaetaan kumpikin pohja yksikköneliöiksi ja piirretään kukin yksikköneliö pohjana suora kartio, jonka korkeus on h. Jos käytössäsi on jokin sopiva palikkasarja, niin ryhdy tutustumaan tilanteeseen rakentelemalla muutamia kartioita ennen kuin siirryt tehtäviin.
Tulostettava versio pulmista (pdf)
Tehtäviä:
1. Kuvassa katkaistun kartion suuremman pohjan sivu on kaksi. Silloin pieniä kartioita on yhteensä viisi.
Kuinka monta pientä kartiota on, kun katkaistun kartion suuremman pohjan sivu on 3 tai 4?
Käytä rakennuspalikoita tai keksi jokin muu malli kartioiden lukumäärän selvittämiseksi.
2. Keksi sääntö pikkukartioiden määrän laskemiseksi. Ilmoita sääntösi lausekkeena s:n avulla.
3. Mikä on pienen kartion tilavuus, kun h = 2? Entä katkaistun kartion tilavuus, kun s = h = 2?
4. Kuinka suuri on kuvan mukaisen viiden pienen kartion yhteenlasketun tilavuuden suhde katkaistun kartion tilavuuteen?
5. Miten suhdeluku riippuu katkaistun kartion korkeudesta?
6. Kirjoita lauseke pienen kartion tilavuudelle h:n lausekkeena.
7. Kirjoita lauseke katkaistun kartion tilavuudelle s:n ja h:n funktiona.
8. Mitä lukua pikkukartioiden tilavuuksien summan ja katkaistun kartion tilavuuden suhde lähestyy, kun s kasvaa rajatta?
Dimension pulmatehtävien ratkaisut MAOL ry:n sivuilla (vain jäsenille).







