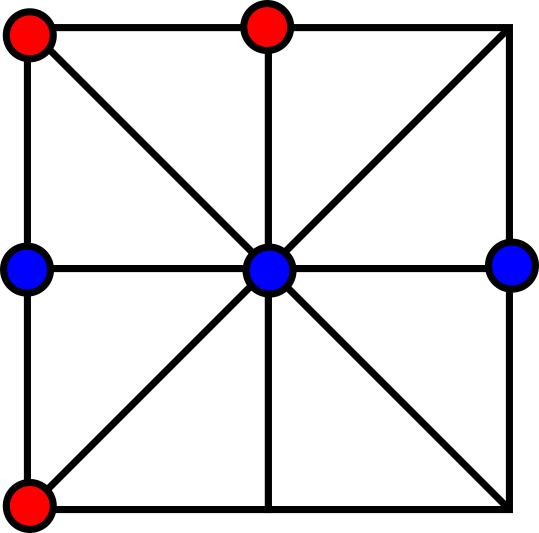
Japanilainen tikkukertolasku
Erilaisia kertolaskualgoritmeja tunnetaan paljon. Japanilainen tikkukertolasku perustuu toimintavälineisiin tai piirrokseen. Idean löysin pedanetistä [1].
Menetelmä perustuu tikkujen asettelemiseen tai viivaryhmien piirtämiseen (kuva) ja leikkauspisteiden laskemiseen [2]. Sekä kertoja että kerrottava esitetään kaksinumeroisten lukujen tapauksessa kaksiosaisella ryhmällä, jonka ensimmäisessä osassa on kymmennumeroa ja toisessa ykkösnumeroa vastaava määrä viivoja. Tulon numerot saadaan laskemalla leikkauspisteiden määriä. Jos tekijöiden kymmen- ja ykkösnumerot ovat pieniä, niin tulo voidaan lukea suoraan leikkauspisteiden määristä: sadat, kymmenet ja ykköset (vasen kuvio). Jos määrä on kymmenen tai suurempi, kymmenluku on lisättävä seuraavaksi suuremman lukuyksikön ilmoittavaan lukuun.
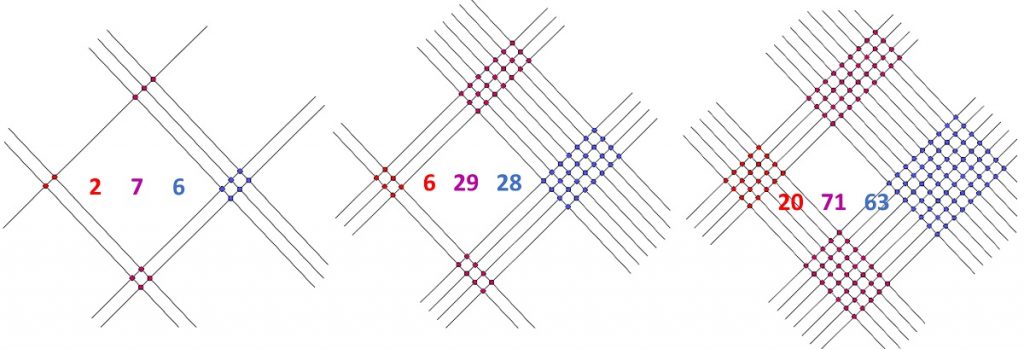
Menettelyä voitaisiin jatkaa kolminumeroisiin lukuihin ja pitemmällekin, mutta leikkauspisteiden laskeminen kävisi vähitellen kovin työlääksi. Kaksinumeroisten lukujen kertolaskua esittävä malli sopisi myös binomien kertolaskun laskemiseen. Kuva 1 voisi siten esittää tuloja (x + 2)(2x + 3) = 2x2 + 7x + 6, (3x + 4)(2x + 7) = 6x2 + 29x +28 ja (4x + 7)(5x + 9) = 20x2 + 71x + 63 tai (x4 + 2x)(2x3 + 3x) = 2x7 + 3x5 + 4x4 + 6x2 jne. Tällöin pitää vain erikseen selvittää, mitä muuttujan potenssia kukin leikkauspisteryhmä esittää.
Verkossa on useita tikkukertolaskua selostavia videoita. Niitä löydät esimerkiksi haulla ”Japanese stick multiplication”. Tikkumenetelmä ei liene vanha, sillä siitä on mainintoja vain ihan viimeisten vuosikymmenien ajalta [4]. Sitä nimitetään myös kiinalaiseksi tikkukertolaskuksi [5]. Ehkä sen vuoksi, että kiinalaiset ovat käyttäneet tikkuja laskulaudalla jo toista tuhatta vuotta sitten.
Lähteitä:
[1] Voutilainen, Hanna: Metka japanilainen tapa laskea kertolaskuja osoitteessa
https://peda.net/p/hanna.voutilainen/mljv/envm/jtlk, viitattu 27.7.2021.
[2] Paulaharju, Tatu: Ällistyttävä tapa laskea – näin Japanissa kerrotaan osoitteessa
https://www.is.fi/tiede/art-2000000561265.html, viitattu 29.7.20121
[3] Katso Geogebra-materiaalia Japanilainen tikkukertolasku osoitteessa https://www.geogebra.org/m/egjqz9za
[4] Delbert, Caroline (2020): The Japanese Way to Multiply Is So Much Cooler Than Ours osoitteessa
https://www.popularmechanics.com/science/a32131826/ancient-multiplication-method/, viitattu 30.7.2021.
[5] Pearce, Kyle (2017): Why Japanese multiplication works osoitteessa
https://tapintoteenminds.com/japanese-multiplication/, viitattu 30.7.2021