Matemaattisia taikoja ja variaatioita muistilehtiöstäni, klassiset matemaattiset taikatemput, osa 10: Kruskalin periaatetta kahdella tempulla
Legohahmot läjään
Tempun kuvaus lyhyesti
Lähes täysin vapaiden valintojen jälkeenkin katsojien LEGO-hahmot päätyvät saman pelikortin päälle.
Valmistelut
Tarvitset mieluimmin A5-kokoisen korttipakan. Tämän jutun lopussa kerron, mistä niitä saa. Lisäksi tarvitset LEGO-hahmoja tai pelinappuloita. Niitä löytänet ohjeitta.
Jos sinulla on uusi korttipakka, sekoita se oikein hyvin. Jaa pakka pöydälle pitkäksi mutkittelevaksi radaksi kuvapuoli ylöspäin. Yhdistä pöytiä, pulpetteja, tai mitä vain tasoja, jotta saat kaikki kortit yhdeksi mutkittelevaksi riviksi ikään kuin sinulla olisi valtaisa pelilauta. Jos tila on loppua kesken, ota pakasta pois kuvakortteja.
Laita korttirivin päähän purkillinen LEGO-hahmoja. Mikäli et saa lainatuksi riittävästi hahmoja, voit käyttää pelinappuloita tai vaikkapa Fazerin sekalaiset -karkkeja. Kaiken tuon teet ennen kuin esitys/luento/oppitunti alkaa.
Tempun kulku
Jokainen oppilas tai katsoja ottaa LEGO-hahmon ja asettaa sen mihin tahansa ensimmäisen kymmenen pelikortin päälle. Katsoja lähtee kuljettamaan LEGO-hahmoaan kuin pelilaudassa eteenpäin.
Ensimmäisen siirron pituus määräytyy sen pelikortin arvon mukaan, johon hän hahmonsa laittoi. Jos LEGO-hahmo asetettiin ruutukuutosen päälle, katsoja laskee kuusi korttia eteenpäin. Lautapelien tapaan laskeminen aloitetaan seuraavasta kortista. Katsoja päätyy uuden kortin päälle. Kortin arvo kertoo, kuinka pitkän matkan LEGO-hahmoa viedään.
Näin jatketaan, kunnes katsoja on edennyt viimeisten korttien luokse. Aivan lopussa katsoja huomaa olevansa kortin päällä, jonka arvoa ei ole mahdollista enää laskea loppukorteilla. Laskeminen jäisi kesken. Niinpä katsoja jättää LEGO-hahmonsa kortin päälle, jonne edellinen laskeminen hänet johdatti.
Otetaan esimerkki. Kortit on jaettu alla olevan kuvan mukaisesti. Matka alkaa kuvassa yläriviltä ja aluksi vasemmalta oikealle. Ensimmäisen rivin jälkeen laskeudutaan toiselle riville, jota edetään oikealta vasemmalta oikealle. Kuvan vihreät nuolet opastavat suunnat ja käännökset.

Seuraavassa kuvassa LEGO-hahmoja on jo aseteltu ylimmän rivin pelikorttien päälle.
Siniharmaa Batman-hahmo on ristiseiskan päällä. Batman-hahmon laittaja laskee seitsemän korttia eteenpäin (ruutukuusi, pataneljä, herttakuusi, ruutuässä, herttaviisi, ruutukahdeksan ja pata sotilas) ja päätyy toiselle riville patasotilaan päälle.
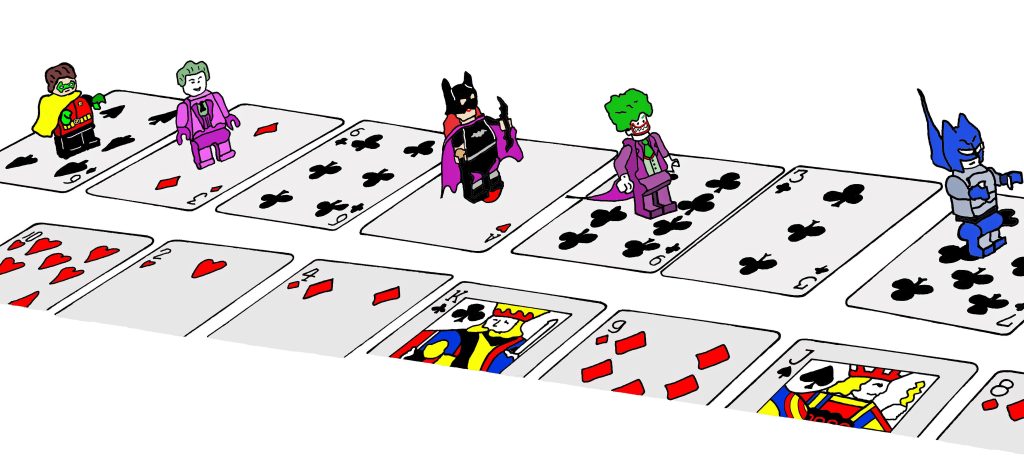
Koska sotilaan arvo on yksitoista, Batmanin matka jatkuu yksitoista korttia eteenpäin. Päädymme ristikymppiin. Kymmenen korttia eteenpäin ja olemme herttarouvan päällä. Tästä kaksitoista korttia eteenpäin, olemme ristirouvan päällä ja aivan lähellä viimeisen rivin loppua, joten matkaa ei voi enää jatkaa.
Entäpä sitten?
Taikuus, tai ainakin suuri hämmästys tulee siitä, että kun kaikki LEGO-hahmot ovat tehneet retkensä, lähes kaikkien matka on tuonut heidät alarivin ristirouvan päälle! Ylärivillä on kolme korttia, joilla pääsee alariville muualle kuin ristirouvan päälle. Yllä oleva esimerkki on todellinen sekoitettu pakka. Kun sekoitat oman pakkasi, saat omat reitit, mutta nekin päättyvät, joko kaikki tai suurin osa, yhteen korttiin.

Lisää tarkkuutta
Jos haluat, että ylärivin lähtöpaikasta riippumatta kaikki päätyvät saman kortin päälle, poista pakasta kaikki kuvakortit tai siirrä ne pakan loppupuolelle. Jos haluat, että korteista rakennettu ketju on pitkä, voit ottaa kahden korttipakan numerokortit (ässästä kymppiin) käyttöön. Arvoltaan pienet kortit tai suurempi määrä kortteja lisää kaikkien reittien yhdistymistodennäköisyyttä.
Tiedän mihin päädyit
Seuraava on yhtä paljon temppu tai haaste kuin peli. Idea muistuttaa edellistä temppua. Nyt kaikki tapahtuu nopeammin, korttipakan jakamisen aikana. Väärinlaskemisen määrä kasvaa, mutta silti suurin osa katsojista päätyy samaan korttiin.
Tempun kulku
Pöydälle jaetaan pelikortteja yhteen pinoon, kuvapuoli ylöspäin. Katsoja valitsee kymmenen ensimmäisen kortin jakamisen aikana yhden korteista omaksi kortikseen. Jos valittu kortti on hertta viisi, hän laskee mielessään seuraavat viisi korttia. Jos viides kortti on kolmonen, laskee katsoja mielessään kolme jaettavaa korttia eteenpäin. Katsojat tekevät laskunsa siten, etteivät paljasta laskemisiaan. Tällä tavalla edetään kaikki kortit lävitse, kunnes pakan loppupäässä katsojat huomaavat, etteivät he pysty laskemaan seuraavaa lukua kokonaan: edellinen laskenta päättyi vaikkapa ristijätkään (11), eikä pakassa enää ole yhtätoista korttia. Asian hahmottamista helpottaa, jos taikuri jakaa viimeiset noin kymmenen korttia riviin pöydälle.

Miten se tehdään?
Temppu voidaan ja se kannattaakin tehdä sekoitetulla pakalla ja A5-kokoisilla korteilla. Korttien jakaja, taikuri, valitsee itselleen oman kortin, minkä vain, josta eteenpäin hän laskee mielessään ylläkuvatulla tavalla kortteja, samalla kun jakaa kortteja pöydälle. Kun katsojat keskittyvät laskemaan omaa reittiään, kukaan ei huomaa, että taikuri laskee myös. Niinpä katsojilla ei tempun lopussa ole mitään käsitystä siitä, miten taikuri tietää, mihin katsojien laskenta päättyi.
Koko temppu voidaan tehdä niin, että yksi katsojista sekoittaa pakan ja jakaa kortit pöydälle. Tällöin taikuri vain seuraa vierestä ja keskittyy omaan laskemiseensa. Tämä lisää tempun mystisyyttä: taikuri ei edes koskenut pakkaan, mutta hän silti tiesi, mihin suurin osa katsojista laskuillaan päätyi.
On erittäin suuri todennäköisyys sille, että jakajan ja katsojien laskemat tiet kohtaavat. Kun kaksi tai useampi laskureitti on yhdistynyt, ne jatkavat loppuun saakka samaan viimeiseen korttiin. Jos sekoitat pakan itse, voit lisätä todennäköisyyttä päätyä samaan korttiin siirtämällä kuvakortit pakan loppupäähän. Tämän voi tehdä samalla kun muutoinkin sekoittaa pakkaa.
Tempputekniikkaa
Jotta temppu onnistuisi, tulee kortteja jakaa pöydälle rauhallisesti. Katsojien tulee tietää, mitä hän on tekemässä. Jotta temppua olisi helpompi seurata, se kannattaisi tehdä isoilla pelikorteilla. Jutun kuvituskuvassa tuolla ylempänä taikuri käyttääkin A5-kokoa olevia kortteja.
Laskemista kannattaa harjoitella pienellä jakokierroksella ennen kuin lähdetään jakamaan koko pakkaa. Jakamista voi pöydän ääressä seurata ja samalla laskea jopa toistakymmentä henkilöä.
Kruskalin laskenta
Yllä olevien kahden tempun todennäköisyyksiin perustuvan ilmiön on löytänyt ilmeisesti ensimmäisenä venäläisamerikkalainen matemaatikko Eugene Borisovich Dynkin 50-luvulla (Евгений Борисович Дынкин; 11.07.1924–14.11.2014). Amerikkalainen fyysikko ja matemaatikko Martin David Kruskal (28.9.1925-26.12.2006) löysi samaisen ilmiön 1970-luvun alussa ja esitteli sen korttitemppuna Martin Gardnerille. Gardner julkaisi tempun Karl Fulvesin The Pallbearers Review -taikurilehden kesäkuun numerossa vuonna 1975 (sivut 967 ja 970) nimellä The Kruskal Principle. Gardner totea, että todennäköisyys sille, että sekoitetulla korttipakalla kaksi laskentaketjua yhdistyvät, on 5/6, eli 83 prosenttia. Fulvesin hyvin pienilevikkinen lehti oli ensimmäinen julkaisu, jossa Kruskalin löytö on julkaistu. Laajempaa huomiota ilmiö sai, kun Martin Gardner julkaisi samaisen tempun selityksineen Scientific American -lehden Mathematical Games -palstallaan helmikuussa 1978 ja uudestaan kirjassaan From Penrose Tiles to Trapdoor Ciphers vuonna 1988 (W. H. Freeman Co., New York). The Pallbearers Review -lehdet on julkaistu kolmena kirjana vuonna 1993 (L&L Publishing), laajemmalla levikillä kuin alkuperäisillä lehdillä aikoinaan oli.

Englantilainen matemaatikko John Pollard on löytänyt muista tietämättä saman menetelmän ja käytti sitä kryptografiassa. Kruskalin laskennalla on siis sovelluksia aina koodinmurtamisesta taikatemppuihin.
Idea käyttää pelinappuloita ja jakaa kortit riviin pöydälle löytyy ainakin Ehrhard Behrendsin kirjasta The Math Behind the Magic (AMS, 2019, sivu 183) nimellä We are All Friends: The Kruskal Magic Trick.
Mistä on kysymys?
Miten Kruskalin laskenta toimii edellä mainituissa tempuissa? Jokaisessa laskuhypyssä kortista seuraavaan korttiin katsojalla on mahdollisuus osua korttiisi, joten näin tulee vääjäämättä tapahtumaan, jos pelikortteja ja hyppyjä kortista toiseen on riittävästi. Kun reitit ovat osuneet yhteen, ne pysyvät yhdessä loppuun saakka. Sekoitetulla korttipakalla todennäköisyys on noin 80 prosenttia. Aiemmin kerroin, että todennäköisyyttä saa parannettua jo sillä, että kuvakortit siirretään pakan loppupuolelle. Gardner ehdotti, että kuvakorttien arvoksi lasketaan aina kymmenen. Fulves ehdotti kuvakoreille arvoksi viisi, mikä lisännee tempun onnistumisen todennäkysyyttä. Matemaattisesti ratkaisu on hyvä, mutta muutoin en pidä kuvakorttien arvon muuttamista hyvänä ideana. Parempi tapa on poistaa kuvakortit pakasta kokonaan ja laittaa tilalle kaksitoista pienehköä numerokorttia toisessa pakasta, mikäli haluat, että korttipakassa olisi 52 korttia.
Pelikorteista
A5-kokoisia tai suurempia pelikortteja löydät, kun googletat Jumbo pelikortit. Ennen kuin tilaat, katso korttien todellinen koko: myynnissä on tavallisen kokoisia korttipakkoja, joissa kortin maa ja arvo on merkitty tavanomaista suuremmalla fontilla, ja näistäkin käytetään nimitystä Jumbo-kortit. Flying Tiger -myymälöissä on myynnissä edullisia A5-kokoisia korttipakkoja, myös postimyyntinä, mikäli kauppaa ei omassa kaupungissa ole: https://flyingtiger.com/fi-fi/products/playing-cards-3035617
Perinteisen Aprilli-kaupan raunioista nousi ylös Ilon Tähden /Aprilli Lahti osoitteessa Karjalankatu 2, 15140 Lahti (puh 040 6462364). Kauppa aloitti nettimyynnin helmikuun alussa. Tätä kirjoittaessa nettimyymälän valikko on pienehkö, eikä A5-kokoisia pelikortteja siellä ole, mutta heiltä kannattaa kysyä tuotteita, joita netissä ei vielä näy. https://ilontahden.fi/
Martti Sirén on hämeenlinnalainen taikuri, matemaagikko, tietokirjailija, kouluttaja, eteenkin matemaattisten taikatempputyöpajojen kouluttaja, taikuuden historian penkoja, kuvittaja ja tarinoiden kertoja, joskus myös todennäköisyyksiin ja pelikortteihin kietoutuneiden tarinoiden kertoja.
Edellinen taikuriartikkeli: Matemaattisia taikoja ja variaatioita muistilehtiöstäni, osa 8: Möbiuksen rengas







