Kolme oppilastapausta

Tässä artikkelissa kerron kolmesta oppilaasta, jotka kävivät luonani yksityisopetuksessa: ykkösluokkalainen tyttö, kolmasluokkalainen poika ja abiturientti-tyttö. Näistä oppilaista ja monista muista kerron kirjassani Matematiikan osaaminen vahvaksi – Iloa opettamiseen ja oppimiseen. Kirjaan kehittelin myös useita pelejä, jotka vahvistavat lukukäsitettä, yhteen- ja vähennyslaskutaitoa sekä kymmenjärjestelmän ymmärtämistä.

Ykkösluokkalainen

Yksityisopetukseeni tuli tyttö ensimmäisen luokan huhtikuussa. Kun kysyin häneltä, kuinka monta sormea hänellä on toisessa kädessä, hän kosketti sormia yksitellen: ”yksi, kaksi, kolme, neljä… viisi!” Kun näytin neljää helmeä, hän teki samoin: hän kosketti jokaista helmeä erikseen ja totesi ”neljä”.

Huolestuin ja mietin, miten tämä on mahdollista: nämä taidot pitäisi olla hallussa viimeistään ensimmäisen luokan alussa. Näytin hänelle muutamia yhteen- ja vähennyslaskuja lukualueelta 0–10 ja hän laski hitaasti kaikki laskut sormilla. Lukujen 2–10 hajotelmat olivat täysin hukassa. Oppikirjassa oli meneillään jo kymmenalituksia ja kymmenylityksiä sekä laskuja lukualueelta 20–100. Tyttö totesi, että matikka on vaikeaa. Mietin, miten tällaisilla taidoilla varustettu oppilas voi pärjätä toisella luokalla? Mitä voin tehdä hänen auttamisekseen? Sovittiin, että tyttö tulee luokseni tunnin ajan viikossa. Kun vanhemmat tulivat hakemaan, kerroimme, mitä tehtiin ja annoin välineitä lainaksi kotiin.

Koska keväällä oli niin vähän aikaa, johdonmukaista matikkaterapiaa en voinut aloittaa hänen kanssaan. Halusin saada hänelle onnistumisen kokemuksia, joten ryhdyimme pelaamaan tytölle kehittämääni Kumpi saa ekana 10? -peliä. Meillä kummallakin oli kasa kahdenvärisiä linkkikuutioita, yksi pistenoppa ja tyhjä kymmenen munan kenno. Noppaa heitettiin vuorotellen. Heittäjä sai laittaa kennoonsa yhdenvärisiä kuutioita, jotka vastasivat nopan silmälukua. Seuraavalla kerralla laitettiin toisen värisiä kuutioita. Koko ajan tyttö kertoi, kuinka monta kuutiota oli yhteensä kennossa ja kuinka monta puuttui täydestä kympin kennosta. Voittaja oli se, jonka kenno täyttyi ensin. Tekemisen selostaminen ääneen ei ollut tytölle helppoa, mutta vähitellen sekin alkoi sujua. Pelaamisesta tyttö innostui niin, että meinasi tuolilta tipahtaa!

Lukujen 2–10 hajotelmia ja pieniä yhteen- ja vähennyslaskuja tyttö harjoitteli mielellään tekeillä olevilla matematiikan miniLUKO-tehtävillä, kun hänen ei tarvinnut kirjoittaa laskuja paperille. Kotiin annoin lainaan munakenno-pelin ja miniLUKO-tehtäviä ja -pelialustan sekä ohjeita tekeillä olevasta kirjastani lukujen 0–10 opetuksesta. Toivoin, että kotona pelattaisiin ja keskusteltaisiin lukumääristä.

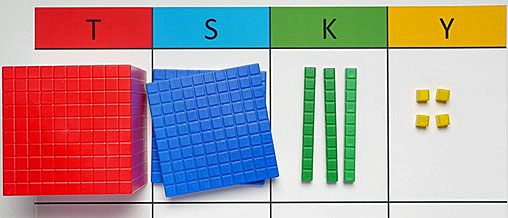
Seuraavaksi pelattiin Kumpi saa ekana 20? -peliä, jossa toimittiin muuten kuin edellä, mutta nyt oli kummallakin täytettävänä kaksi munakennoa. Lisäksi kummallakin oli yksi pistenoppa, viivain ja sinitarraa (katso kuvaa). Pelaaja, joka ensimmäisenä sai molemmat kennonsa täyteen, oli voittaja.
Peliä pelattiin myös taaksepäin niin, että täysistä kennoista otettiin pois arpanopan pisteiden lukumäärän mukaisesti kuutioita. Pelin nimeksi annettiin Kuka saa ekana kennot tyhjäksi?

Lukumäärät 10–20 olivat vielä vaikeita tälle oppilaalle. Eteneminen arpanopan silmälukujen verran eteenpäin ja taaksepäin sujui hitaasti ja oli jopa hauskaa, kun hän vihdoin oppi näkemään suoraan arpanopan pisteiden lukumäärän. Sovittiinkin, että kesäksi annan kotiin muutamia uusiakin peliohjeita sekä ohjeita tekeillä olevasta kirjastani lukujen 0–20 opetuksesta. Syksyllä jatkettaisiin uusin voimin.

Välineet avasivat matematiikan keskeiset käsitteet Pyrylle

Kolmasluokkalaisen Pyryn äiti otti minuun yhteyttä syyslukukauden lopussa. Äiti kertoi, että Pyry oli huomannut olevansa matematiikassa ainakin vähän hidas ja epävarma suhteessa joihinkin kavereihinsa. Pyry oli päätynyt siihen, että hän on huono ja tyhmä matikassa. Tätä käsitystä on ehkä hieman tukenut myös ajoittain tunneilla käytettävät nopeus- ja muut kilpailut, kuten kertolaskujen ”pudotuskokeet”.

Äiti oli huolissaan tilanteesta, sillä matematiikka ja siihen liittyvät ongelmat uhkasivat ajoittain koko koulutyön mielekkyyttä. Äiti pyysi apua, jotta matematiikka asettuisi oikealle paikalleen muiden kouluaineiden joukkoon. Sovimme, että Pyry tulee kerran viikossa opetukseeni.

Ensimmäisellä kerralla tavatessamme, pyysin Pyryä kirjoittamaan isolle paperille sekä helppoja että vaikeita laskuja. Kun haastattelin häntä lisää, kävi ilmi, ettei hän osannut 1. eikä 2. luokan tärkeimpiä käsitteitä, puhumattakaan 3. luokan sisältöjä. Istutin Pyryn rimoista tehdyn kuutiometrin sisään ja ryhdyimme pohtimaan, mitä matikkaa siitä voisi saada. Pyry huomasi, että hän on korkeampi kuin kuutio, joten siitä saatiin alku eri kohteiden mittaamiselle mittanauhalla. Silloin myös huomasin, mitkä luvut olivat Pyrylle vaikeita lukea ja kirjoittaa.

Välineistä intoa ja apua

Keskityimme aluksi alkuopetuksen tärkeimpiin sisältöihin ja Pyry huomasi, että näiden sisältöjen hallinta auttoi häntä myös 3. luokan asioissa. Pojan itsetunto kasvoi ja hymy oli herkässä. Välineiden käytöstä Pyry kiinnostui, kun huomasi, että ne auttavat ymmärtämään sekä lukuja että laskuja.

Annoin vanhemmille vinkkejä AbacoMath-ohjelmasta ja muutamista peleistä. Pyysin vanhempia hankkimaan tärkeitä välineitä, joiden avulla he voivat auttaa Pyryä läksyjen teossa nyt 3. luokalla ja myöhemminkin. Suosittelemani välineet olivat Ten Base -peli, pieni opetuskello, Multilink-kuutiot, värisauvat, uraviivain 0–100, loogiset palat, murtokakut, kymmenjärjestelmävälineet ja desimaaliosat. Opetin myös Pyryn vanhemmille niiden käyttöä. (Kun myöhemmin tapasin Pyryn äidin, hän kertoi, että nämä välineet ja pelit ovat hyvässä tallessa, ne odottavat Pyryn lapsia.)

Pyry kävi opetuksessani noin kerran viikossa sekä 3. luokalla että 4. luokalla. Keskeiset käsitteet selkisivät eikä kotiläksyjen kanssa ollut ongelmia. Tavoite oli saavutettu!

Yläkoulusta lukioon

Tapasin Pyryn perheineen seuraavan kerran sen kesän alussa, jolloin hän lopetti peruskoulun. ”Sain koko yläasteen ajan kiitettäviä matikasta ja syksyllä menen lukioon lukemaan pitkää matikkaa!” Sovimme, että voimme tarvittaessa tavata syksyllä, ja niin teimmekin.
Lukiossa matikan opetus ei sujunut niin hyvin, kuin Pyry oli olettanut. Ongelmana oli myös, ettei matematiikan kokeita palautettu niin, että tehtävien oikeita ratkaisuja olisi annettu oppilaille. Opetin Pyryä muutaman tunnin ajan ja myöhemmin toinen yksityisopettaja tuki Pyryä myös muutaman tunnin verran.
Ylioppilaskirjoituksissa Pyry sai pitkästä matematiikasta magnan. Pyry pääsi heti opiskelemaan kauppatieteitä ja matikka on sujunut yliopistossa hyvin. Hänen mielestään se on ollut lähinnä vanhan kertausta ja muutenkin helpompi ymmärtää, koska se liitetään hyvin käytännön asioihin. Se tuntuu siksi olennaiselta eikä turhalta kaavojen pänttäykseltä.

Matikkaa inhoava Pulmu kiinnostui ja innostui matikasta

Abiturientti Pulmu tuli luokseni paria kuukautta ennen matikan ylioppilaskirjoituksia ja totesi:
”Mä inhoon matikkaa, enkä osaa mitään.” Kysyin vielä tarkemmin, mitä hän ei osaa ja hän jatkoi:
”Joskus siellä ylhäällä on 2 ja joskus 3, enkä tiedä miksi. Mun kaverilla on kämppä, joka on 11 neliöö,
enkä tiedä kuinka suuri se on!”
Tämän jälkeen haettiin autotallista metrin pituisia rimoja, joiden avulla rakennettiin kuutio. Pulmu istui kuution sisällä ja hän ryhtyi kymmenjärjestelmävälineiden avulla pohtimaan kuution kokoa. Kun hänelle selvisi, että kuutio on kuutiometrin kokoinen ja pohja neliömetrin, niin tuli toteamus: ”Ei oo muuten kaverilla iso kämppä!”

Ne ylhäällä olevat kakkoset ja kolmoset tulivat tutuiksi: pinta-ala on kaksiulotteista ja tilavuus kolmiulotteista. Yhdessä avasimme kaikkein olennaisimpia matematiikan käsitteitä konkreettisesti. Kävimme lävitse kymmenjärjestelmän desimaalilukujen osalta. Tarinoiden kautta hahmotimme sanallisia tehtäviä. Muita tärkeitä asioita olivat mittayksiköt ja murtoluvut. Alakoulun matematiikkaa!
Onnistumisen kokemukset kohottivat Pulmun itsetuntoa ja hänen käsityksensä itsestä matematiikan oppijana muuttui. Hän sai intoa tehdä ylioppilaskirjoituksiin valmentavia matematiikan kertaustehtäviä. Ylioppilaskirjoituksissa Pulmu sai lyhyestä matematiikasta cum lauden.

Ylioppilaskirjoitusten jälkeen

Pyysin Pulmua kirjoittamaan oman matikan tarinansa. Tässä otteita hänen kertomuksestaan.

”Itse oon kyllä enemmän kuin tyytyväinen tuloksiin ja siihen että miten mun asenne matikkaa kohtaan on muuttunu. Musta on nykyään enemmänkin kiva ratkasta pulmia ja kattoa mitä osaan, kun että pelkäisin koko ainetta. Itse kirjotuksissa tuli ihan sellanen ´´flow´´ tila, että välillä ihan unohdin missä oon kun olin niin inoissani laskemassa:) ja kokeen jälkeen sanoinkin äitille, että ihan kun oisin ollu jossain leffassa… niin mukavasti se kuus tuntia siellä meni 😀
Matikka on ollu mulle aina tuhottomanvaikeaa pakkopullaa ja oon aina ajatellu ettei mulla vaan ole matikkapäätä ja ns. luovuttanu koko matikan suhteen. Nyt vihdoinkin olen tajunnut etten vaan alunalkaenkaan ole päässyt ihan jyvälle matikassa. Nyt kun olin sulla opetuksessa tajusin että matikassa voi olla näin:

• Opettaja voi herättää kiinnostuksen oppimaan niin, että oppimisesta tulee mielekkäämpää yhdessä tekemistä, ja ongelman ratkaisua.
• Myös asioiden havainnollistaminen auttoi suuresti, koska aikaisemmin matikka on ollut mulle vaan sellaista hauki on kala toistamista sääntöjen puolesta, jotka helposti unohtuu, koska asiaa ei ilmeisesti koskaan ymmärretä (syy-seuraus suhteita).
• Oli myös ihanaa huomata, kuinka ei ollut tyhmiä virheitä, jos en vaikka tiennyt jotain (esim. monta nollaa miljoonassa) koska aina luokassa on tullut sellainen, etten edes viitsi kysyä kun se jo varmaan pitäsi tietää…. opettajat harvoin luokassa kerkee ns. asettumaan oppilaan tasolla ja näyttää ehkä myös oman virheellisyytensä mikä voisi mahdollistaa sellaisen ´´hei ratkaistaampa yhdessä hengen´´.
• Oli ihanaa, kun ei oikeesti tarvinnut esittää osaavansa jotain mitä ei osaa eli sai olla niin tyhmä kun halusi ja siitä sitten lähdettiin yhdessä oppimaan.
• Jos olisin ala-asteella jo saanut peruspohjan matikkaan ja sellaisen oppimisen ilon ois sitä ollu helpompi jatkaa sitten ylä-asteella ja lukiossa. Mutta mulla oli kyllä jo ne ala-asteen jutut ihan hakusessa ja sen takia matikan pohjaa, minkä päälle rakentaa ei oikeastaan ollut. Myös se fiilis matikasta oli aina huono, kun en koskaan osannut mitään… ja kyllähän se latistaa oppimisen iloa,
  jos ei tule onnistumisia.
  Kiitos paljon vielä sinulle, kun sait mun kiinnostuksen ja itseluottamuksen heräämään matikan suhteen.”

Lukion jälkeen

Pulmu toimi lukion jälkeen pari vuotta kouluavustajana luokassa, jossa opiskeltiin matematiikkaa Varga-Neményi-menetelmällä. Hyvien kokemusten siivittämänä Pulmu totesi haluavansa opiskella luokanopettajaksi. Hän pääsikin opiskelemaan luokanopettajaksi, ja oli tyytyväinen valintaansa. Muutaman opettajavuoden jälkeen hän aikoo opiskella erityisopettajaksi.

Kirjallisuutta & lähteet

Hannele Ikäheimo: Matematiikan osaaminen vahvaksi. Iloa opettamiseen ja oppimiseen. ELLI 2021
Hannele Ikäheimo: Materiaalikirja. Matematiikan osaaminen vahvaksi. ELLI 2021
Hannele Ikäheimo & Pieta Voipio: Matematiikan laskustrategioita 0–100. Yhteen- ja vähennyslaskuja lukualueilla 0-10, 0-20 ja 0-100. MiniLUKO-tehtäväkirja. ELLI 2021

Hannele Ikäheimo esittelee Matematiikan osaaminen vahvaksi -kirjaansa kahdella videolla:
https://ellinkauppa.fi/tuote/matematiikan-osaaminen-vahvaksi-videoesittely/