Monikulmioita GeoGebralla

Olin viime syksynä unelmatilanteessa, sillä sain tehdä diplomityöhöni juuri itseäni kiinnostavasta aiheesta eli GeoGebran käytöstä yläkoulun geometriassa ja erityisesti monikulmioiden opiskelussa. Osana diplomityötäni kehitin valmiin tehtäväkokonaisuuden eli oppimisaihion GeoGebralla. Nyt tuo kokonaisuus on julkisesti kaikkien saatavilla GeoGebrassa osoitteessa https://ggbm.at/dgkmtmzb.

Taustaa

GeoGebra valikoitui tehtävien alustaksi siksi, että se on suunniteltu opetuskäyttöön, se on saatavilla suomeksi ja se on yksi matematiikan sähköisissä ylioppilaskirjoituksissa sallituista ohjelmistoista. Näin ollen GeoGebran käytön harjoittelu on perusteltua aloittaa jo yläkoulussa. GeoGebran käyttöliittymä on graafinen, jolloin se sopii erinomaisesti peruskouluikäisille oppilaille ensikosketukseksi matemaattisten ohjelmistojen maailmaan. Diplomityössäni kehitettyjen tehtävien tarkoituksena on auttaa oppilaita syventämään ymmärtämistään monikulmioista ja niiden ominaisuuksista. Monikulmiot ovat aiheena sellainen, joka sopii erityisen hyvin GeoGebralla toteutettavaksi.

Tein tehtävien kehittämisen kehittämistutkimuksena. Kehittämistutkimuksen tarkoituksena on yhdistää tieteellinen tutkimus ja käytännön opetustyö. Se koostuu useista toistuvista, lopullista tuotosta parantelevista kierroksista, jotka koostuvat ongelma-analyysistä, kehittämisprosessista ja arvioinnista. Ongelma-analyysissa kuvataan taustoja kehittämiselle, kehittämisprosessissa toteutetaan itse materiaalin kehittäminen ja arviointiosuudessa arvioidaan materiaalin toimivuutta todellisessa ympäristössä.

Tehtävien taustalla olevia näkökulmia olivat mm. hahmottava geometrian oppiminen, oppilaiden motivointi sekä tutkiva oppiminen. Kehittämisprosessissa loin itse tehtäväkokonaisuuden, joka koostuu 42 tehtäväsivusta GeoGebrassa. Kaikki tehtäväsivut on koottu GeoGebra-kirjaan, joka on osoitteessa https://ggbm.at/dgkmtmzb.

Tehtävien arviointi toteutettiin Ylöjärven Yhtenäiskoulussa yhdellä 7. luokalla ja yhdellä 8. luokalla. Oppilaat tekivät kuudella peräkkäisellä oppitunnilla kaikkia luomiani GeoGebra-tehtäviä, antoivat niistä palautetta ja vastasivat niihin liittyviin kyselyihin. Lisäksi kävin itse läpi oppilaiden vastaukset tehtäviin, jotta näkisin, ovatko he esimerkiksi ymmärtäneet tehtävänannot oikein. Arvioinnin tulosten perusteella parantelin tehtäviä ja julkaisin ne kaikkien saataville.

Tehtävät

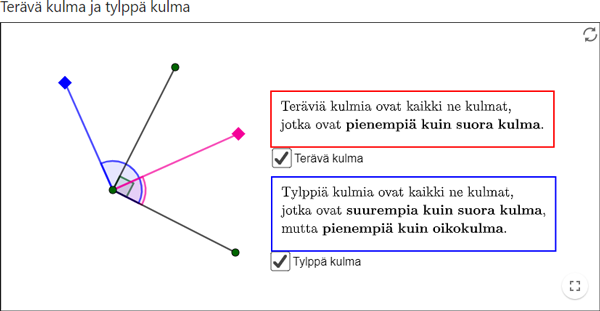
Tehtäväkokonaisuus eli oppimisaihio muodostaa loogisen kokonaisuuden, jossa tehtävien vaikeus vaihtelee, ja ohjeistuksen taso muuttuu alun yksityiskohtaisista ohjeista loppupään tehtävien suurpiirteisempään ohjeistukseen. Oppimisaihio koostuu kolmesta pääaiheesta: kulmat, kolmiot, nelikulmiot ja monikulmiot. Kulmiin liittyvissä tehtävissä kerrataan kulmiin liittyviä käsitteitä (esim. terävä ja tylppä kulma) sekä harjoitellaan kulmien piirtämistä GeoGebralla. Muita vaikeammat ja soveltavammat tehtävät on merkitty *-merkillä tehtävän nimen edessä. Yksi tähtitehtävä on Ylöjärven karttapohjalle asetettujen linkkimastojen kuuluvuusalueiden määrittely.

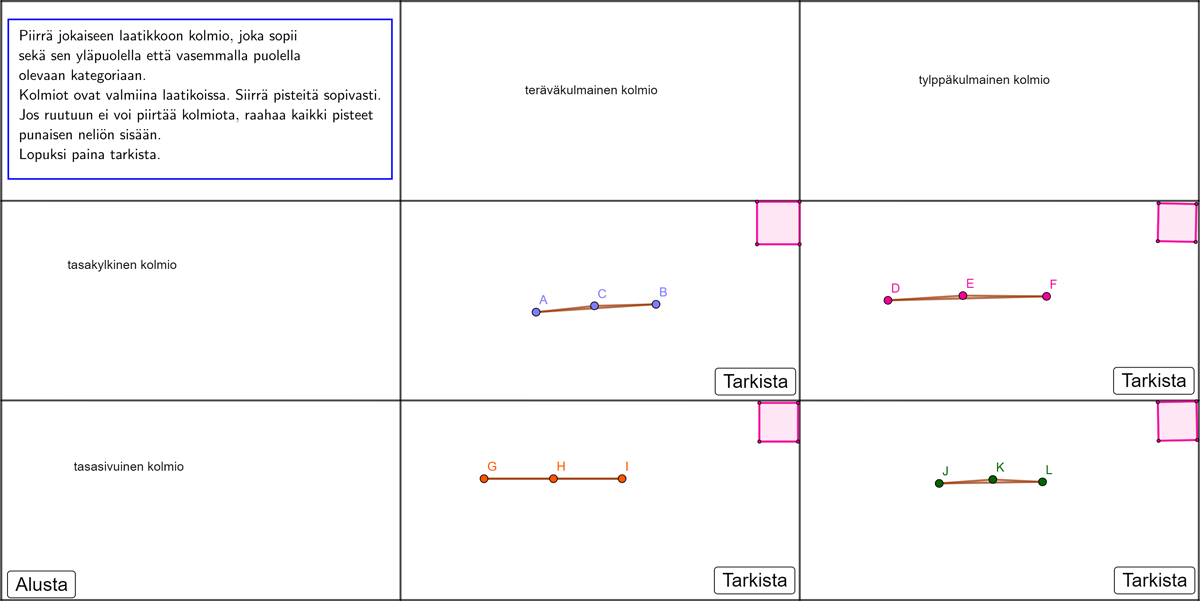
Kolmioihin liittyen harjoitellaan kolmioiden tunnistamista muista kuvioista, kolmion kulmien summaa sekä erilaisia kolmioihin liittyviä käsitteitä. Yleensä oppikirjoissa käsitellään tylppä- ja teräväkulmaisia kolmioita erikseen tasasivuisista ja tasakylkisistä kolmioista. GeoGebralla tein kuitenkin tehtävän, jossa näitä käsitteitä yhdistellään. Näiden lisäksi harjoitellaan tietysti GeoGebran käyttöä kolmioiden piirtämisessä, jolloin tutuiksi tulevat esimerkiksi tekstityökalu sekä liukusäädin. Soveltavina tähtitehtävinä ovat pohtia erilaisia tapoja piirtää tasasivuinen kolmio sekä tutustua Napoleonin lauseeseen.

Nelikulmioihin liittyvien käsitteiden harjoittelun jälkeen oppilaat pääsevät tutkivien tehtävien pariin. Oppilaiden tulee mm. piirtää nelikulmio, jonka toinen lävistäjä on nelikulmion ulkopuolella, jakaa neliöitä mahdollisimman monella eri tavalla kahteen osaan tai kolmeksi kolmioksi sekä tutkia, kuinka monta erikokoista neliötä voi piirtää 7×7-geolaudalle. Tehtävät ovat tähän asti olleet hahmottamista tukevia ja laskemista välttäviä, jolloin tehtävissä ei juurikaan ole ollut lukuarvoja. Nelikulmioihin liittyen on kuitenkin suorakulmion piirin suuruutta pohtiva tehtävä sekä puolisuunnikkaan pinta-alaan liittyvä tehtävä.

Viimeisessä kappaleessa oppilaat pohtivat aluksi monikulmion määritelmää ja ominaisuuksia (esim. Syntyykö aina pisteitä yhdistämällä monikulmio?) Lisäksi oppilaat harjoittelevat GeoGebran käyttämistä monikulmioiden piirtämisessä. Hyvä tapa integroida ohjelmoinnin opetusta geometrian opetukseen on käyttää GeoGebran ”kilpikonna-ohjelmointia”, jossa kilpikonna ohjelmoidaan piirtämään erilaisia kuvioita. Erilaisia kilpikonna-komentoja on vain kahdeksan, joten niiden avulla voidaan hyvin harjoitella ohjelmoinnin loogista puolta. Lisäksi kilpikonna-tehtävissä oppilaat oppivat mm. käyttämään GeoGebran painike-toimintoa.

Oppilaiden mielipiteitä

Tehtävien testauksessa oppilaat saivat antaa vapaasti palautetta tehtävistä ja lisäksi keräsin tietyistä tehtävistä tarkemman palautteen erillisillä kyselyillä. Oppilaiden GeoGebra-taitojen paraneminen oli näinkin lyhyessä ajassa selkeä. Ensimmäisten tehtävien kohdalla eniten toiveita tuli yksityiskohtaisemmista tehtävänannoista. Nämä toiveet vähenivät radikaalisti tehtävien loppua kohden. Oppilaat kommentoivat tehtäviin innoissaan onnistumisen kokemuksistaan. Lisäksi oppilaat innostuivat ongelmatehtävistä ja jäivät kärsivällisesti pohtimaan niitä itsekseen tai pienissä ryhmissä. Harvinaisen usein luokassa kuuluva puhe liittyi vain käsillä olevaan tehtävään.

• ”Tehtävä oli vähän epäselvä”
• ”en tajunnu toisen tehtävän tehtävänantoja, mutta oli se ihan kivaa”
• ”Ei kai me vielä jouduta lopettamaan!”
• ”Haluan [tehdä samantyyppisen ongelmatehtävän toisesta aiheesta], koska nämä tehtävät ovat oikeasti kiinnostavia.”
• ”Oli hämmästyttävää nähdä, miten erilaisia tehtäviä GeoGebralla pystyy tekemään ja miten helppoa niitä on tehdä kotona ja koulussa.”
• ”Jee, osasin!”

Ohjeet materiaalin käyttöön

Opettaja voi helposti antaa oppilaille tiettyjä GeoGebra-tehtäviä tehtäväksi sekä tutustua oppilaiden tuottamiin vastauksiin käyttämällä GeoGebran Ryhmät-toimintoa. Ohjeita Ryhmien käyttämiseksi löytyy sekä MAOL:n sivuilta (https://peda.net/yhdistykset/maol-ry/materiaalit/geogebra) että hakemalla GeoGebran ohjeista. Lisäksi MAOL:n sivuilta löytyy oppilaan ohjeet Ryhmään kirjautumiseksi ja tehtävien tekemiseksi.

Diplomityö löytyy kokonaisuudessaan osoitteesta: http://urn.fi/URN:NBN:fi:tty-201901031004.