Monikulmion neliöinti

Ympyrän neliöinti on yksi kolmesta suuresta klassisen ajan geometrisesta ongelmasta, joita ei voi ratkaista harpilla ja mitta-asteikottomalla viivaimella. Samanlaista mainetta eivät ole saavuttaneet ratkaistavissa olevat neliöintitehtävät, joissa saattaa kuitenkin olla pohtimista ihan kylliksi. Neliöinti tarkoittaa sitä, että on piirrettävä neliö, jolla on sama pinta-ala kuin annetulla kuviolla.

Yksinkertaisin tapaus on ehkä suorakulmion neliöinti. Se mielletään nykyisessä koulumatematiikassa ehkä mieluummin laskentatehtäväksi. Olkoot suorakulmion sivut a ja b. Merkitään etsittävän neliön sivua x:llä. Tällöin pitää olla

${x^2} = a \cdot b$,

josta

$x = \sqrt {a \cdot b} $.

Piirtämisen idea on selitetty Eukleideen Alkeiden kuudennen kirjan 13. lauseessa. Kalle Väisälän oppikirjassa Geometria se on lauseen 107 seurauksena 2: suorakulmaisessa kolmiossa hypotenuusaa vastaava korkeus on kateettien projektioiden keskiverto. Edellä oleva yhtälö voidaan nimittäin kirjoittaa verrannon

$\frac{a}{x} = \frac{x}{b}$

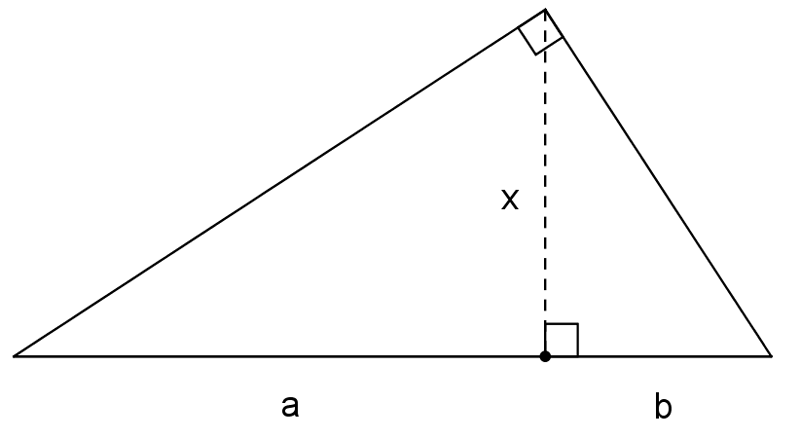
muotoon. Siitä käsitteen ”keskiverto” merkitys näkyy selvästi. Keskiverto on siis kahden suureen geometrinen keskiarvo. Piirtäminen perustuu Thaleen lauseeseen.

Suorakulmion neliöintiä tarvitaan välivaiheena kolmion neliöinnissä. Kolmio muunnetaan ensin samakantaiseksi ja sama-alaiseksi suorakulmioksi, joka sitten neliöidään (alla matletti, GeoGebra).

Monikulmio neliöidään muuntamalla se ensin sama-alaiseksi monikulmioksi, jossa on yksi kulma vähemmän, ja sitten vaiheittain samalla tavalla kolmioksi, joka lopulta neliöidään (alla matletti, GeoGebra).

Kuvioiden muuntamisen toisiksi sama-alaisiksi ei tarvitse rajoittua neliöintiin tai kolmiointiin. Esimerkiksi kolmio voidaan muuntaa samakantaiseksi ja sama-alaiseksi tasasivuiseksi puolisuunnikkaaksi (alla matletti, GeoGebra). Uuden näkökulman tähän tuo se, että nyt kanta ei määritä puolisuunnikkaan muotoa yksikäsitteisesti, vaan että tuloskuviossa on yksi vapaasti valittava jana (parametri): puolisuunnikkaan korkeus. Tästä seuraa lisäpohdiskelun aiheita, esimerkiksi kuinka suuri puolisuunnikkaan korkeus voi olla, kuinka suuria sen kulmat ovat, kuinka pitkä on toinen yhtä suurista sivuista. Piirtäminen perustuu kolmion ja puolisuunnikkaan pinta-alojen yhtäsuuruudesta saatavaan verrantoon

$\frac{{{s_x}}}{c} = \frac{{h – {h_x}}}{{{h_x}}}.$

Ympyrän neliöinnin mahdottomuus ei takaa sitä, etteikö kaarevareunaisia kuvioita voisi neliöidä. Laskemalla on helppo osoittaa, että jos esimerkiksi ympyrän säteiden suhde on $1:\sqrt 2 $ ja keskipisteiden välimatka on lyhyemmän säteen pituinen, niin kaarten rajoittaman ”kuunsirpin” (kaarikaksikulmio, engl. lune) pinta-ala on yhtä suuri kuin lyhyemmän säteen neliö (alla matletti, GeoGebra).

Aloituskuva: George Pagan III / Unsplash