Munuaiskartio ja muuta mukavaa
Koulumatematiikassa tutkitaan enimmäkseen yksinkertaisia peruskappaleita: palloja tai suoria lieriöitä tai kartioita. Syy on ehkä se, että niiden pinta-alojen ja tilavuuksien laskemiseen on tutut kaavat. Matematiikkaohjelmat antavat mahdollisuuden palata geometrian synteettisille juurille eli kuvioiden hahmottamiseen piirtämällä monissa sellaisissakin tapauksissa, joita ei koulukirjoissa käsitellä. Tarkastelen seuraavassa joitakin kartioita Geogebran avulla.
Vanhastaan koulumatematiikassa on käsitelty kartioista lähinnä pyramideja (särmäkartioita) ja suoria ympyräkartioita, joista saa koulumatematiikkaan sopivia laskuja. Opettajien käsitystä laskupainotteisuudesta kuvaa hyvin sosiaalisesta mediasta tavoittamani kommentti: ”Vino kartio ei liene aiheena kovin yleinen. Eipä siinä juuri muuta laskettavaa ole kuin tilavuus. Vaippa on kuitenkin niin eksoottinen pinta.”
Sama näkyy selvästi myös ylioppilaskirjoitusten matematiikan kokeiden tehtävistä. Niissä ei juuri vinoja kartioita ole ja nekin harvat lähinnä laskutehtävän viitekehyksenä eikä käsitteiden ymmärtämisen tai kartioiden geometristen ominaisuuksien takia. Nykyiset oppikirjat eivät kuitenkaan onneksi enää vieroksu vinojakaan kartioita käsitteen hahmottamisessa, missä voi ehkä nähdä dynaamisten matematiikkaohjelmien vaikutusta kirjantekijöiden ajatteluun ja mahdollisuuksiin tuottaa helposti havainnollisia kuvia.
Geogebrassa on valmis toiminto suoran kartion piirtämiseen, kun pohja tunnetaan objektina, esimerkiksi ympyrä tai ellipsi; lisäksi tarvitsee antaa vain korkeus. Kartion pohjakuvio voisi tietysti olla mikä tahansa muukin kuvio, esimerkiksi munuaiskäyrä (engl. nephroid [1]), mutta sellaista objektia Geogebraan ei voi luoda, koska käyrä piirretään implisiittisen funktion kuvaajana eikä geometrisena objektina. Valmis laajenna kartioksi -toiminto ei hyväksy funktiota lähtöarvoksi, joten munuaiskartio pitää hahmotella sivujanojen avulla (kuva 1).
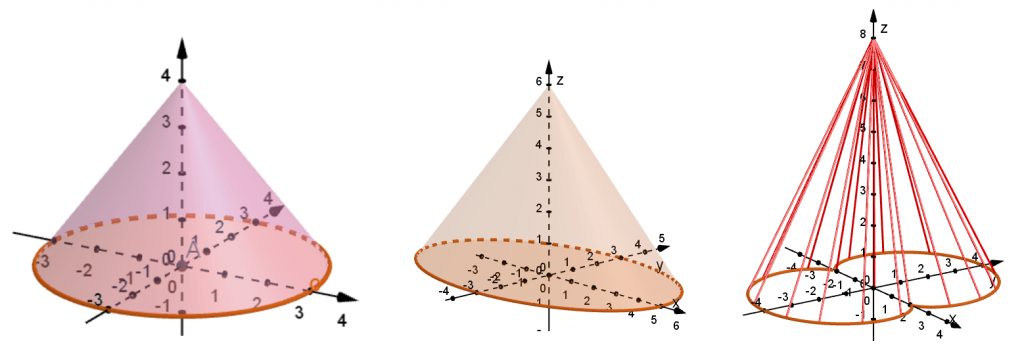
Valmista toimintoa ei ole myöskään vinojen kartioiden piirtämiseen. Suomalaisissa Geogebra-materiaaleissa on käsitelty vain vinoja särmäkartioita (pyramideja), mutta Geogebra-materiaaleissa on neljättäkymmentä vinoa ympyräkartiota (engl. oblique circular cone) käsittelevää työtä [2]. Nämä kaikki muodostetaan samalla idealla: huippupiste siirretään sivuun pohjan keskipisteen yläpuolelta (kuva 2). Pohja säilyy silloin muuttumatta ympyränä ja pohjan suuntaiset tasoleikkaukset ovat myös ympyröitä. Tähän perustuu se, että vinon ympyräkartion tilavuus on sama kuin suorankin.
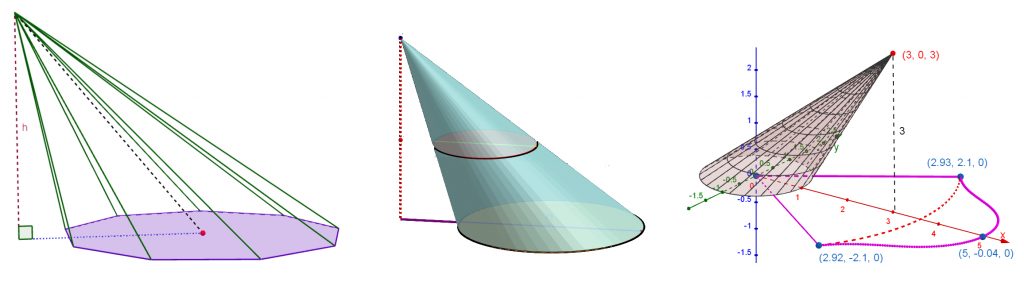
Nimitys ”vino ympyräkartio” on vakiintunut koulumatematiikassa tarkoittamaan vinoa ympyräpohjaista kartiota (kuva 3, vasen osakuva). Sitä nimitystä käytetään yleisesti niin meillä [3] kuin muuallakin [4]. Pieni sekaantumisen vaara on kuitenkin olemassa. ”Ympyräkartio” saattaisi näet viitata myös toisenlaiseen kappaleeseen (kuva 3, keskellä).
Kuvan 3 keskimmäisessä osakuvassa olevaa kartiota olisi luontevaa nimittää vinoksi ympyräkartioksi, jollei se nimitys olisi jo varattu vinolle ympyräpohjaiselle kartiolle (kuva 3, vasen osakuva) tai ainakin olisi harhauttavan lähellä sitä. Nimityksille voitaisiin hakea järjestelmällistä perustaa tarkastelemalla asiaa kartiopinnan määritelmästä lähtien: kartiopinta syntyy, kun kiinteän pisteen kautta kulkeva suora liikkuu avaruudessa itseään leikkaamatonta suljettua tasokäyrää pitkin (kuva 4). Tämähän on se tapa, jota käytettiin ainakin omana opiskeluaikanani aloitettaessa matematiikan opintoja yliopistossa [5]. Siihen näyttävät nykyään tukeutuvan myös lukion matematiikan oppikirjatkin [6].
Kartio on kappale, joka jää kartiopintaa leikkaavan tason ja kiinteän pisteen (huipun) väliin. Leikkaavasta tasosta kartiopinnan sisään jäävä osa on kartion pohja. Huipun ja leikkaavan tason väliin jäävä osa kartiopinnasta on kartion vaippa (engl. net). Kartion voitaisiin myös ajatella syntyvän siten, että janan toinen päätepiste on kiinteä ja toinen kulkee suljettua tasokäyrää pitkin [7].

Jos kartion määrittelevä tasokäyrä on ympyrä, jonka taso on kohtisuorassa kiinteän pisteen ja ympyrän keskipisteen kautta kulkevaa suoraa vastaan, niin kartiopinta on pyörähdyskartio (ympyräkartio). Kohtisuoralla tasolla leikkaamalla saadaan siitä suora ympyräkartio. Mikä olisi sitten sen kartion nimitys, joka saadaan pyörähdyskartiopinnasta akselia vastaan vinolla tasoleikkauksella (kuva 3, keskimmäinen osakuva)? ”Vino pyörähdyskartio” ei tunnu luontevalta, sillä kappale ei ole pyörähdyskappale niin kuin suora ympyräkartio on. Nimitys ”vino ympyräkartio” olisi muuten hyvä, mutta sitä käytetään usein vinosta ympyräpohjaisesta kartiosta niin kuin edellä jo todettiin.
Jos kartion pohja on ympyrä eikä huippu ole sen keskipisteen kautta kulkevalla kohtisuoralla suoralla, niin huipun ja pohjan keskipisteen yhdistysjanaa vastaan kohtisuora tasoleikkaus on ellipsi niin kuin edellä havaittiin (kuva 3, vasen). Vinoa ympyräpohjaista kartiota ei siis ole leikattu ympyräkartiopinnasta (pyörähdyskartiosta), vaan itse asiassa ellipsikartiosta! Silloin, kun halutaan olla ehdottoman varmoja tarkoitteesta, kuten esimerkiksi koetehtävässä, niin ei siis ehkä riitäkään pelkkä nimitys ”vino ympyräkartio”, vaan on tarpeen luonnehtia kappaletta tarkemmin, esimerkiksi juuri käyttämällä kuvaavaa nimitystä ”vino ympyräpohjainen kartio”.
Vastaavasti nimitys ”akseli” on hyvä varata vain pyörähdyskartiopinnasta leikatuille kappaleille ja puhua muuten huipun ja pohjan keskipisteen yhdistysjanasta, vaikka se tekstiä pidentäisikin. Ja tämäkin vain silloin, kun pohja on riittävän säännöllinen, jotta keskipisteestä puhuminen on järkevää, siis silloin kun pohja on symmetrinen pisteen suhteen. Tällöin ja vain tällöin on järkevää puhua myös kartion suoruudesta tai vinoudesta.
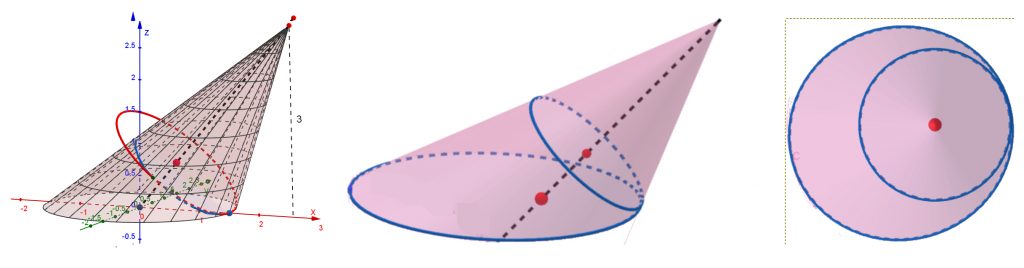
Palataan sitten munuaiskäyräpohjaiseen kartioon. Sen pohja täyttää edellä esitetyn symmetrisyysehdon, joten voidaan hyvin puhua suorasta ja vinosta munuaiskartiosta (kuva 5). Pyörähdyskartio se ei kuitenkaan ole, joten akselista puhuminen ei ehkä ole järkevää.

Tarkastellaan esimerkkinä erikoistapausta, jonka pohjakäyrän yhtälö on $$(x^{2}+y^{2}-4)^{3} = 108y^{2}$$
Olkoon kartion huippu pisteessä (6, 0, 8). Korkeus on silloin 8, pohjan piirin pituus 24 sekä x-akselilta lähtevät sivujanat $\sqrt{80}\approx 8,9$ ja $\sqrt{128}\approx 11,3$ (kuva 6).
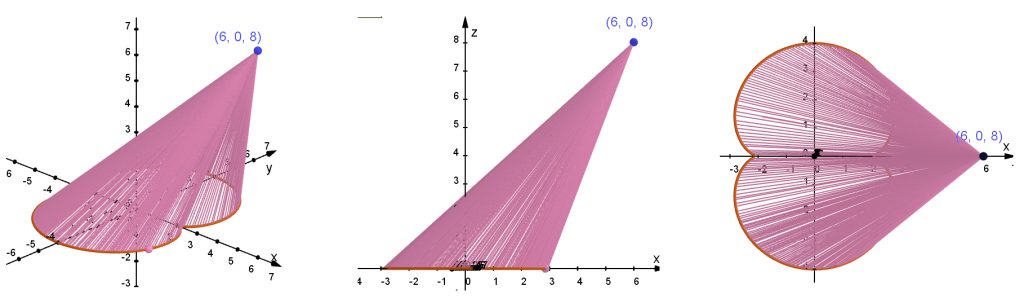
Alussa lainaamani opettajan mielestä kartion vaippa on eksoottinen pinta. Ehkä niin, mutta esimerkiksi munuaiskartion, jopa vinon munuaiskäyräpohjaisen kartion, vaippa on mahdollista levittää tasoon, koska kartio on viivoitinpinta. Tasoon levitettynä suoran ympyräkartion vaippa on ympyränsektori. Erään vinon ympyräpohjaisen kartion vaippa tasoon levitettynä on kuvassa 2 oikeanpuolimmaisena.
Eksoottisuusmielipidettä voisi perustella esimerkiksi sillä, että kuvan 6 munuaiskäyräpohjaisen kartion vaippaa ei oikeasti ole olemassa objektina Geogebra-piirroksessani, vaan se on piirretty sivujanan jäljen avulla. Siksi sitä ei voi levittää tasoonkaan sellaisenaan. Vaippaa voidaan kuitenkin approksimoida eli etsiä sille geometrinen likiarvo sellaisten kolmioiden avulla, joilla on yhteinen kärki kartion huipussa ja muut kärkipisteet kartion pohjan reunaviivalla (kuva 7, vasen osakuva)). Kolmiot voidaan sitten kääntää vaiheittain samaan tasoon ja lopuksi xy-tasoon. Tämä riittää tehdä vain toiselle puolelle, sillä tämän munuaiskäyränpohjaisen kartion vaippa on symmetrinen xz-tason suhteen.
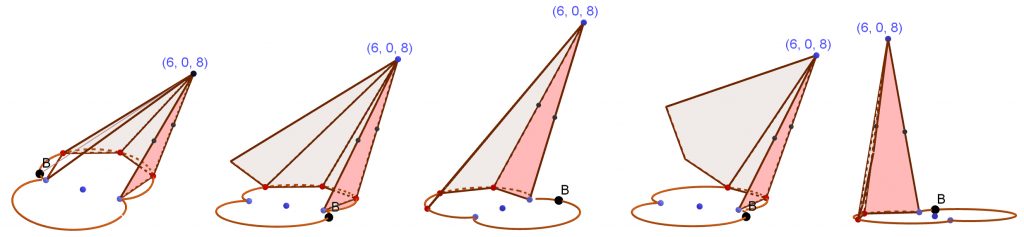
Käytännössä kohtasin teknisen ongelman. Kolme neljästä kolmiosta sain käännetyksi samaan tasoon. Sitten Geogebrani hyytyi eikä suostunut enää kääntämään kolmesta ensimmäisestä kolmiosta syntynyttä viisikulmiota (harmaa kuvassa 7, toinen osakuva oikealta) neljännen (punaisen) kolmion kanssa samaan tasoon. Periaate on kuitenkin selvä ja sama menettely toimisi paljon useammankin kuin kahdeksan kolmion approksimaation tapauksessa. Silloin ei kuitenkaan enää kannattaisi toimia vaihe kerrallaan, vaan kirjoittaa algoritmi. Sitä en ryhtynyt yrittämäänkään.
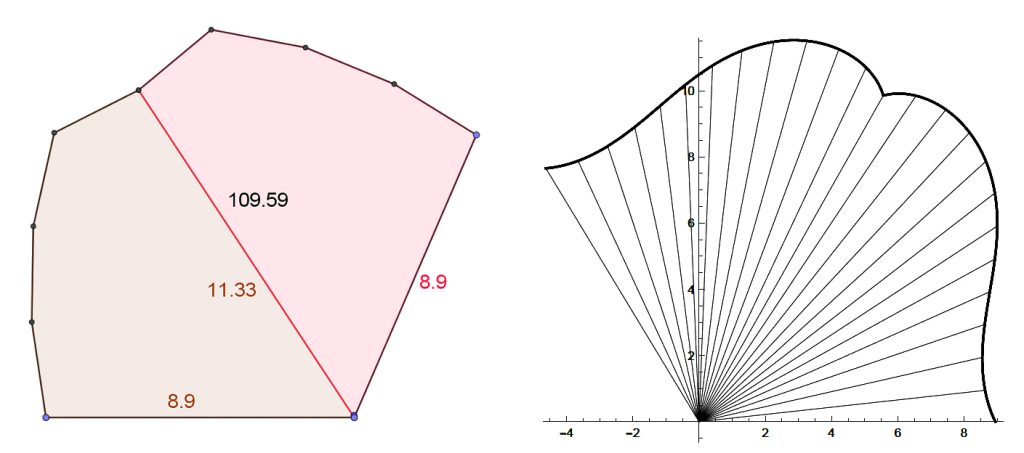
Matematiikan mahtavuus on siinä, että keinot eivät lopu siihen, että yksi työväline temppuilee. Vinon munuaiskartiomme vaippaa approksimoivat kolmiot voidaan piirtää mittojensa mukaan samaan tasoon sillä tavalla vierekkäin sijoitettuina kuin edellä kuvattu tasoonlevitysmenettelymme osoittaa (kuva 8, vasen).. Kuvio peilataan sitten punaisella merkityn janan suhteen, jolloin saadaan koko tasolevitys eli vaipan geometrinen likiarvo. Geogebra näyttää tällöin myös pinta-alan numeerisen likiarvon, noin 110. Tämä poikkeaa vain viitisen prosenttia pinta-alan oikeasta numeerisesta arvosta noin, 115. Oikeanpuoleisessa osakuvassa (kuva 8) vaippaa on approksimoitu 24 kolmiolla. Niiden janojen pituus, jotka on merkitty kuvaan, pysyy luonnollisesti samana kolmioiden määrän kasvaessakin.
Kiitän Simo Kivelää tämän artikkelin tekemisen aikana käydyistä keskusteluista, saamistani neuvoista ja kuvasta 8, Erkki Luoma-ahoa nykyisiä oppikirjoja koskevista tiedoista sekä Kaisa Vähähyyppää rohkaisusta.
Lähteitä ja lisää luettavaa
[1] Nephroid osoitteessa https://en.wikipedia.org/wiki/Nephroid
[2] Circular cones osoitteessa https://www.geogebra.org/search/circular%20cones
[3] Huusaari, Pekka: Kartio ja pyramidi osoitteessa https://peda.net/sievi/sievin-lukio/oppiaineet2/mp/maa32/tkapp/l4kjp, viitattu 21.1.2022.
[4] Roberts, Donna: Cones, MathBitsNotebook osoitteessa https://mathbitsnotebook.com/Geometry/3DShapes/3DCones.html
[5] Nyström, Evert Johannes: Korkeamman geometrian alkeet sovelluksineen. Otava, 1948.
[6] Esimerkiksi Hähkiönniemi, Markus ym: Juuri 3, sivu 159. Otava, 2021.
[7] Kivelä, Simo: M niin kuin matematiikka, s. 307. MFKA-Kustannus, 1998.
Tilaa Dimension uutiskirje – saat sähköpostiisi aina kuunvaihteessa koosteen tuoreimmista artikkeleista







