Olisiko metkasta matematiikasta harrastukseksi sinulle
Matematiikka ei ole vain vakavaa tiedettä ja teknistä laskentaa. Siitä on myös harrastukseksi ja aivoja virkistäväksi ajanvietteeksi maallikollekin. Tällainen metka matematiikka (engl. recreational mathematics) on Amerikan matemaattisen yhdistyksen luokituksessa yksi seitsemästätoista matematiikan osa-alueesta [1]. Yksinkertaisistenkin kuvioiden tai kuvaajien konstruointi hieroo älynystyröitä ja tuottaa parhaimmillaan myös esteettistä mielihyvää ainakin tekijälle itselleen.
Käytän tässä esimerkkinä GeoGebraa, koska se on kaikkien saatavissa ilmaiseksi verkosta sekä tietokoneelle että älypuhelimelle. Sitä voidaan siis käyttää sekä koulussa ja kotona että muutenkin vapaa-aikana. Siinä on mahdollisuus sekä ohjelmointiin että vapaaseen piirtämiseen. Valmiiksi ohjelmoitujen työkalujen – kuvioiden, funktioiden jne – ansiosta aloittelevakin harrastaja pääsee helposti alkuun ja saa tulosta vähällä vaivalla.
Kouluopetuksessa voisi ehkä olla hyväksi tuoda nykyistä enemmän esille matematiikan mahdollisuuksia elämyksellisyyteen ja oma-aloitteisuuteen ajattelun ja luovuuden kehittämisessä, vaikka ei koko ikäluokan osalta välttämättä niin vaativin tavoittein kuin STEAM-tyylisissä peli- tai robotiikkaprojekteissa [2]. Koulun merkitys matematiikan harrastamisen herättämisessä on kuitenkin suuri, sillä sellaista on vaikea ruveta harrastamaan, mitä ei tiedä olevan olemassakaan. Ja jos etsit aikuisiällä uutta älyllistä harrastusta, niin metka matematiikka voisi olla sellainen. Eikä sen tarvitse nykyään olla yksin puurtamista, sillä matematiikanharrastajien ryhmiä on paljon sekä Suomessa että kansainvälisesti monella verkkoalustalla.
Esimerkkikuvioita
Jo yksinkertaisista peruskuvioista voi saada aikaan monenlaista tekemistä ja pohtimista. Ensimmäisen esimerkkikuvion [3] pohjana (kuva 1) on vihreä neliö, sen päällä samankeskinen keltainen ympyrä ja edelleen punainen säännöllinen monikulmio. Tämä luodaan komennolla
Kuvio1(B, A, n)
missä A ja B ovat suoraan piirtoalueelle merkittävät yhden sivun päätepisteet ja n on kokonaislukuarvoja saava graafinen lukumuuttuja (liuku), jonka avulla valitaan sivujen lukumäärä. Monikulmion yhdelle sivulle piirretään tasasivuinen kolmio Kuvio2, jota kierretään yhteisen keskipisteen O ympäri tarpeeksi monta kertaa säännöllisen monikulmion jokaiselle sivulle:
Jono(Kierto(Kuvio2, t 360o / n, O), t, 1, n – 1)
Työskentely etenee komento kerrallaan niin kuin ohjelmoitaessa, vaikka mitään ohjelmaa ei kirjoitetakaan, vaan kunkin vaiheen toteutuksen onnistumisen näkee välittömästi.

Vastaavasti funktioiden kuvaajista voi saada kuvan, jota tarkastelemaan silmä pysähtyy, esimerkiksi antamalla funktion
y = a sin(bt)
parametreille a ja b erilaisia arvoja (kuva 2). On hyvä muistaa, että visuaalinen miellyttävyys, kauneus, on sanonnan mukaan katsojan silmässä. Joku voi nähdä siinä vain sekamelskaa ennen kuin alkaa hahmottaa säännöllisiä rakennepiirteitä. – Voisiko tällaisilla esityksillä olla vaikutusta koulumatematiikan tuottamien matematiikka-allergikkojen mielikuviin, jos ne auttavat unohtamaan matematiikan ja vain keskittymään katsomiseen (kuitenkin tietäen, että sen tekemisen takana on matemaattinen käsite)? Itse suunniteltu ja tehty kuvio vetoaa syvemmin tekijäänsä kuin paraskaan oppikirjatehtävä.
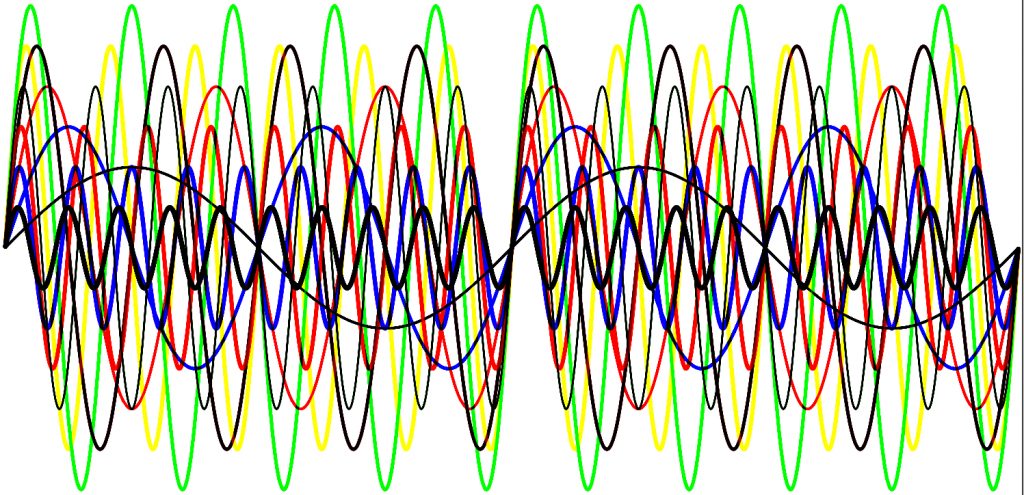
Matematiikan tekemisessä vain mielikuvitus on rajana. Käytin tätä parametrikäyrää (kuva 3) eDimension vuosikertakoosteen kansikuvana vuonna 2012 [4].

Parametrikäyrä taipuu myös ruusukuvioiden tuottamiseen (kuva 4), esimerkiksi
x = cos(nt) sin(t)
y = cos(nt) cos(t)
missä 0 ≤ t ≤ 2π ja n määrää terälehtien luvun.

Parametrikäyrillä voi piirtää kaikenlaista muutakin, esimerkiksi Albert Einsteinin kasvokuvan (kuva 5), vaikkakin työläästi, sillä muotokuvan sinifunktioista koostuvat koordinaattilausekkeet ovat kymmenien rivien pituisia [5].

Verkossa on paljon ruusukäyriä käsitteleviä sivustoja [6], [7]. Usein niiden piirtämiseen käytetään napakoordinaatteja. Arvelin ensin niiden menevän kaltaiseni kuvanharrastajamaallikon tarpeiden ja matemaattisen ymmärryksen yli. Mutta eipä vainkaan. Ruusukuvion piirtämisestä napakoordinaatistoon selvitään jopa edellistä yhtälöparia yksinkertaisemmalla koodilla. Tarvitaan vain kolme lukuparametria (liukua) a, p ja q ja yksi lauseke $r = a\ sin(\frac{p}{q} \alpha)$
Samasta lausekkeesta saadaan parametreja säätelemällä [8] mitä monimuotoisimpia käppyröitä (kuva 6).

Ideoinnilla ei ole tässäkään mitään rajaa. Voidaan lisätä yksityiskohtia, leikkiä dynaamisilla väreillä tai säätää parametreja (kuva 7). Terälehdet voidaan ”nyppiä” pois tarkasti yksitellen, kun kulmaparametrin animaatioaskel valitaan sopivasti, seitsenlehtisen ruusun tapauksessa 180o / 7 (kuva 7, oikeanpuoleinen osakuva). Reunakoristelut alkavat käyrällä olevasta pisteestä. Tiheys voidaan valita vapaasti sen animaatioaskeleella; suunta on kohtisuoraan käyrää vastaan, kun koristelujanan toinen päätepiste on käyrän tangentin normaalilla.

Geogebran komennoilla tai ohjelmointikielillä ohjelmoimalla saa toki hienoja kuvioita ja halutessaan niin monimutkaisia, että kukaan ei jaksaisi niitä piirtää eikä pystyisikään piirtämään samalla tarkkuudella. Se, mikä puuttuu, on vapaa leikki. Geogebrassa tämä voidaan toteuttaa yksinkertaisissa tapauksissa toiminnolla

tai raahaamalla pistettä piirtoalueella, kun jälki on valittuna objektin ominaisuuksista
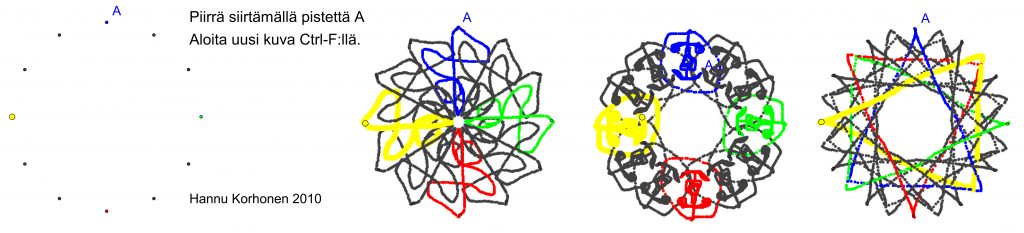
Monimutkaisemmasta piirroksesta on esimerkkinä kaksitoista samalle ympyrälle tasavälisesti aseteltua, toisistaan riippuvaa pistettä (kuva 8, vasen osakuva). Kaikki muut pisteet piirtävät saman kuvion samanaikaisesti, kun pistettä A siirretään [9]. Jotain kiehtovaa tässä leikissä täytyy olla, sillä esimerkiksi GeoGebran verkkomateriaaleissa on viidettä sataa kaleidoskoopin nimellä (kaleido, kaleidoskooppi, kaleidoskop, kaleidoscope, caleidoscope) kulkevaa, vastaavaan ideaan perustuvaa työtä.
Näistä pienistä kuvanpiirtoharjoituksista on vielä pitkä matka tietokoneen avulla tehtyyn digitaaliseen taiteeseen (engl. computer art, digital painting). Sitä tekevät ammattilaiset sekä itsensä taiteen vuoksi että monien alojen kuten mainonnan, julkaisemisen ja elokuvateollisuuden sovellusten takia. Kaupalliseen tuotantoon käytettävät ohjelmat ovat laajoja erikoisohjelmistoja. Silti edellä kuvatun kaltainen työskentely vaikkapa ilmaisella matematiikkaohjelmistolla antaa harrastajatekijälle mahdollisuuksia oman luovuutensa käyttämiseen ja kehittämiseen sekä tuottaa samantapaisia onnistumisen ja nauttimisen elämyksiä kuin ammattimainenkin taiteen tekeminen. Harrastaja ei tosin varmaankaan nimitä tuotoksiaan taiteeksi, mutta raja ei lopultakaan ole kovin jyrkkä, mitä osoittaa esimerkiksi New Yorkin Matematiikan kansallisen museon MoMathin – ei siis MoMA – järjestämä Geogebra-työpaja [10].
Lähteitä ja lisää luettavaa:
[1] Wikipedia-artikkeli Mathematical Association of America osoitteessa https://en.wikipedia.org/wiki/Mathematical_Association_of_America#Special_Interest_Groups
[2] Laakso, Noora: Uutta luova osaaminen yhteisöllisessä pelinkehitysprojektissa, Dimensio-lehti 9.8.2022, osoitteessa https://dimensiolehti.fi/uutta-luova-osaaminen-yhteisollisessa-pelinkehitysprojektissa/
[3] Geogebra-materiaali Säädettävä tähtimonikulmio osoitteessa https://www.geogebra.org/material/edit/id/qutd62fr
[4] EDimension vuosikertakooste 2012 saatavissa osoitteesta https://docplayer.fi/440774-Paakirjoitus-uskon-etta-taman-vuoden-2012-edimensio-on-vahintaan-yhta-hyva-tieto-ja-ideapankki-kuin-edeltajansa.html
[5] Wolfram Alpha: Second Einstein Curve osoitteessa https://www.wolframalpha.com/input/?i=2nd+einstein+curve
[6] Lee, Xah: Rose curve osoitteessa http://xahlee.info/SpecialPlaneCurves_dir/Rose_dir/rose.html
[7] Wolfram MathWorld: Rose Curve osoitteessa https://mathworld.wolfram.com/RoseCurve.html
[8] Geogebra-materiaali Rose curve (ruusukäyrä) osoitteessa https://www.geogebra.org/m/arntxcbv
[9] Geogebra-materiaali Kaleidoskooppi-12 osoitteessa https://www.geogebra.org/m/z9htcbpe
[10] National Museum of Mathematics osoitteessa https://momath.org/archived-events/events-2020/geogebra/







