Perushahmotusta neljännen ulottuvuuden mieltämiseen, osa4 – Neljännestä ulottuvuudesta kolmanteen: tesserakti

Opetus

15.4.2020

Tesserakti on neliulotteinen monitahokas. Sen voidaan ajatella syntyvän niin, että kuutiota siirretään oman särmänsä verran neljännen ulottuvuuden suuntaan. Se ei ole pelkästään matematiikkaa, vaan myös kuvataidetta, jopa mystiikkaa.

Tesserakti on kolmiulotteisen kuution neliulotteinen vastine, hyperkuutio. Sarjan ensimmäisessä osassa kerrottiin, että sen voidaan kuvitella syntyvän, kun kuutiota siirretään särmänsä mitta neljännen ulottuvuuden suuntaan kohtisuoraan edellisiä kolmea suuntaa vastaan [1]. Tesseraktia emme voi nähdä, mutta sen kaksi- tai kolmiulotteisen projektion kyllä.

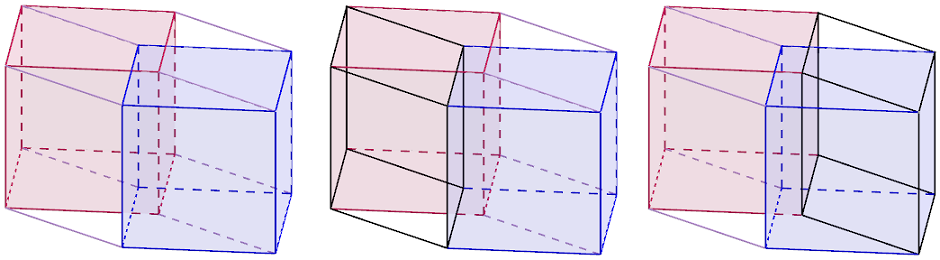
Hyperkuution kolmiulotteisen projektion kaksiulotteinen kuva. Siihen on väritetty kaksi hyperkuution kahdeksasta kuutionmuotoisesta solusta. Kuvasta voidaan hahmottaa muut kuusi solua yksi kerrallaan. Kahdessa muussa kuvassa on lihavoitu yhden tällaisen solun särmät.

Yhdensuuntaisprojektio on sillä tavalla havainnollisempi, että siitä näkyy selvästi tesseraktin rakentuminen siirryttäessä kolmesta ulottuvuudesta neljänteen. Keskusprojektiosta taas näkyy selvemmin tesseraktin rakenne. Pitää vain muistaa, että siinä näkyvät kuutiot ovat yhtä suuria, mutta kauimpana oleva näyttää pienemmältä perspektiivin takia. Muut solut, jotka myöskin ovat tietysti kuution muotoisia, näyttävät perspektiivikuvassa katkaistuilta pyramideilta.

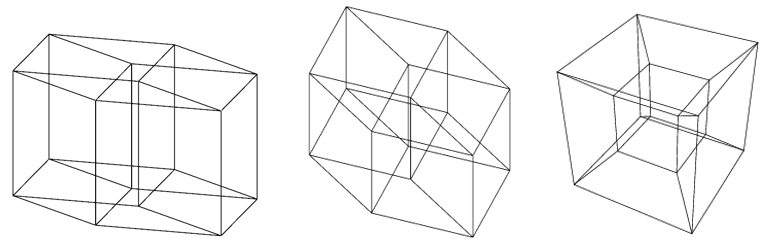
Tesseraktin projektio ilman perspektiiviä (kaksi yhdensuuntaisprojektiota eri suunnista [2], vasemmanpuoleiset kuvat) ja perspektiivin kanssa (keskusprojektio oikealla).

Tesseraktista on runsaasti materiaalia verkossa, havainnollista [3] ja matemaattisempaa [4]. Perusteellisesti projektioita ja niiden matematiikkaa selostetaan esimerkiksi tesseraktivideossa [5]. Monissa niistä käytetään keskusprojektiota, perspektiivikuvaa, ilman että sitä mainitaan erikseen.

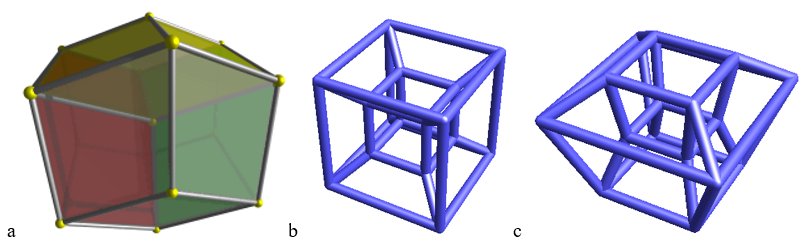
Kolme tesseraktin projectiokuvaa; a Wikimedia Commons, b ja c Wolfram Notebook [6].

Kolmiulotteisen kuution pinta (eli vaippa) muodostuu kuudesta kaksiulotteisesta neliöstä. Nämä rajoittavat avaruudesta kuution tilan pareittain kunkin ulottuvuuden suunnassa. Se voidaan levittää tasoon 11 tavalla. Hyperkuutiota rajoittavat vastaavasti kuutiot. Kun ulottuvuuksia on neljä, niin hyperkuution kolmiulotteinen ”pinta” muodostuu vastaavasti kahdeksasta kuutiosta, siis kaksi kutakin ulottuvuutta kohti. Levitys kolmeen ulottuvuuteen voidaan tehdä 261 tavalla [7].

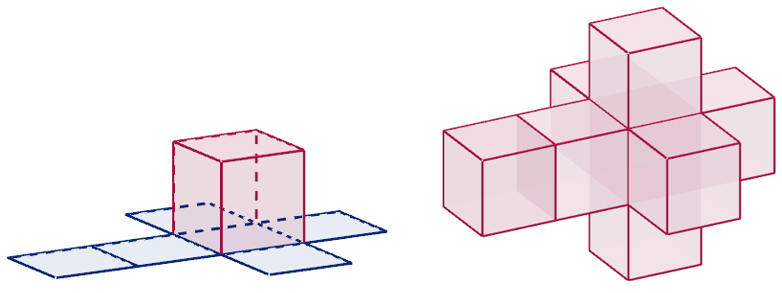
Kuutio ja sen vaippa levitettynä pohjatasoon (vasemmalla) ja hyperkuution ”vaippa” levitettynä kolmiulotteiseen avaruuteen /oikealla). Vastaavalla tavalla kuin kuution vaippa voidaan taivuttaa kolmannen ulottuvuuden suuntaan kuutioksi, voidaan hyperkuution ”vaippa” taivuttaa neljännen ulottuvuuden kautta hyperkuutioksi.

Tesseraktia ja sen varjoa on käytetty taiteessa monin tavoin. Myös kaupallista julistetaidetta on tarjolla. Tunnetuin maalaus on varmaankin Salvador Dalin maalaus Corpus hypercubus. Sen sijaintipaikka on Metropolitan Museum of Art New Yorkissa. Håkan Simbergin veistos Tesseraktin varjo on Kulosaaressa Helsingissä. Aihe on ollut esimerkiksi myös Vitalik Recordsin julkaiseman lp-levyn kannessa 1980-luvulla.