Sutinaa ja pöhinää jaksollisessa järjestelmässä I
Kemiassa tutustutaan jaksollisen järjestelmän systemaattiseen rakenteeseen ja niihin alkuaineatomien ominaisuuksiin, joihin järjestelmän tavallisin esitystapa perustuu.
Alkuaineita ei ole istutettu vakiintuneille paikoilleen mielivaltaisesti, vaan kunkin sijainnille on selkeät perusteensa. Pystysuunnassa olevien pääryhmien numero kertoo alkuaineatomin ulkoelektronien lukumäärän ja elektronikuorien lukumäärä kertoo mihin jaksoon eli vaakariviin kyseinen atomi kuuluu. Atomin viimeisenä täyttyvän alakuoren tunnus s, p, d, tai f kertoo, mihin lohkoon eli suorakaiteen muotoiseen alueeseen alkuaine järjestelmässä kuuluu. Tähän erinomaisen loogiseen järjestykseen ei tässä ole mitään huomautettavaa, mutta tämän selkeän ja virallisen rakenteen lisäksi voi jaksollisesta järjestelmästä löytää kohtalaisen paljon muutakin mielenkiintoista, sinällään ehkä aika pienimuotoista ja paikallista sutinaa ja pöhinää.
Iridium-sarja ja peilaavat parit
Jaksollista järjestelmää voi lukea monella eri tasolla, riippuen mitä alkuaineatomien ominaisuutta kulloinkin halutaan tarkastella. Ehkä yksinkertaisin tarkastelun taso lienee katsoa pelkästään alkuaineen järjestyslukua Z, joka kasvaa yksi kerrallaan vedystä eteenpäin: H (Z=1), He (Z=2), Li (Z=3), Be (Z=4), B (Z=5), C (Z=6), N (Z=7), O (Z=8), F (Z=9), Ne (Z=10) ja niin edelleen. Näin jaksollisen järjestelmän jokainen ruutu saa oman yksinkertaisen kokonaislukunsa väliltä 1–118, jossa viimeisellä paikalla on 2016 virallisen nimensä saanut alkuaine oganesson (Og).
Luovasti harhaileva mieli saattaa tällaisesta kokonaislukujen täyttämästä ruudukosta huomata muutaman kummallisen detaljin, vaikka nämä luvut eivät mitenkään edes liittyisi alkuaineisiin tai kemiaan. Jos tarkastellaan lukuja, jotka koostuvat kahdesta samasta numerosta, siis 11, 22, 33, 44, 55, 66, 77, 88, ja 99, niin huomataan, etteivät nämä luvut sijaitse täysin sattumanvaraisesti jaksollisessa järjestelmässä.
Erään koko maapallon kattavan satelliittipuhelinjärjestelmän aikoinaan kehittänyt yritys otti hankkeelleen nimen alkuaine iridiumista (77), koska järjestelmään kuului alun perin 77 pientä satelliittia. Lienee toisarvoista, oliko noiden satelliittien lopullinen lukumäärä todella 77 vai jotain muuta, sillä kyllähän iridium-puhelin nyt kuulostaa coolimmalta, kuin vaikkapa lantaani- tai ytterbium-puhelin. Jos siis iridium (77) kelpasi noinkin suureellisen hankkeen nimeksi, niin voitaneen lukusarjaa 11, 22, 33, 44, 55, 66, 77, 88, 99 tässä yksinkertaisesti kutsua ”iridium-sarjaksi”.
Monet iridium-sarjan luvut tykkäävät esiintyä jaksollisessa järjestelmässä diagonaalisesti pareittain: (44)–(77), (55)–(88), ja (66)–(99), joissa kaikissa lukujen erotus on sama 33. Yksinäisiltä susilta vaikuttavien ruutujen 11, 22, ja 33 sijainnit ovat myös hieman tarkemmin katsottuna kohtalaisen mielenkiintoisia. Jos tarkastellaan p-lohkon ”aktiivisen rungon” (siis ilman jalokaasuja ja alinta, vain keinotekoisia alkuaineita sisältävää 7. jaksoa) muodostamaa aluetta, niin arseeni (33) sijaitsee tämän 5×5 neliön keskellä.
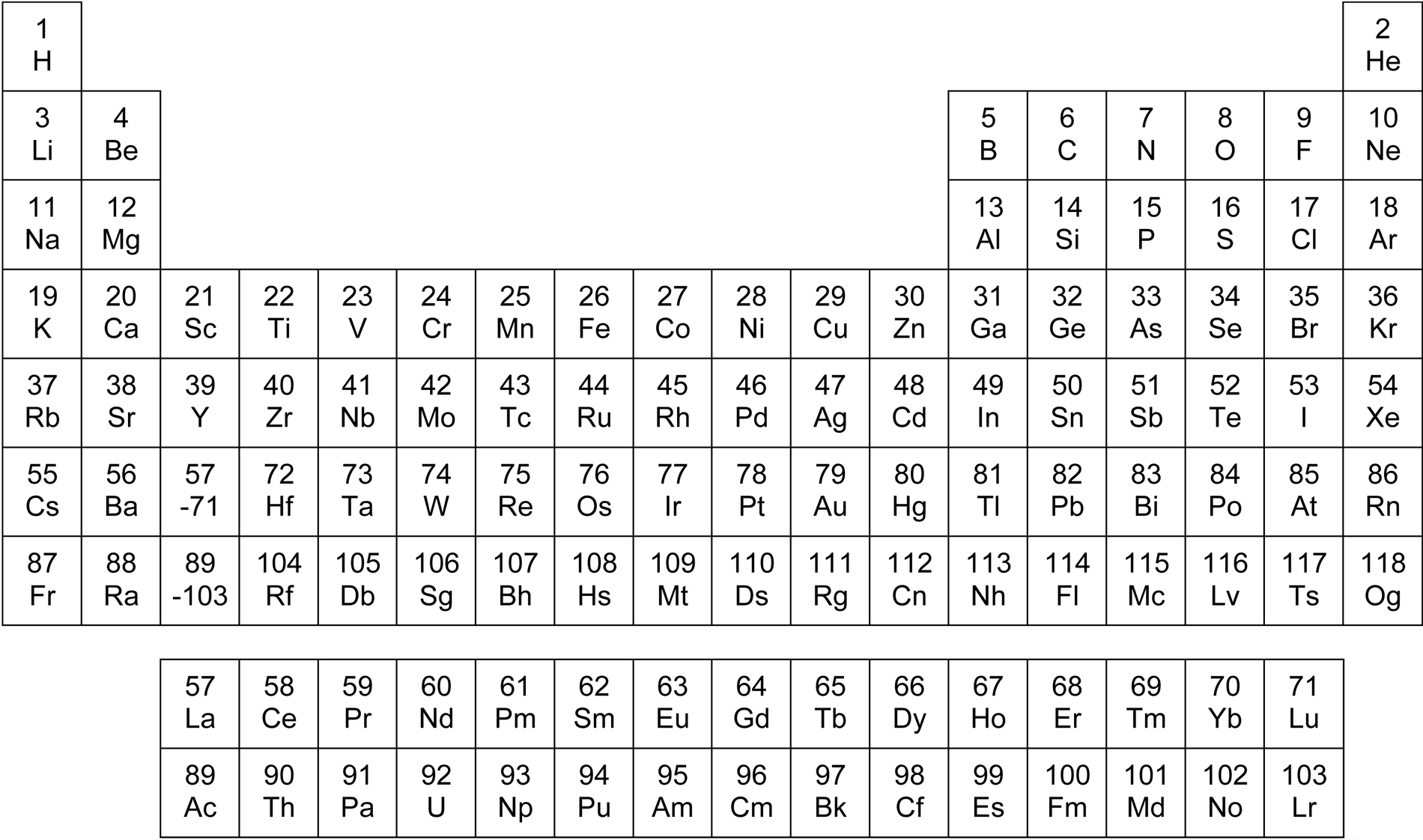
Arseenin ylä- ja alapuolella on ”peilaava” lukupari (15)–(51) ja 5×5 neliön reunoilla peilaavat lukuparit (13)–(31) ja (35)–(53). Näiden parien väliin jäävät parit (14)–(32) ja (34)–(52), jotka eivät sellaisenaan peilaa, mutta ovat ”peilaten” sukua d-lohkon pareille (23)–(41) ja (25)–(43), joiden välistä löytyy hyvin peilaava lukupari (24)–(42). Lohkojen s ja d rajalla on diagonaalisesti peilaava lukupari (12)–(21), jonka sivuilta löytyvät iridium-sarjastamme toistaiseksi puuttunut lukupari (11)–(22). Jos iridium-sarjan ajatellaan muodostuvan kaavalla n11, niin 99:n jälkeen tuleva jäsen ei ole 111, vaan 10×11=110, joka sijaitsee lukuparin (44)–(77) välittömänä jatkeena.
Diagonaalitukia ja tinatuoppeja
Tässä vaiheessa lienee paikallaan kysyä retorisesti ”No entä sitten?” No sitä sitten, että ainakin itse olen huomannut, etteivät jaksollisen järjestelmän alkuaineiden sijainnit, nimet, järjestysnumerot tai elektronegatiivisuusarvot, hapetusluvuista ja moolimassoista nyt puhumattakaan uppoa mitenkään helposti ainakaan omaan päähäni. Luonteva vasta-argumentti tähän on tietenkin ”Eihän näitä ole tarkoituskaan opetella ulkoa, nämä kaikki löytyy MAOL:n taulukoista”. Ei ehkä ole tarkoitus, eikä ehkä ole edes tarkoituksenmukaistakaan opetella tällaisia liikaa ulkoa, mutta aivan kuten ainoastaan vaaka- ja pystysuuntaisista palkeista koostuva rakennelma tarvitsee joitakin diagonaalitukia pysyäkseen varmemmin pystyssä, niin myös jaksollisen järjestelmän vaaka- ja pystysuuntaiset ominaisuudet oppii varmemmin, jos niiden väliin pystyy mielessään kiinnittämään edes joitakin ”diagonaalitukia”.
Esimerkiksi, jos muistaa ulkoa, että tuon p-lohkon ”aktiivisen” 5×5 neliön keskellä on luku (33), niin siitä on jo aika helppo hahmottaa, mitä järjestyslukuja tuon ”keskusneliön” ympäriltä löytää. Myös nuo peilaavat lukuparit auttavat ainakin itseäni hahmottamaan joissain jaksollisen järjestelmän kohdissa nopeammin, mitä järjestyslukuja päällekkäisillä aineilla on. Esimerkiksi, jos onnistuu mielessään sijoittamaan paikalleen luvun (13), niin voi olla helppoa muistaa, että sen alla on peilaava lukupari (31).
Lohkon d äärimmäisen oikeassa laidassa ovat sinkki (30) ja elohopea (80). Nämä muodostavat melkein säännöllisen kolmion p-lohkon tinan (50) kanssa ja kymmenykset vielä summautuvat sopivasti: 30 + 50 = 80. Nuori ihminen tuskin pystyy kuvittelemaan mitään tylsempää, kuin jonkun sukulaisen 50-vuotisjuhlat. Kysymys: mikä on tylsin mahdollinen 50-vuotislahja, minkä ihminen voi saada? Vastaus: tina (50) tuoppi. Näin esimerkiksi alkuaine tinaan saadaan sen järjestysluku (50) ”juotettua kiinni” enemmän tai vähemmän pysyvästi. Lyijy (82) olisi aivan väärä vastaus, koska lyijy on kaikkea muuta kuin tylsä; sehän on niin symbolinen ja runollinen alkuaine lyijynharmaine pilvineen, lyijynraskaine tunnelmineen jne. Käkikello on myös väärä vastaus, sillä 50-vuotislahjana siihen sentään sisältyy jonkinlaista latteaa huumoria, eikä sitä tietääkseni ainakaan vielä ole sitovasti osoitettu alkuaineeksi (Kk?). Toisaalta, en kyllä tiedä mitä 30-vuotias sitten tekisi sinkillä (30) tai 80-vuotias elohopealla (80), mutta ei nyt jäädä kompastelemaan lillukan varsiin tai menee vielä tarinalta loputkin uskottavuudesta.
Ainakin itse olen uteliaisuutta ja mielikuvitustani käyttäen saanut jaksollisesta järjestelmästä irti kohtalaisen paljon hupia ja hyötyä. Huomattavasti laajempi temmellyskenttä tietenkin aukeaa, kun pelkkien järjestyslukujen lisäksi tarkasteluun otetaan alkuaineiden nimet, elektronegatiivisuusarvot ja hapetusluvut. Näistä lisää osassa II.
Lue myös kirjoittajan aikaisempi kirjoitus Aminoffit ja Möttöset (22.10.2019)
Aloituskuva: isak55 / Shutterstock.com







