Teknologiatuettu yhtälön ratkaisemisen ymmärtävä oppiminen

Uusien oppimisteknologioiden suosio on nousussa digitalisoituvan yhteiskunnan myötä. Samaan aikaan esillä on huoli siitä, että oppilaiden oppimisen kannalta teknologian käytöstä voi olla enemmän haittaa kuin hyötyä. Tässä artikkelissa käytän väitöstutkimustani (Lehtonen, 2022) esimerkkinä, kuinka oppimisteknologia voi tukea oppilaiden matematiikan ymmärtävää oppimista.

Johdanto

Perinteinen koulumatematiikka painottaa tyypillisesti oppilaiden proseduraalisen sujuvuuden kehittämistä. Useimmiten sääntöjä opitaan ulkoa ja niitä sovelletaan mekaanisesti ilman ymmärrystä. Kuitenkin on todettu, että matemaattisten käsitteiden, operaatioiden ja relaatioiden ymmärtäminen (ns. käsitteellinen ymmärtäminen) on yksi tärkeimmistä matemaattisista taidoista (mm. Kilpatrick ym., 2001; Moschkovich, 2015). Käsitteellinen ymmärtäminen tukee oppilaiden matematiikan oppimisen sujuvuutta ja opitun muistissa säilyttämistä, ehkäisee virheiden tekemistä sekä auttaa uusien asioiden oppimisessa (Hiebert & Carpenter, 1992; Kilpatrick ym., 2001). Monet maat Suomi mukaan lukien ovatkin uudistaneet matematiikan opetussuunnitelmiaan painottamaan käsitteellistä ymmärtämistä (esim. Opetushallitus, 2014). Lisäksi näissä opetussuunnitelmissa korostetaan myös teknologian tärkeää roolia matematiikan luokissa.

Yhtälönratkaisu

Valitsin ensimmäisen asteen yhtälön ratkaisemisen oppimisen väitöstutkimukseni oppimisteknologian kehittämiskohteena monista syistä. Yhtälö on osa algebraa, jota tarvitaan matematiikan jatko-opinnoissa, luonnontieteiden sovelluksissa, monissa ammateissa sekä arkipäivän ongelmanratkaisussa. Siirtymä aritmetiikasta algebraan on kuitenkin haastavaa monille oppilaille. Tällöin oppilaiden on siirryttävä konkreettisista laskuoperaatioista (esim. 1+2=3) abstraktimpaan algebralliseen ajatteluun (esim. a+b=c), joka vaatii, muun muassa matemaattisten suhteiden sekä niiden edustamien kirjaimien ja symbolien ymmärrystä. Koulussa yhtälön ratkaisemisessa usein keskitytään sääntöihin ja mekaanisiin menetelmiin niihin johtavien käsitteiden ymmärryksen sijaan. Vaikka sillä tavalla saadaan kätevästi oikea ratkaisu, yhtälön ratkaiseminen ilman ymmärrystä, on kestävän oppimisen kannalta sudenkuoppa, sillä pinnallisten sääntöjen ulkoa muistaminen usein aiheuttaa sääntöjen unohtamista, virhekäsityksiä ja väärin soveltamista (Kilpatrick ym., 2001; Watson, 2009).

Yksi yleisimmistä opetetuista ratkaisumenetelmistä on käänteislaskutoimitus, jossa yhtälössä termin saa siirtää yhtäsuuruusmerkin toiselle puolelle, kun samalla vaihtaa sen laskutoimituksen käänteiseksi. Kuitenkin oppilas tyypillisesti oppii ulkoa, että siirrettäessä termin yhtälön toiselle puolelle sen etumerkki vaihtuu, ja käyttää sitä rutiinimaisesti, mikä yleensä toimii hyvin yhteen- ja vähennyslaskuyhtälöissä, esimerkiksi:

$$x+2=6$$ $$x=6-2$$ $$x=4$$

Jos oppilas ei ymmärrä, miksi kyseinen ratkaisumenetelmä pätee, hän helposti tekee virheitä ratkaistessa kerto- ja jakolaskuyhtälöitä, esimerkiksi:

$$2x=6$$ $$x=6-2$$ $$x=4$$ tai $$2x=6$$ $$x=\frac{6}{-2}$$ $$x=-3$$

Jotta oppilaat menestyisivät yhtälönratkaisussa, heidän tulee ensin ymmärtää perusteellisesti siihen liittyviä käsitteitä, kuten yhtälö, yhtäsuuruus ja yhtälössä olevia termejä: tuntematon, vakio ja kerroin (mm. Booth ym., 2014; Knuth et al., 2006). Yhtälönratkaisun käsitteiden ymmärtäminen kantaa pidemmälle, sillä se auttaa oppilaita muistamaan sääntöjä paremmin ja välttämään virhekäsityksiä sekä on pohjana haastavampienkin yhtälöiden ratkaisemiselle. Tutkimuksissa on osoitettu, että konkretia, moniesitysmuodot ja sosiaalinen vuorovaikutus tukevat yhtälön ratkaisemisen ymmärtävää oppimista (mm. Otten ym., 2019; Watson, 2009).

Teknologinen oppimisväline yhtälön ratkaisemisen ymmärtävää oppimista varten

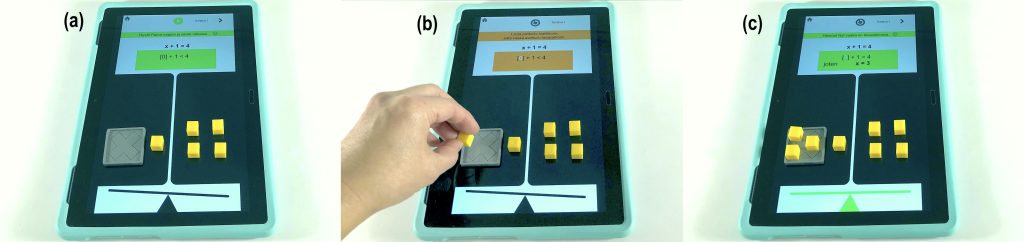
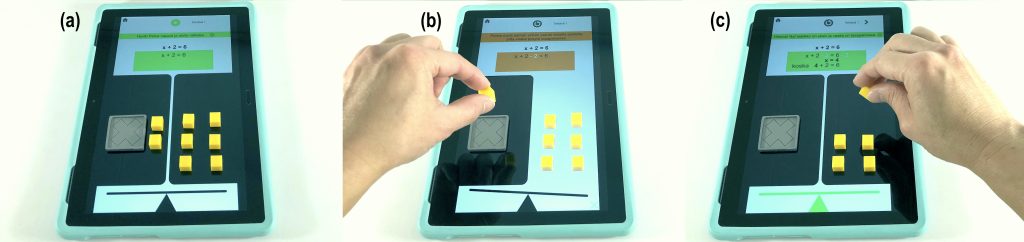
Kehitin yhteistyössä tietojenkäsittelytieteen opiskelijatiimin kanssa uudenlaisen oppimissovelluksen, joka konkretisoi yhtälön ratkaiseminen ja siihen liittyviä käsitteitä, esittää niitä eri muodoissa sekä tukee oppilaiden sosiaalista vuorovaikutusta. Kehitetty sovellus yhdistää fyysisten (perinteisten) ja digitaalisten välineiden vahvuudet: fyysisillä välineillä työskentely auttaa oppilasta keskittymään ja konkretisoimaan opittavia käsitteitä, kun taas digitaaliset välineet motivoivat häntä oppimaan ja antavat hänelle reaaliaikaista ohjausta ja palautetta. Yhtälö havainnollistetaan tabletin näytössä olevalla tasapainovaa’alla. Vaa’an kumpikin puoli edustaa yhtälön jompaakumpaa puolta. Vaa’alla olevat fyysiset esineet edustavat yhtälön lausekkeissa olevia termejä: kymmenjärjestelmävälineet (ykköskuutiot ja kymppisauvat) vakioita (ykkösiä ja kymmeniä) ja harmaat levyt tuntemattomia. Vaa’an tasapaino osoittaa, että yhtälön molemmat puolet ovat yhtä suuret. Oppilas ratkaisee yhtälöitä toiminallisesti liikuttamalla fyysisiä esineitä tabletin näytön painelun ja pyyhkäisyn sijaan, ja sovellus antaa oppilaan toiminnan mukaan ohjausta ja palautetta tekstinä, kuvina ja matematiikan symboleina.

Sovellus koostuu kahdesta tasosta yhtälön ratkaisemisen lähestymistapojen mukaan. Ensimmäinen taso suunniteltiin perusopetuksen opetussuunnitelman perusteiden (POPS, Opetushallitus, 2014) vuosiluokkien 3–6 matematiikan tavoitteiden mukaan. Oppilas tutustuu yhtälön (kaksi lauseketta, jotka on merkitetty yhtä suuriksi) ja tuntemattoman (yhtälössä luku, jonka arvo ei tiedetä) käsitteisiin. Sovelluksen avulla oppilas tutkii yhtälöä ja etsii yhtälönratkaisuja päättelemällä ja kokeilemalla, millä tuntemattoman luvun arvolla yhtälön molemmat puolet ovat yhtä suuret (kuva 1). Tämä taso kehittää oppilaan valmiutta laskutoimituksella yhtälön ratkaisemiseen.

Toinen taso suunniteltiin POPS:n (Opetushallitus, 2014) vuosiluokkien 7–9 matematiikan tavoitteiden mukaan. Oppilas ratkaisee yhtälöitä tekemällä saman laskutoimituksen yhtälön molemmille puolille niin kauan kunnes tuntematon jää yksin yhtälön toiselle puolelle (kuva 2). Vaa’an epätasapaino auttaa oppilasta muistamaan, että sama laskutoimitus tulee tehdä kummallekin puolelle, jotta yhtälön molempien lausekkeiden yhtäsuuruus säilyisi. Lisäksi tämä taso auttaa oppilasta ymmärtämään, että käänteislaskutoimitus-yhtälön ratkaiseminen perustuukin saman laskutoimituksen yhtälön molemmille puolille tekemiseen.

Interventio alakouluissa

Kehitettyä sovellusta kokeiltiin neljännessä ja viidennessä luokassa, joissa yhtälön ratkaisemista ei ole aikaisemmin opetettu. Yhden matematiikan oppitunnin aikana 12 neljäsluokkalaista opetteli ratkaisemaan yhtälöitä päättelemällä ja kokeilemalla, kun taas 12 viidesluokkalaista laskutoimituksella. Tunnin alussa luokanopettaja opetti oppilaille yhtälön ratkaisemiseen liittyvät käsitteet annettujen materiaalien avulla. Sitten opettajan johdolla oppilaat ratkaisivat pari yhtälöä yhdessä. Sen jälkeen neljäsluokkalaiset tekivät pareittain ensimmäisen tason harjoitustehtävät ja viidesluokkalaiset toisen tason harjoitustehtävät käyttämällä sovellusta. Kuten kuvassa 3 yhtälöitä ratkaistaessa oppilaita kannustettiin keskustelemaan tekemästään ja matemaattista ajatteluaan eli kielentämään (ks. Joutsenlahti & Rättyä, 2015). Kun oppilaspari oli ratkaissut yhtälön, jokainen kirjoitti yhtälönratkaisun ja ratkaisuprosessin omalle monisteelle tekstinä, kuvina ja/tai matematiikan symboleina.

Video 1. Oppilas ratkaisee yhtälön käyttämällä kehitettyä sovellusta ja kielentämällä (CC BY 4.0: Lehtonen ym., 2020).

Intervention aikana havainnoin oppilaiden parityöskentelyä. Intervention jälkeen mittasin oppilaiden yhtälön ratkaisemisen ymmärrystä ja osaamista kynä-paperi-testillä, jonka suoritti myös 35 seitsemäsluokkalaista, jotka olivat opiskelleet yhtälön ratkaisemista monia oppitunteja perinteisessä luokassa. Lisäksi haastattelin interventioon osallistuneita oppilaita ja luokanopettajia.

Tutkimustulokset osoittivat, että kehitetty sovellus tuki eri tasoisia matematiikan oppijoita eri tavoin. Yhtälön ratkaiseminen sovelluksella kavereiden kanssa motivoi oppilaita oppimaan yhtälön ratkaisemista. Oppilaat pitivät sitä hauskana ja nautittavana. Sovelluksella oppilaat voivat ratkaista yhtälöitä toiminnallisesti ja yhdistää yhtälön eri esitysmuotoja, mikä auttoi erityisesti keskitasoisia ja heikkoja oppilaita yhtälön ratkaisemisen keskeisten käsitteiden konkretisoimisessa. Parin kanssa oppilaat rakensivat yhtälön ratkaisemisen ymmärrystä konkreettisen sovelluksen, kielentämisen ja sosiaalisen vuorovaikutuksen avulla. Eräs heikko oppilas kertoi, että sovelluksen avulla yhtälön ratkaiseminen ei vaikuttanut niin abstraktilta ja toivoisi oppivansa muitakin matematiikan aiheita tällaisella sovelluksella. Lahjakkaat käyttivät sovellusta laskun ja ratkaisun tarkistamisvälineenä. Oppilaiden haastattelu ja testitulokset osoittivat, että interventio tuki heidän yhtälön ratkaisemisen ymmärrystään ja paransi oppimistulosta. Haastattelussa oppilaat ratkaisivat sovelluksella yhtälöitä onnistuneesti sekä pystyivät antamaan selkeän argumentin oman ratkaisuprosessin tueksi kuten videossa 1 (CC BY 4.0: Lehtonen ym., 2020). Kun interventioon osallistuneiden alakoululaisten testituloksia verrattiin seitsemäsluokkalaisten testituloksiin, oppilasryhmillä ei ollut merkittävää eroa.

Lopuksi

Edellä esitetyllä väitöstutkimukseni esimerkillä haluan osoittaa, kuinka oppimisteknologia voi tukea oppilaiden matematiikan ymmärtävää oppimista. Oppimisteknologia on kuitenkin vain työväline. Sitä tulee käyttää osana opetusta pedagogisesti (tässä tapauksessa kielentämisen ja sosiaalisen vuorovaikutuksen avulla) ja tarkoituksenmukaisesti eikä vain teknologian vuoksi. Toivon, että ulkoa opettelun sijaan artikkelini kannustaa opettajia tukemaan oppilaiden käsitteellistä ymmärtämistä oppimisteknologian avulla, sekä löytämään tätä tukevia menetelmiä ja oppimisteknologioita.

Väitöskirja on julkaistu sähköisesti ja se on ladattavissa osoitteesta https://urn.fi/URN:ISBN:978-952-03-2250-2

Muut lähteet

Booth, J. L., Barbieri, C., Eyer, F., & Paré-Blagoev, E. J. (2014). Persistent and pernicious errors in algebraic problem solving. Journal of Problem Solving, 7(1), Article 3.

Hiebert, J., & Carpenter, T. P. (1992). Learning and teaching with understanding. In D. A. Grouws (Ed.), Handbook of research on mathematics teaching and learning: A project of the National Council of Teachers of Mathematics (pp. 65–97). Information Age Publishing.

Joutsenlahti J., & Rättyä K. (2015). Kielentämisen käsite ainedidaktisissa tutkimuksissa. Teoksessa M. Kauppinen, M. Rautiainen & M. Tarnanen (toim.) Rajaton tulevaisuus: Kohti kokonaisvaltaista oppimista. Ainedidaktiikan symposium Jyväskylässä 13.–14.2.2014. Suomen ainedidaktisen tutkimusseuran julkaisuja 8, s. 45–62.

Kilpatrick, J., Swafford, J., & Findell, B. (toim.). (2001). Adding it up: Helping children learn mathematics. National Academy Press.

Knuth, E. J., Stephens, A. C., McNeil, N. M., & Alibali, M. W. (2006). Does understanding the equal sign matter? Evidence from solving equations. Journal for Research in Mathematics Education, 37(4), 297–312.

Lehtonen, D., Machado, L., Joutsenlahti, J., & Perkkilä, P. (2020). The potentials of tangible technologies for learning linear equations. Multimodal Technologies and Interaction, 4(4), Artikkeli 77. https://doi.org/10.3390/mti4040077

Moschkovich, J. N. (2015). Academic literacy in mathematics for English learners. Journal of Mathematical Behavior, 40, 43–62. https://doi.org/10.1016/j.jmathb.2015.01.005

Opetushallitus. (2014). Perusopetuksen opetussuunnitelman perusteet 2014. Suomen yliopistopaino.

Otten, M., Van den Heuvel-Panhuizen, M., & Veldhuis, M. (2019). The balance model for teaching linear equations: A systematic literature review. International Journal of STEM Education, 6, Article 30. https://doi.org/10.1186/s40594-019-0183-2

Watson, A. (2009). Algebraic reasoning. In T. Nunes, P. Bryant & A. Watson (Eds.), Key understandings in mathematics learning (Paper 6). Nuffield Foundation. https://www.nuffieldfoundation.org/project/key-understandings-in-mathematicslearning