Testin ja yo-tulosten välisestä yhteydestä
Voiko lyhyellä testillä ennustaa yo-arvosanaa? Neljännesvuosisadan kestäneen seurannan epätieteellinen tulos.
Helsingin teknillisen oppilaitoksen (nykyisin Metropolia Ammattikorkeakoulu) lehtori Pertti Toivonen kirjoitti Dimensiossa 5/1995 insinööriopiskelijoilleen tekemästään testistä, jossa opiskelijoiden piti ratkaista yksinkertaisia lukiomatematiikan tehtäviä: trigonometriaa, eksponentteja ja logaritmeja sekä algebrallisten lausekkeiden sievennyksiä. Ohessa testissä olleet 30 tehtävää. Toivonen hämmästeli, miten heikosti insinööreiksi opiskelevat osasivat asioita, joiden pitäisi hänen mielestään olla jokaisella insinöörinalulla tiedossaan.
Juttu innosti minut tekemään saman testin oman kouluni pitkän matematiikan abiturienteille. Halusin myös selvitellä, olisiko testin ja ylioppilaskirjoitusten pitkän matematiikan kokeessa menestymisen välillä jonkinlaista korrelaatiota. Kun aineistoa oli kertynyt viideltä vuodelta (1996–2000) ja tulokset olivat mielestäni hiukan kummallisia, kirjoitin aiheesta Dimensioon pienen jutun (Dimensio 3/2003). Näytti nimittäin siltä, että opiskelijat pärjäsivät yo-kokeessa sitä paremmin, mitä huonommin testi oli mennyt: kun testin keskiarvo oli matala, opiskelijoiden puoltoäänien keskiarvo oli korkea. Esitin jutussani selitykseksi sitä, että yo-kokeissa ei tuolloin tarvinnut osata edes perusasioita pärjätäkseen kirjoituksissa. Selitykselle ei tietenkään ole mitään perusteita.
Tuloksista oli siis luettavissa enteitä siitä, että testin ryhmäkohtaisilla keskiarvoilla tuskin on juuri mitään tekemistä ryhmän yo-menestyksen kanssa. Kuitenkin testin ja yo-menestyksen välillä näytti olevan melko voimakas positiivinen korrelaatio, kun tarkasteltiin yksittäisten opiskelijoiden suorituksia.
25 vuotta seurantaa
Saadakseni enemmän materiaalia jatkoin testin teettämistä. Nyt sitä on neljännesvuosisadan ajalta sisältäen lähes tuhannen opiskelijan tuotokset. Testi on pidetty kertauskurssin puolivälissä heti joululoman päätyttyä ensimmäisellä oppitunnilla, ja testi on tullut opiskelijoille ”yllätyksenä”. Siihen ei ole voinut valmistautua. Testissä kysyttävät asiat ovat sellaisia, että lukiolaisen kuuluisi tietää ne ilman erillistä ”pänttäämistäkin”. Koko aineisto on koottu taulukkoon 1, jonka vasemmassa sarakkeessa on testistä saatu pistemäärä ja näiden jakautuminen yo-arvosanoille näkyy merkintänä ”x”. Tässä taulukossa ei ole eritelty eri vuosien tuloksia.
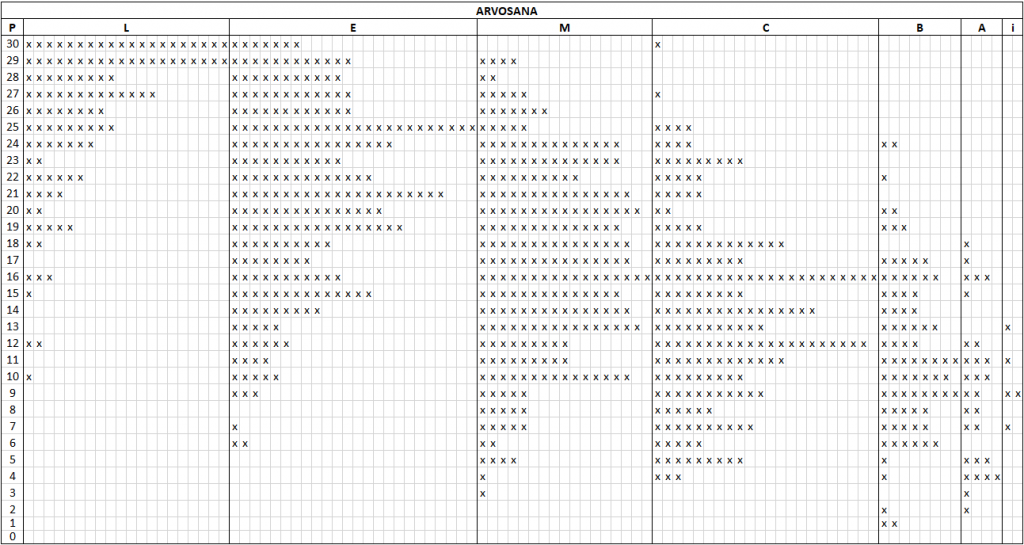
Yo-kirjoitusten arvosanojen suhteellisia osuuksia muutettiin vuodesta 2014 niin, että parhaimpien arvosanojen suhteellisia osuuksia kasvatettiin. Tämä aiheutti sen, että testin ja yo-arvosanojen vertailtavuus koko aineistossa kärsii. Koko aineistosta laskettava korrelaatiokertoimen arvo ei tällöin kuvaa testin ja yo-tulosten välistä yhteyttä asianmukaisesti. Olen siksi jakanut aineiston kahteen osaan ja tutkinut tilannetta ennen vuotta 2014 ja siitä eteenpäin. Molemmissa tapauksissa tulokset ovat kuitenkin samansuuntaisia. (Jonkinlaisella normittamisella olisi ehkä voinut saada tulokset vertailukelpoisiksi, mutta asia on sen verran mutkikas, että jätin sen tekemättä.)
Tuloksia
Tuloksissa on kaksi mielenkiintoista seikkaa. Ensinnäkin kunkin vuoden testikeskiarvon ja yo-tuloksen välinen korrelaatiokerroin on matala, eli tämä vahvisti aiemman päätelmän: testillä ei ole juurikaan ennustearvoa ryhmän yo-menestymiseen. Silmämääräisesti tämän voisi päätellä ehkä myös lopussa olevasta graafista. Tietysti jos tämä ”ryhmäkorrelaatiokerroin” laskettaisiin tarkoitushakuisesti vain joillekin vuosille, se toki saataisiin korkeammaksi.
Toinen, selvästi merkittävämpi tulos on, että yksittäisen opiskelijan testituloksen ja yo-kirjoitusarvosanan välillä on melko korkea korrelaatio. Ennen vuotta 2014 lasketussa aineistossa se on 0,65. Vuodesta 2014 vuoteen 2020 lasketussa aineistossa tämä on 0,67. Koko aineistossa luku on 0,62.
Kun olen kertonut opiskelijoille testin ja yo-kirjoitusten välisestä yhteydestä, he ovat yleensä olleet varsin innostuneita mahdollisuudesta ennustaa oma pitkän matematiikan yo-arvosanansa pelkän testin perusteella. Tietenkään kyseessä ei ole mikään lupaus yo-arvosanasta, mutta tässä pääsee puhumaan korrelaatiosta, selitysasteesta, regressiosuorasta ja syy-seuraussuhteesta luontevassa ympäristössä. Opiskelijat laskevat melkein pyytämättä odotusarvon yo-arvosanalleen, kun tietävät oman pistemääränsä.
Muitakin huomioita voi aineistosta tehdä. Silmäilemällä eri vuosien tehtäväkohtaisia keskiarvoja ehdollisen muotoilun värittämästä taulukosta (Taulukko 2), kiinnittyy huomio ehkä siihen, että trigonometrian kohdalla osaaminen on jossain määrin huonontunut ja algebran osaaminen on jokseenkin säilynyt samantasoisena kaikkina vuosina (vihreä – keltainen – punainen, vastaavuuksina: korkea – keskimääräinen – matala keskiarvo).
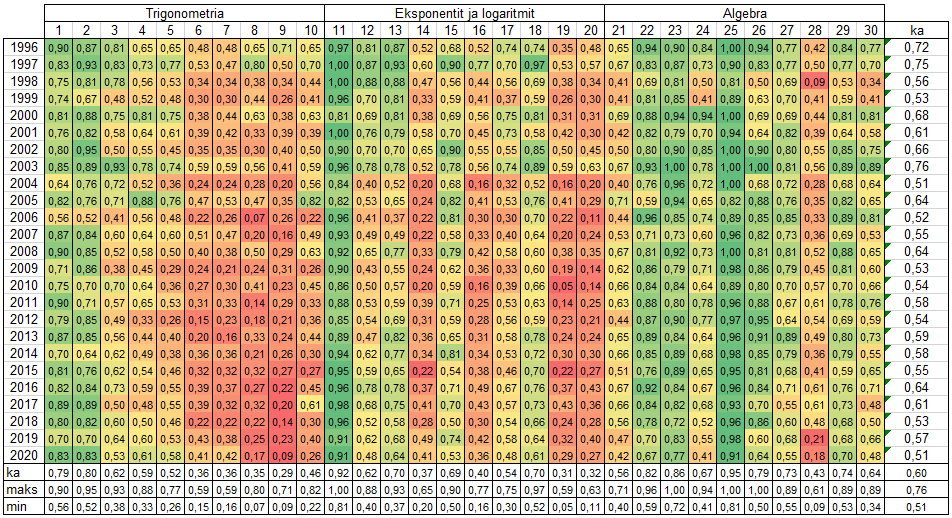
Testin keskiarvoja vertaamalla voisi ehkä sanoa osaamistason suunnan olevan laskeva (ks. Graafi). Yo-kokeen puoltoäänien keskiarvojen suunta näyttäisi viime vuosina taas olevan mieluumminkin nouseva. Tässä on kuitenkin otettava huomioon se, että yo-arvosanojen suhteellisia osuuksia muutettiin vuonna 2014. Paras selitys yo-arvosanojen nousulle lieneekin juuri tämä.
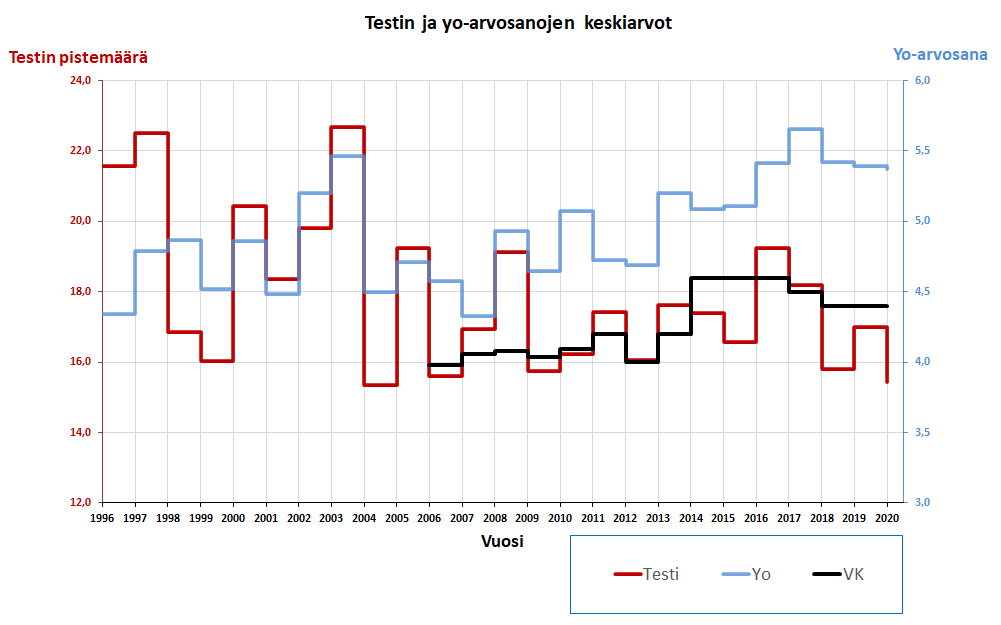
Graafissa on mukana puoltoäänien valtakunnalliset keskiarvot (VK) vuodesta 2006 alkaen. Tästä näkyy, että testiin osallistuneiden keskiarvot yo-kokeessa ovat koherenssissa valtakunnallisen keskiarvon muutoksen kanssa. En löytänyt tilastoja ennen vuotta 2006, mutta koska arvosanojen suhteelliset osuudet olivat pysyneet lähes samoina kaikkina näinä vuosina, voisi olettaa, että mitään suurta heittoa ei myöskään puoltoäänien keskiarvoissa noina vuosina ollut. Toisin sanoen graafissa olevan mustan käyrän voisi olettaa olevan suurin piirtein vakioitunut samalle tasolle kuin mitä se on vuosina 2006–2013.
Johtopäätöksiä
Vaikka kyseessä on näennäisesti pitkittäistutkimus (25 vuoden seuranta, n = 936), tuloksista ei ehkä pidä tehdä kovin yleistäviä johtopäätöksiä. Kyseessä on vain yhden koulun opiskelijat, joiden opettamiseen ovat osallistuneet useat opettajat. Tulosten yleistäminen edellyttäisi epäilemättä tieteellisempää otetta.
Kyllähän eri asioiden välille voi laskea korrelaatioita, mikäpä siinä. Voisi laskea esimerkiksi jonkin tietyn kurssin (tai preliminäärikokeen) arvosanan tai vaikkapa oppitunneilta poissaolojen määrän ja yo-kirjoitusten välisen korrelaation. Kyllä sieltä aina jokin luku saadaan. Kunhan mitattava suure valitaan sopivasti, voidaan korrelaatiokerroin yo-kirjoitusten ja tämän suureen välille saada huomattavankin korkeaksi.
Tekemäni testin tehtävät kuuluvat vain hyvin kapeaan osaan lukiomatematiikkaa ja kattavammin valituilla tehtävillä ja pienemälläkin määrällä kysymyksiä saataisiin epäilemättä korkeammat korrelaatiokertoimien arvot. Mutta minusta mielenkiintoista on, että erittäin suppea, triviaalitietoa mittaava ja nopeasti tehtävä testi antaa noinkin korkean korrelaatiokertoimen arvon.
Seuraavissa tehtävissä laskimen ja taulukoiden käyttö on kielletty.
TRIGONOMETRIA
- Kolmion kateetit ovat a ja b ja hypotenuusa on c. Jos kateetin a vastainen kulma on $\alpha $, niin tällöin ${\rm{sin\;}}\alpha = $
- Suorakulmaisen kolmion kateetit ovat a ja b ja hypotenuusa on c. Jos kateetin a vastainen kulma on $\alpha $, niin tällöin $\tan \alpha = $
- $\sin 0\;$=
- $\sin \pi \;$=
- $\cos \frac{\pi }{2} = \;$
- $\cos \pi = $
- $\sin \frac{{3\pi }}{2} = $
- ${ \sin ^3}x + \sin x{\cos ^2}x = $
- $\tan \frac{\pi }{{18}}\cot \frac{\pi }{{18}}$
- $\frac{{\sin x}}{{{{\cos }^2}x\;\tan x}} = $
EKSPONENTTI- JA LOGARITMIFUNKTIO
Sievennä lausekkeet tehtävissä 1 – 9.
- ${e^0}$
- $\ln 1$
- $\ln e$
- ${e^{\ln \left( {x + y} \right)}}\;$
- ${e^x}{e^{ – x}}$
- $\ln \frac{a}{b} + \ln \frac{b}{a}\;$
- $\ln {e^{{x^2}}}\;$
- ${e^{3x}} – 2{\left( {{e^x}} \right)^3}$
- $\ln \frac{{{x^2}y}}{{{z^3}}} – \ln \frac{{x{y^2}}}{z}\;$
- Jos $\ln (2x – 1) = 3$, niin tällöin $x = \;$
ALGEBRA
Sievennä seuraavat lausekkeet:
- $\frac{{{a^p}{{\left( {\frac{1}{b}} \right)}^q}}}{{{{\left( {\frac{1}{a}} \right)}^{ – 2p}}{b^{ – q}}}}$
- $\frac{{2x – 4y}}{{{{\left( {x – 2y} \right)}^2}}}$
- $\frac{1}{{ab\left( {\frac{1}{a} + \frac{1}{b}} \right)\;}}$
- ${x^3}{y^2} + {x^2}{y^3} – {x^2}{y^2}\left( {x – y} \right)$
- $\frac{{{a^2} + 2ab + {b^2}}}{{a + b}}\;$
- $\frac{{a – b}}{{{a^2} – {b^2}}}$
- $\frac{{1 – 2t}}{{1 – 4t + 4{t^2}}}$
- $1 – \frac{{{a^2} – {b^2}}}{{{a^2} + ab}}$
- $\frac{{\left( {x + 1} \right){\;^2} – 4x}}{{x – 1}}$
- $\frac{{{a^4} – {b^4}}}{{{a^2} – {b^2}}}$







