Välimerkkien matematiikkaa
Välimerkit helpottavat tekstin lukemista, sillä ne ilmaisevat virkkeiden ja niiden eri osien suhdetta toisiinsa. Kussakin kielessä on omat sääntönsä ja tapansa käyttää välimerkkejä. Sähköiset tietokannat antavat mahdollisuuksia laajojen aineistojen analysointiin. Matematiikka paljastaa kielestä riippumattomia säännönmukaisuuksia.
Puolalaisten tutkijoiden tekemässä tutkimuksessa [1] selvitettiin virkkeiden pituuksia seitsemässä eurooppalaisessa kielessä. Tuloksia kuvattiin riskifunktiolla. Se kertoo tietyn tapahtuman kumuloituvan todennäköisyyden ajan, matkan, toistotapahtumien määrän tms. funktiona, tässä tapauksessa siis todennäköisyyden, jolla suuri välimerkki ”.”, ”?” tai ”!” esiintyy tietyn sanamäärän jälkeen. Siten se kuvaa sanojen lukumäärällä mitatun virkkeen pituuden jakaumaa. Tulos osoittaa kielten suorastaan yllättävää samankaltaisuutta (kuva 1). Tutkimuksesta kertoi myös Phys.org News huhtikuussa 2023 [2].
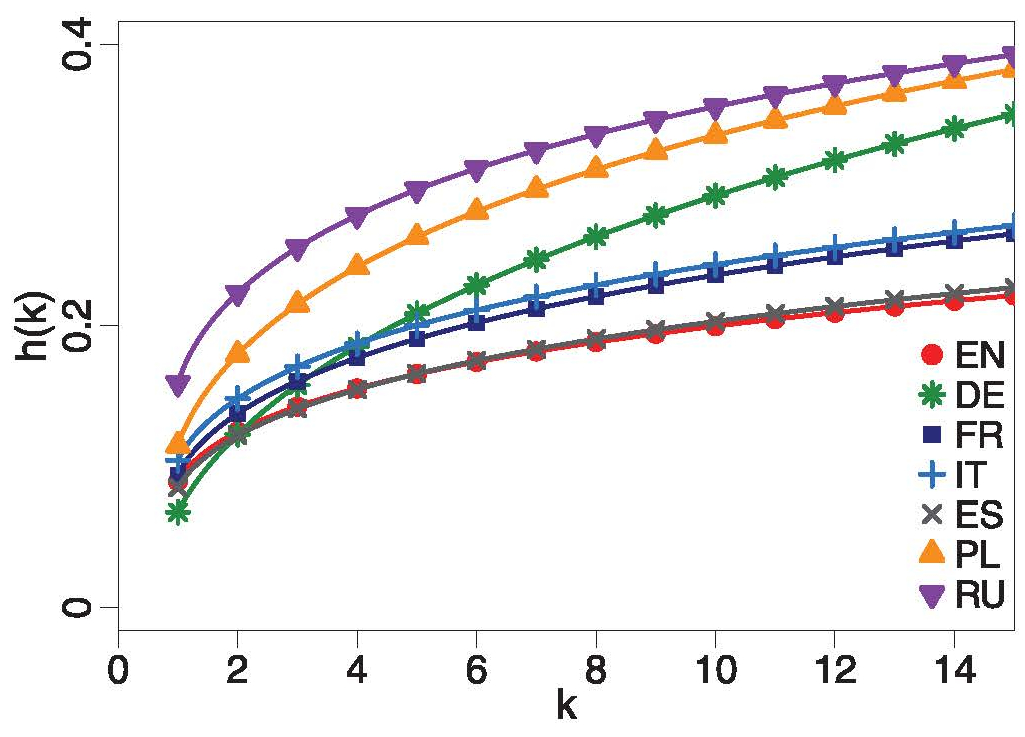
Jakaumat noudattavat karkeasti Weibullin jakaumaa, mutta ovat käytännössä vinoja ylöspäin, koska teksteissä saattaa esiintyä hyvinkin pitkiä virkkeitä. Siksi tutkijat käyttivät symmetrisen Weibullin jakauman kertymäfunktion asemesta kaksiparametrista riskifunktiota (engl. hazard function)
$$h(k)=1-(1-p)^{k^{\beta}-(k-1)^{\beta}}$$
(kuva 2). Se kuvaa siis ison välimerkin esiintymisen todennäköisyyttä sanojen määrällä mitatun tietynpituisen tekstijakson jälkeen [3].
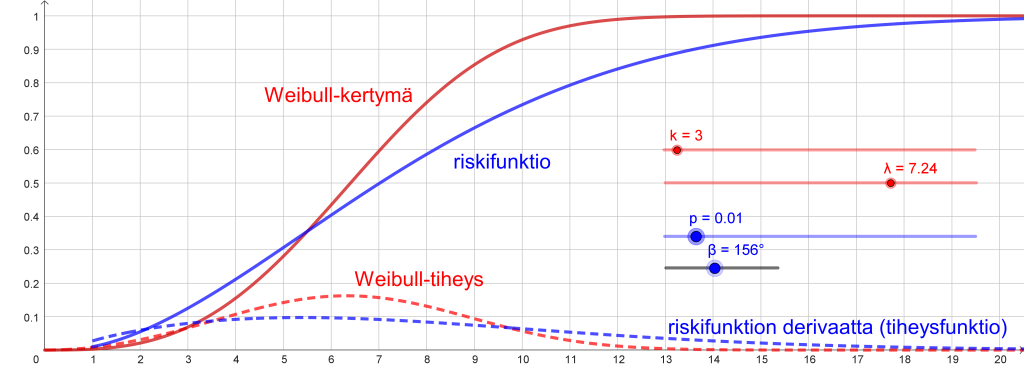
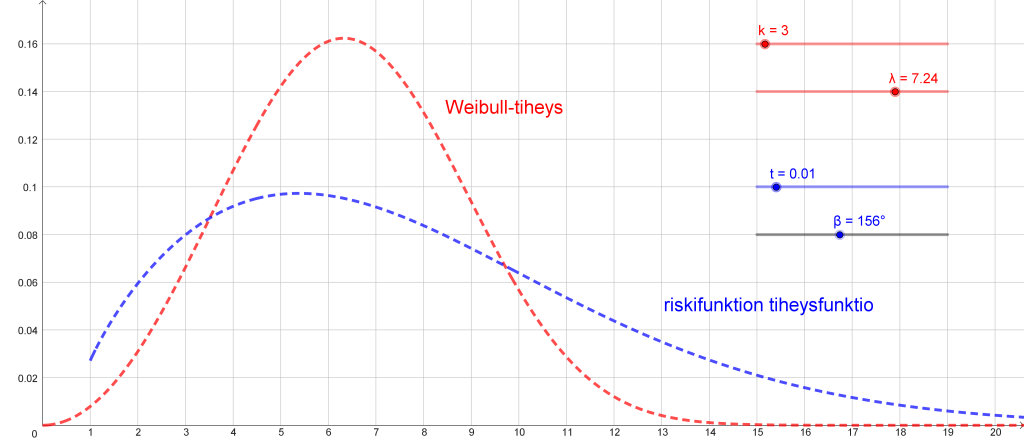
Artikkelissa [1] ei anneta parametrien kielikohtaisia arvoja, mutta ne on helppo selvittää likimäärin piirtämällä oikeanmuotoiset käyrät riskifunktion lauseketta käyttäen (kuva 3 ja taulukko 1).

Taulukko 1: Riskifunktion parametrien likimääräiset arvot kuvan 3 käyrien avulla määritettyinä
| Parametri | englanti | saksa | ranska | italia | espanja | puola | venäjä |
| p | 0,104 | 0,083 | 0,109 | 0,113 | 0,1005 | 0,132 | 0,169 |
| β | 1,344 | 1,458 | 1,284 | 1,280 | 1,260 | 1,344 | 1,276 |
Entä suomen kieli?
Suomen kielen virkkeiden pituuksista ei ole tehty puolalaistutkimusta vastaavaa vertailevaa todennäköisyysmallin mukaista tutkimusta Kotuksesta ja Kielipankista saamiemme tietojen mukaan. Suomen kielen rakennetta on muuten analysoitu paljonkin [4]. Virkkeet ovat lyhentyneet ajan mittaan, sillä esimerkiksi 1600-luvun saarnoissa oli 29,6 sanaa virkettä kohti, mutta nykyisessä yleiskielessä lähdeaineistosta riippuen 12,2 [5] tai 13,3 [6]. Laaja 21 miljoonan sanan Parole-tekstikorpus antaa vielä pienemmän lukeman: 11,1 sanaa virkettä kohti. Virkkeen pituus vaihtelee jonkin verran tekstilajeittain: sanomalehdet 11,2, tietokirjat 12,7 ja romaanit 9,8.
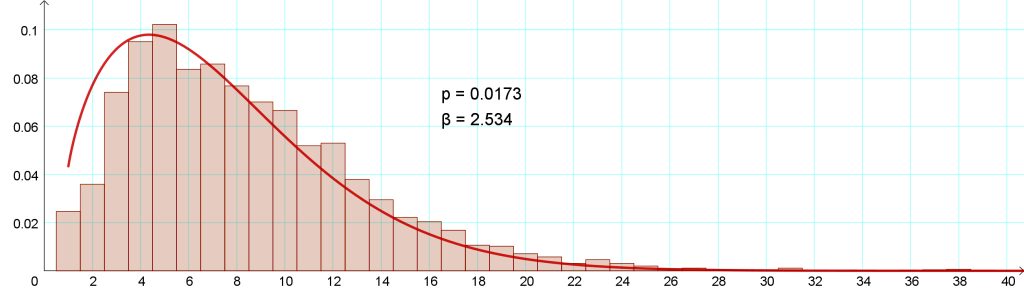
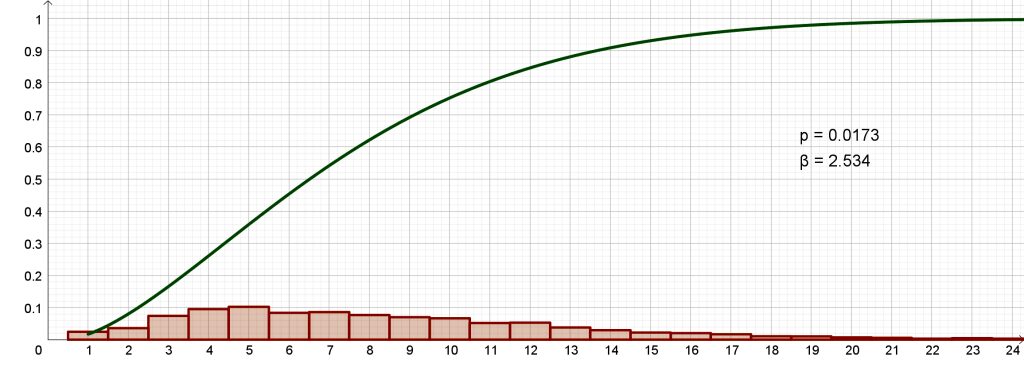
Halusimme kuitenkin kokeilla, millaisia tuloksia riskifunktio antaisi suomenkielisistä teksteistä. Tommi Kinnusen romaanin Pimeät kuut tekstissä on 38 120 sanaa ja 4 509 virkettä, pisimmässä virkkeessä 51 sanaa ja lyhimmissä vain 1, tyyppiarvo 5. Yhden sanan virkkeiksi analyysiohjelma on tulkinnut myös lyhenteitä ”y.” ja ”s.”, keskustelupuheenvuoroissa esiintyviä nimiä ”Pekka?” ja ”Pentti?” sekä päivämääriä ”1.8.” jms. Riskifunktio pystyy mallintamaan Pimeiden kuiden tekstiä kuitenkin erittäin tarkasti (kuva 4). Parametreiksi saadaan p ≈ 0,016 ja β ≈ 2,5.
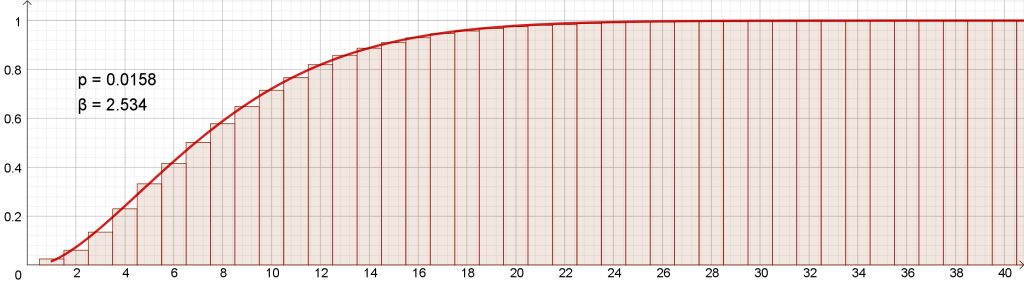
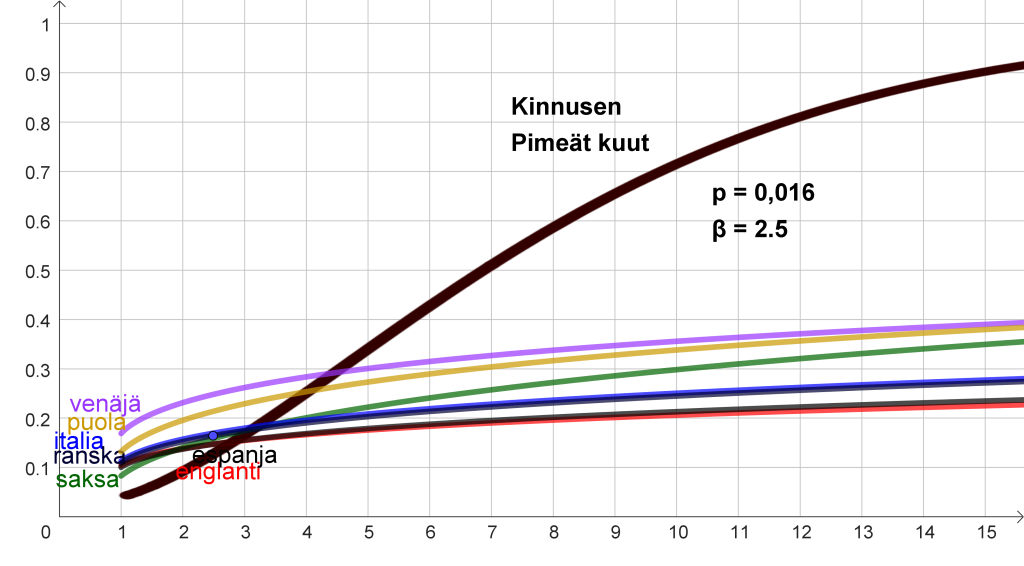
Kinnusen suomen kieli näyttäisi poikkeavan melkoisesti puolalaisten tutkijoiden analysoimista kielistä (kuva 5). Tässä ei ehkä ole mitään kummasteltavaa, sillä muista kielistä saadut tulokset perustuvat laajoihin, monenlaisia tekstejä sisältäviin kielikorpuksiin. Yleinen piirre on esimerkiksi se, että tieteellisten tekstien virkepituus on jopa kaksinkertainen normaalitekstiin verrattuna. Kinnusen tekstin keskimääräinen virkepituus 8,5 sanaa virkettä kohti on sen sijaan lyhempi kuin suomenkielisessä romaanikirjallisuudessa keskimäärin. Tämä selittänee esimerkiksi sen, että riskifunktio saavuttaa Kinnusen tekstissä 90 prosentin tason jo 15. sanan kohdalla, kun esimerkiksi englannissa päästään silloin vasta vähän yli 20 prosenttiin.
Aleksis Kiven Seitsemää veljestä lukiessa näyttäisi siltä, että puolalaisten tutkijoiden riskifunktio ei ehkä sopisi kovinkaan hyvin mallintamaan sitä, koska teksti koostuu tavallaan kahdesta toisiinsa lomittuvasta erilaisesta osasta: yhtäältä hyvin lyhyitä virkkeitä sisältävistä keskustelupuheenvuoroista ja toisaalta normaalista kertovasta proosatekstistä. Kirjan tekstissä on 81 246 sanaa ja 9 889 virkettä, pisin virke 64 sanaa, lyhin 1, joka on samalla tyyppiarvo.
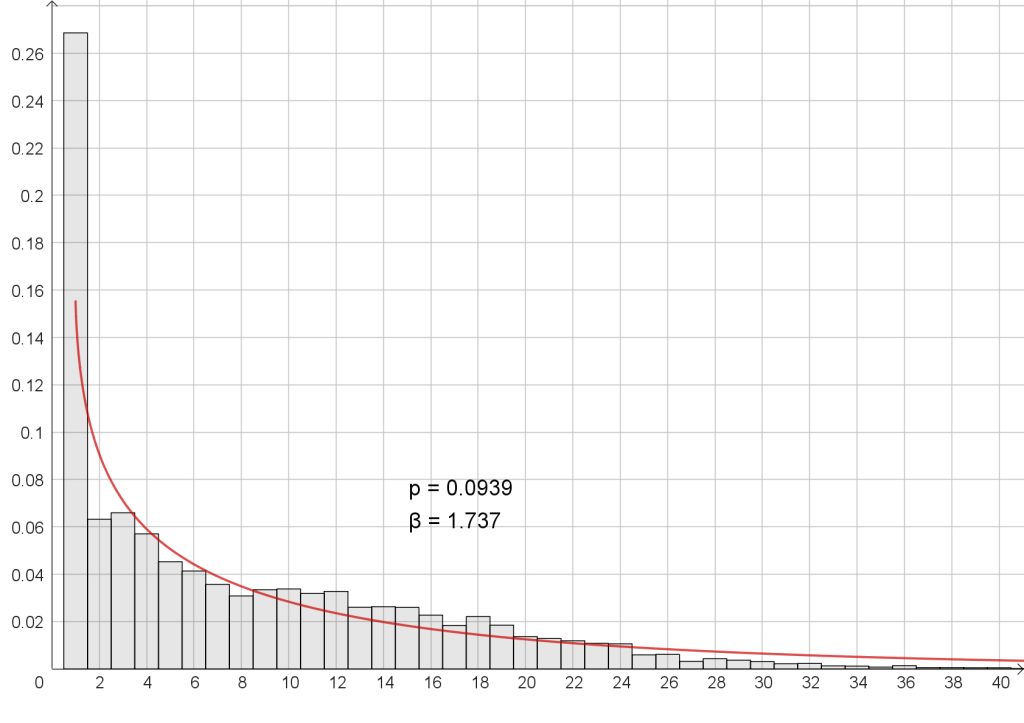
Lyhimpien virkkeiden (pituus = 1) osuus ylikorostuu myös siksi, että jokaisen keskustelupuheenvuoron alussa on puhujan nimi pisteellä erotettuna ”Jussi.”, ”Viertola.” tai ”Nimismies.”, jotka tulkitaan aina yhden sanan virkkeiksi. Keskustelupuheenvuoroissa on kyllä muutenkin runsaasti yhden sanan virkkeitä: ”Hm.”, ”Nyt.” tai ”Menepäs.”. Yhden sanan virkkeitä onkin enemmän kuin neljännes (kuva 6, ylempi).
Yllättäen parametrien arvot eivät kuitenkaan poikkea puolalaisten tutkijoiden analysoimien tekstien arvoista niin paljon kuin voisi luulla. Esimerkiksi p-parametri p ≈ 0,094 on englannin ja saksan arvojen välissä. Parametri β ≈ 1,74 on puolestaan vähän isompi kuin missään tutkitussa kielessä. Parametrien arvot riippuvat kuitenkin selvästi siitä, mihin jakauman kohtaan riskifunktio sovitetaan (kuva 6, alempi).
Seitsemän veljestä poikkeaa muista analysoimistamme romaaneista erityisesti p-parametrin osalta (taulukko 2). Se kertoo tiheysjakauman hajonnasta (varianssi, toinen keskusmomentti). Hajonta on sitä suurempi eli tiheysjakauma on sitä tasaisempi, mitä pienempi p on. Jakauman tasaantumisen seurauksena riskifunktion tiheysjakauman huippukohta (moodi, typpiarvo) luonnollisesti kasvaa eli siirtyy graafissa oikealle.
Parametri β taas puolestaan kertoo jakauman huipukkuudesta (neljäs keskusmomentti), joka on sitä suurempi, mitä suurempi β on. Suuret β:n arvot merkitsevät siis sitä, että jakauma keskittyy voimakkaasti, joten pitkiä virkkeitä on hyvin vähän.
Anni Swanin suomennoksen Liisa Ihmemaassa antamat parametrien arvot osoittavat, että kääntäjä on noudatellut hyvin uskollisesti Carrollin tekstiä virkkeiden pituudenkin osalta. Käännöksen ja alkuperäisteoksen parametrien arvot poikkeavat toisistaan vähemmän kuin muista kirjoista (taulukko 2), vaikka siis kyse on eri kielistä; toisistaan jopa vähemmän kuin voisi odottaa englannin kielen artikkelien ja prepositioiden lyhyyden perusteella.
Taulukko 2: Riskifunktion antamia parametrien arvoja
| Kirjoittaja | Teoksen nimi | p | β |
| Tommi Kinnunen | Pimeät kuut | 0,0173 | 2,534 |
| Aleksis Kivi | Seitsemän veljestä | 0,0939 | 1,737 |
| Lewis Carrol | Alice in Wonderland | 0,0323 | 2,043 |
| Anni Swan | Liisa Ihmemaassa | 0.0292 | 2,205 |
| Minna Canth | Kauppalopo | 0.033 | 2,434 |
| Ilmari Kianto | Punainen viiva | 0,038 | 2,187 |
Käyttämämme työvälineet
Tässä työssä pitäydyimme tutuissa ilmaisissa työvälineissä ja pienissä suomenkielisissä aineistoissa. Näkökulma on ollut enemmänkin tutustua välineiden mahdollisuuksiin kuin pyrkiä tieteellisesti merkittäviin kielen käytön analyyseihin. Pääasiallinen työnjako on ollut se, että Mikko on vastannut tekstien analysoinneista ja Hannu vertailuista puolalaisten tutkijoiden aineistoihin. Kielipankin Korp-aineisto [7] tarjoaisi vapaan mahdollisuuden laajempienkin kielikorpusten analysoimiseen, mutta se menee paljon yli tämän työn tavoitteiden.
Analyysi-idean pohjana on Python-koodi, joka tutki Seitsemän veljeksen sanojen pituuksia [8]. Vähän muokattuna se soveltuu hyvin myös virkkeenpituuksien analysoimiseen. Seitsemän veljeksen, Punaisen viivan, Kauppalopon ja Alice in Wonderlandin tekstit ovat peräisin Project Gutenbergin sivuilta [9]. Pyysimme Tommi Kinnuselta hänen kirjojensa tekstejä ja iloksemme hän antoikin käyttöömme useammankin kirjan. Valitsimme Pimeät kuut, sillä se kertoo opettajuudesta. Ennen analyysiä siivottiin pois ylimääräiset varsinaiseen kirjaan kuulumattomat tekstit, joita Project Gutenberg -kirjoissa on tiedostojen alussa ja lopussa kertomassa itse projektista.
Koska tutkimme virkkeiden pituuksia, niin laskettavat sanajaksot alkavat isoista välimerkeistä (.?!) ja päättyvät niihin. Pientä virhettä tuloksiin tulee esimerkiksi järjestysluvuista ja päivämäärämerkinnöistä, joita on Pimeissä kuissa aika paljon. Jätimme molemmissa kirjoissa mukaan lukujen nimet. Seitsemässä veljeksessä ne ovat lukuja ja Pimeissä kuissa kuukausien nimiä. Ne lisäävät lukujen ensimmäisten virkkeiden pituuksia, koska otsikot eivät pääty välimerkkiin.
Tekstistä poistettiin vielä ylimääräiset ”turhat” merkit kuten: (, ), ”, “, *, -, _, jne. Varsinkin välimerkkien jälkeiset merkit tyyliin “…lainaus päättyy!” ovat ongelmallisia laskennan kannalta, sillä koodi tutkii, onko sanan viimeinen merkki iso välimerkki. Edellisen virkkeen esimerkissä se on lainausmerkki ”. Muokatut tekstit muutettiin tekstitiedostoiksi Google Driveen. Niitä Python-koodi lukee.
Tämän jälkeen lasketaan virkkeiden pituudet eli isojen välimerkkien (.!?) välissä olevien sanojen määrä Pythonin sanakirjamuuttujaan (dictionary). Sanakirja järjestetään lukumäärän mukaan ja tulostetaan sarkainerotelluksi tekstitiedostoksi. Tätä tiedostoa voi sitten muokata vaikkapa GeoGebralla. Tarkempi selitys koodista löytyy blogista [10].
Jutun kuvat 2–7 on piirretty GeoGebralla. Se on matematiikan oppimiseen suunniteltu ilmainen työvälineympäristö. Monipuolisuutensa ansiosta se soveltuu erinomaisesti tulosten visualisointiin. Virkkeiden sanamäärien frekvenssitaulukot voidaan kopioida sellaisinaan GeoGebran laskentataulukkoon, laskea siellä suhteelliset frekvenssit ja viedä sarakkeet listoina histogrammin piirtämiskomentoihin yhdellä napinpainalluksella. GeoGebra muodostaa riskifunktiosta h(x) vastaavan tiheysfunktion h’(x) automaattisesti vain yhden pilkun lisäyksellä.
Riskifunktioiden sovittamista kertymä- ja todennäköisyystiheysjakaumiin helpottaa olennaisesti se, että parametrien arvoja voidaan muuttaa analogisesti graafisilla lukumuuttujilla, ns. liu’uilla (kuva 2). Lausekkeitakaan ei tarvitse kirjoittaa jokaiselle tekstille erikseen, vaan uudet funktiot saadaan nimeämällä funktio uudella nimellä ja antamalla uudet parametrien arvot. Koordinaatiston vapaa skaalattavuus ja kuvan koon jatkuva muuttaminen hiiren pyörällä osoittautuivat myös erittäin käyttökelpoisiksi toiminnoiksi.
Loppupohdiskelua
Todennäköisyysperustaisia kielimalleja voidaan käyttää puheentunnistuksessa, konekääntämisessä, kielen jäsentämisessä, tekstintunnistuksessa, tiedonhaussa ja keskustelevissa chatboteissa. Puolalaisten tutkijoiden käyttämä riskifunktio on äärimmäisen yksinkertainen esimerkki n–grammimalleista. Ne laskevat todennäköisyyksiä sille, mikä on n:s merkki tai sana edellisten n–1 merkin tai sanan jälkeen. Ne perustuvat siis tilastollisiin frekvensseihin eivätkä niinkään ilmausten kiinteyteen (idiomaattisuuteen) tai sanojen merkitysyhteyksiin [11].
Puolalaistutkimuksen riskifunktio ennustaa, millä todennäköisyydellä iso välimerkki (.?!) esiintyy tekstissä n‑1 sanan jälkeen riippumatta näiden sanoiksi tulkittujen merkkijonojen muodosta tai merkityksestä. Se voidaan siis nähdä virkkeenpituuden kumulatiivisena todennäköisyysjakaumana. Sen derivaatta on virkkeenpituusjakauman tiheysfunktio.
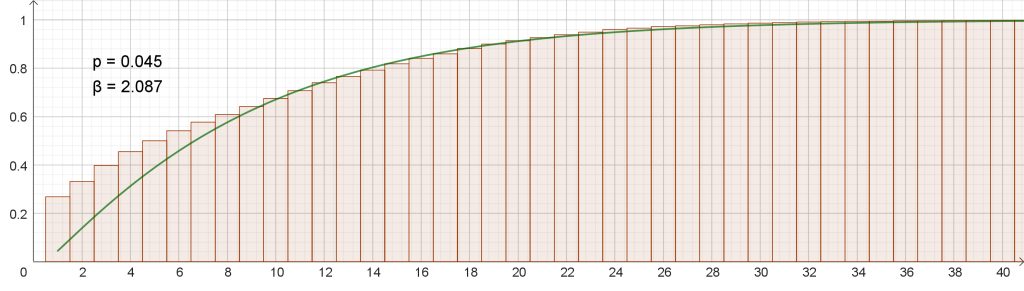
Riskifunktioita käytetään riskien ennustamiseen ja hallintaan monissa yhteyksissä, esimerkiksi terveydenhuollossa, tekniikassa ja rahoituksessa. Puolalaisten tutkijoiden käyttämän tyyppisen riskifunktion idea tulee kaukaa sadan vuoden takaa italialaisen taloustieteilijän Vilfredo Pareton kehittämästä Pareto-diagrammista [12]. Siinä esitetään todennäköisyystiheysjakauma pylväsdiagrammina ja kertymäfunktio samassa kuvassa (kuva 7).
Pareton tutkimuskohteena oli alun perin tulon- ja omaisuudenjako, mutta hänen diagrammiaan käytetään nykyään hyvin yleisesti muun muassa prosessinohjauksessa ja laadunvalvonnassa. Tätä taustaa vasten on varmaankin ymmärrettävää, että artikkelimme lähtökohtana olevan puolalaistutkimuksen [1] kirjoittajat eivät työskentele missään lingvistiikan laitoksessa, vaan Puolan tiedeakatemian ydinfysiikan instituutin kompleksisten systeemien osastossa.
Onnistumisemme puolalaistutkijoiden tiedeartikkeliin perehtymisessä osoittaa, että tavallisen matemaattisten aineiden opettajan matemaattiset valmiudet riittävät tieteellistenkin tulosten ymmärtämiseen ja jopa tutkimuksen toistamiseen pienimuotoisilla aineistoilla. Kuitenkin vasta suomenkielisten aineistojen analysointi auttoi todella ymmärtämään syvällisemmin alkuperäisen vertailututkimuksen matematiikkaa.
Tutkimuskohteen valinta puolestaan osoittaa, että matematiikkaa ei tarvita nykyään vain matemaattis-luonnontieteellisissä ja teknillisissä tehtävissä, vaan se on ajattelun ja tutkimisen väline myös kielitieteessä. Entistä enemmän olisi siis kouluopetuksessakin tuotava esille matematiikan tarvetta ja käyttömahdollisuuksia muillakin kuin perinteisillä sovellusalueilla. Matematiikka onkin nykyään kaikille kuuluvaa yleissivistystä.
Tämä tarina puhuu myös sen puolesta, että tilastomatematiikan asemaa opetussuunnitelmissa voisi olla hyvä vahvistaa. Vaativin osa tässä työssä ei nimittäin ollutkaan matematiikka ja matemaattisten työvälineiden käyttö, vaan sen ymmärtäminen, miksi puolalaiset tutkijat olivat valinneet välineekseen ja tulostensa kuvailuun juuri sellaisen kielimallin kuin olivat valinneet ja millaisista taustoista heidän ideansa kumpuavat. Niiden selvittelemisestä ainakin me kirjoittajat opimme paljon.
Kolmas matematiikan kouluopetukseen vaikuttava näkökulma, joka tuli vahvasti esille tämän artikkelin kirjoittamisen yhteydessä, ovat ohjelmointi ja matematiikan sähköiset työvälineet. Tätä tutkimusta ei olisi ylipäänsä voinut tehdä ilman apuvälineinä käytettyjä ohjelmia. Niiden hallinnasta on (toivottavasti) tulossa yhä tärkeämpi osa koulumatematiikkaa.
Eikä kyse ole vain ohjelmien teknisestä osaamisesta, vaan välineet myös muuttavat käyttäjänsä – oppijan – ajattelutapaa. Ohjelmoinnin osalta puhutaan ohjelmoinnillisesta ajattelusta (engl. computational thinking) ja muiden matematiikkatyövälineiden osalta työvälineiden kaksisuuntaisesta vaikutuksesta käyttäjän ajatteluun [13] (engl. instrumental genesis).
Neljäs ja oppimisen kannalta kaikkein tärkein seikka on se, että innostuminen ja paneutuminen ovat avain oppimiseen. Sellaista asennetta toivotamme teille opettajalukijamme ja teidän oppilaillenne.
Lähteitä ja lisää luettavaa
[1] Stanisz, Tomasz; Drożdż, Stanisław; Kwapień, Jarosław (huhtikuu 2023): Universal versus system-specific features of punctuation usage patterns in major Western languages. Saatavissa osoitteesta https://arxiv.org/pdf/2212.11182.pdf
[2] Phys.org News (20.4.2023) : Punctuation in literature of major languages is intriguingly mathematical https://phys.org/news/2023-04-punctuation-literature-major-languages-intriguingly.html
[3] Hazard functions in seven major Western languages. EurekAlert! news. American Association for the Advancement of Science osoitteessa https://www.eurekalert.org/multimedia/982665 Alkuperäinen lähde https://press.ifj.edu.pl/en/news/2023/04/19/
[4] Heikkinen, Vesa ym.: (2001): Kuvia kirjoitetusta suomesta https://www.kielikello.fi/-/kuvia-kirjoitetusta-suomesta
[5] Virtuaalinen vanha kirjasuomi osoitteessa https://vvks.it.helsinki.fi/lauseoppi/virkkeista_ja_lauseista/index.html
[6] Hakulinen, Auli ym.: Suomen tekstilauseiden piirteitä. Kvantitatiivinen tutkimus, sivu 122. Department of General Linguistics, julkaisuja 6/2015. Osoitteessa http://www.ling.helsinki.fi/~fkarlsso/hkv3.pdf
[7] Kielipankki: Korp-käyttöliittymän käyttöohjeet osoitteessa https://www.kielipankki.fi/tuki/korp/
[8] Rahikka, Mikko: Seitsemän veljestä on Poisson-jakautunut? Blogikirjoitus 13.12.2020 osoitteessa https://mikkorahikka.blog/2020/12/13/seitseman-veljesta-on-poisson-jakautunut/
[9] Project Gutenberg osoitteessa https://www.gutenberg.org
[10] Rahikka, Mikko: Tekstin virkkeiden pituus Pythonilla. Blogikirjoitus 1.6.2023 osoitteessa https://mikkorahikka.blog/2023/06/01/tekstin-virkkeiden-pituus-pythonilla/
[11] Pekkala, Juha-Matti (2020): Oppijansuomen n-grammit: korpusvetoinen tutkimus B1-kielitaitotason toistuvista monisanaisista rakenteista. Maisterintutkielma, Jyväskylän yliopisto, Kieli- ja viestintätieteiden laitos. https://jyx.jyu.fi/bitstream/handle/123456789/72179/URN\%3ANBN\%3Afi\%3Ajyu-202010156231.pdf
[12] Katso esimerkiksi Wikipedia-artikkelia Pareto-diagrammi osoitteessa https://fi.wikipedia.org/wiki/Pareto-diagrammi
[13] Silfverberg, Harry (2018): Tieto- ja viestintätekniikka matematiikan oppimisessa https://www.utupub.fi/bitstream/handle/10024/168977/Tvt\%20ja\%20mat_22_5_2018.pdf?sequence=1
Tilaa Dimension uutiskirje – saat sähköpostiisi aina kuunvaihteessa koosteen tuoreimmista artikkeleista







