Klassiset matemaattiset temput, osa 5: Miraskill
Tällä kertaa Klassinen matemaattinen taikatemppu tarjoillaan kahdella eri tavalla, pelikorteilla ja makeisilla.
Miraskill-temppu
Taikuri ottaa pelikorttipakan ja sekoittaa korttipakan niin, että noin puolet pakasta on kuvapuoli ylöspäin ja lopun kuvapuoli alaspäin. Näin sekoitettua pakkaa voidaan sekoittaa vielä lisää.
Taikuri vilkaisee vielä kerran sekaisin sekoitettua korttipakkaa ja kirjoittaa ennustuksen paperille. Teksti taitetaan piiloon, mutta paperi jää tempun ajaksi pöydälle kaikkien nähtäväksi.
Taikuri antaa pakan katsojalle. Katsoja jakaa pakasta kaksi pelikorttia pöydälle. Jos molemmat kortit ovat kuvapuoli ylöspäin, hän laittaa tämän korttiparin pöydälle eteensä oikeanpuoleiseksi pinoksi. Jos molemmat kortit olivat kuvapuoli alaspäin, hän laittaa tämän korttiparin pöydälle vasemmanpuoleiseksi pinoksi. Jos korteista toinen on kuvapuoli ylöspäin ja toinen kuvapuoli alaspäin, kortit laitetaan pöydälle ”roskakoriin” vaikka reilusti toiseen laitaan pöytää.
Taikuri pyytää katsojaa laskemaan kuvapuoli ylöspäin ja kuvapuoli alaspäin olevat pinot. Huomataan (esimerkiksi) että kuvapuoli ylöspäin olevassa pinossa on kahdeksantoista pelikorttia ja kuvapuoli alaspäin olevassa pinossa on neljätoista korttia. Taikurin kirjoittama ennustuspaperi avataan. Siinä lukee, että kuvapuoli ylöspäin olevia kortteja tulee olemaan neljä enemmän. Ennustus toteutui.
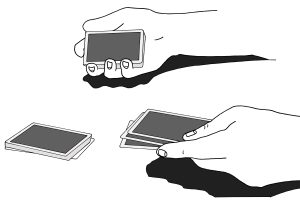
Tempun kulku tarkemmin
Tällä kertaa ei ole etukäteen tehtäviä, salaisia valmisteluita. Tarvitset korttipakan, jossa on kaikki viisikymmentäkaksi pelikorttia. Tempun alussa lasket kaksikymmentäneljä pelikorttia pöydälle yhdeksi pinoksi. Laskemisesta ei kannata tehdä numeroa, kunhan nyt jaat noin puolet korteista pöydälle. Katsojat eivät välttämättä edes tajua, että samalla lasket. Yksi tapa saada kortit laskettua, on viedä niitä pöydälle kolmen kortin nippuina. Kahdeksan tällaista niin pöydällä on kaksikymmentäneljä korttia, eikä korttien jakaminen pöydälle näytä lainkaan yksittäisten korttien laskemiselta.
Laita myös oikeassa kädessä olevat kortit pöydälle. Tässä suuremmassa pinossa on nyt kaksikymmentäkahdeksan pelikorttia. Käännä suurempi pino oikealla kädellä kuvapuoli ylöspäin.

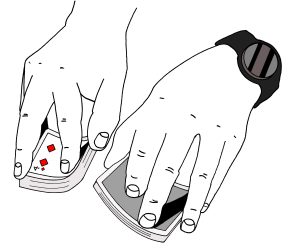
Sekoita kuvapuoli ylöspäin oleva pino kuvapuoli alaspäin olevaan, kahdenkymmenen neljän kortin pinoon kuvan osoittamalla kasinosekoituksella: viet pinot lähes kiinni toisiinsa. Nosta pinojen vastatusten olevia päitä peukaloillasi. Päästä nostettujen korttien pudota peukaloista pöydälle ja samalla työnnät pinoja hiukan yhteen. Kortit putoavat lomittain ja samalla sekoittuvat.
Sekoitus viedään loppuun työntämällä lomittain pudonneet pinot yhdeksi pakaksi. Alla oleva kolmen kuvan sarja havainnollistaa kasinosekoituksen.

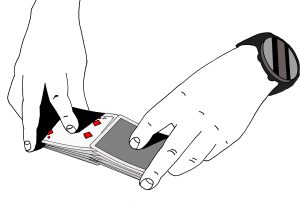
Voit toistaa sekoituksen ottamalla ensimmäisen sekoituksen jälkeen puolet pinosta ja sekoittaa sen toisen puolen kanssa uudestaan äskeisellä tavalla.
Mikäli et osaa kasinosekoitusta, voit myös yhdistää pakan työntämällä pinot päistä yhteen, ikään kuin hyppäisit yllä olevassa kuvasarjassa suoraan tuohon kolmanteen kuvaan, jossa korttipinoja työnnetään yhteen. Korttipinot menevät yhteen, vaikka kortteja ei ole plärätty lomittain. Tällainen väkisin työntö kuluttaa kuitenkin kortteja ja saattaa jopa yhdellä sekoituksella rikkoa jonkun pelikortin.
Kun olet sekoittanut pakkaa riittävän monta kertaa, anna koko pakka katsojalle. Ohjeista häntä jakamaan pakan päältä kaksi korttia ja laittamaan ne sopiviin pinoihin: kuvapuoli ylöspäin olevat kortit omaksi pinoksi, kuvapuoli alaspäin omaksi pinoksi ja kortit, joissa on sekä kuvapuoli ylös-, että alaspäin olevia kortteja omaksi roskapinoksi. Kun korttien jakamisen jälkeen kuvapuoli ylöspäin ja kuvapuoli alaspäin olevat pinot lasketaan, huomataan (tässä esimerkissä) että kuvapuoli ylöspäin olevia kortteja on neljä enemmän. Tämä täsmää tekemääsi ennustukseen.
Selityksiä
Temppu toimii lähes itsestään. Tämä on yksi niitä kiintoisia matemaattisia ilmiöitä, jotka ovat olemassa, mutta joita ei koulun matematiikan kirjoista löydy. Ilmiön voit havaita ihan tavallisella, sekoitetulla korttipakalla. Hae lähin korttipakka ja tarkista että pakassa on 52 korttia. Voit vielä sekoittaa pakan. Jaa pakasta kaksi korttia kerrallaan kuvapuoli ylöspäin. Jos molemmat ovat punaisia, herttoja tai ruutuja, laita ne omaan pinoon, johon tästä eteenpäin laitetaan kortit, kun molemmat parit ovat punaisia. Jos molemmat parit ovat mustia, patoja tai ristejä, laita ne omaan pinoon. Jos jaat pöydälle sekä mustan, että punaisen kortin, siirrä tämä pari omaan, kolmanteen pinoon. Kun jaat koko pakan, huomaat, että olet kerännyt punaisia pareja ja mustia pareja yhtä monta. Emme voi ennustaa etukäteen, montako samaa väriä olevia pareja tulee, mutta tiedämme, että yhtä monta niitä lopulta on. Tästäkin saa tuollaisenaan ennustustempun, ja vakuuttavamman tempun, kunhan poistat pakasta vaikkapa neljä mustaa korttia ja ennustat, että punaiseen pinoon kasaantuu neljä korttia enemmän kuin mustaan pinoon.
Ennustuksesta
Palataan vielä esityksen alkuun ja korttien sekoitusten jälkeen tehtävään ennustuksen. Jos otat pakasta kuvapuoli ylöspäin olevia kortteja neljä enemmän (kaksikymmentäkahdeksan kuvapuoli ylöspäin) kuin kuvapuoli alaspäin olevia kortteja (kaksikymmentä neljä kuvapuoli alaspäin), ennustat, että kuvapuoli ylöspäin olevia kortteja tulee olemaan neljä enemmän.
Ennustuksesi ei kerro korttipinoissa olevien korttien lukumäärää, ainoastaan pinojen lukumäärän erotuksen. Jos teet tätä taikuriesityksenä, etkä kerro esityksen jälkeen tempun salaisuutta, katsojien muisti ja mielikuvitus ovat puolellasi. Viimeistään seuraavana päivänä katsojat tietävät sinun ennustaneen oikein pinoissa olevien korttien lukumäärän.
Sinä määrittelet ennustuksen ja sitä kautta tempun alussa pakan kahden pinon suuruuden. Esimerkissämme pakat olivat kokoa 28 ja 24. Yhtä hyvin ne voisivat olla 30 ja 22. Tällöin ennustuksessasi lukee, että kuvapuoli ylöspäin olevassa korttipinossa on kahdeksan korttia enemmän kuin kuvapuoli alaspäin olevassa pinossa.
Uusinta
Temppu voidaan uusia erilaisella ennustuksella. Toisella kierroksella jaat erilaisen määrän kortteja ensimmäiseen pinoon kuin ensimmäisellä kerralla. Ennustuksen teet sen mukaan, paljonko kuvapuoli ylöspäin olevassa pakassa on enemmän (tai vähemmän) kortteja kuin kuvapuoli alaspäin olevassa pakassa.
Huomautuksia
Pakassa pitää olla parillinen määrä kortteja. Täydessä pakassa on viisikymmentäkaksi korttia, joten asia on valmiiksi hoidossa. Jos pakasta puuttuu kortti tai kortteja, riittää, että poistat lisää kortteja, jotta korttien määrä olisi parillinen. Voit reilusti ottaa yhden kortin pois ja sanoa, että kokonaismäärän tulee olla parillinen, koska tempussa kortteja jaetaan pareittain, kaksi kerrallaan.
Miraskill-karkkipäivä
Kirjassani Viisi Viiriäistä ja kaksi kelmiä (MFKA 2018) on sivulta 22 alkaen Miraskill-karkkipäivätemppu. Kirjan tempussa kehotan käyttämään punaisia ja sinisiä Marianne-karkkeja. Tällä hetkellä sinisiä Marianne-karkkeja ei ele tuotannossa, eikä siis myynnissäkään. Temppua pitää päivittää vaikkapa Dumle-karkeille. Temppuun tarvitset esimerkiksi punaisia ja violettisia Dumle- karkkeja. Idea on kuitenkin sama kuin pelikorteilla.

Kirjoitat lapulle ennustuksen. Taittelet lapun ja jätät sen pöydälle näkyviin. Esittelet karkkipussin ja sanot, että pussissa on sekä punaisia että violettisia karkkeja. Sekoitat vielä pussia. Pyydä katsojaa ottamaan pussista kaksi karkkia, katsomatta millaiset karkit hän pussista sieppaa. Jos molemmat karkit ovat punaisia, ne laitetaan omaan punaisten karkkien kasaan. Jos molemmat karkit ovat violettisia, ne laitetaan omaan kasaan. Jos käteen tulee sekä punainen että violettinen karkki, nämä laitetaan omaan roskakasaan, joka on riittävän kaukana kahdesta muusta karkkikasasta. Kun kaikki karkit on nostettu pussista, katsoja laskee sekä punaiset karkit, että violettiset karkit. Punaisia on esimerkiksi kaksitoista ja violettisia kahdeksan karkkia. Punaisia on neljä enemmän. Ennustuslappu avataan. Siellä lukee, että punaisia karkkeja on neljä enemmän. Ennustus pitää paikkansa.
Selityksiä
Ennen esitystä olet laittanut pussiin esimerkiksi kaksikymmentä punaista karkkia ja kuusitoista violettia karkkia. Näillä valmisteluilla ennustus pitää aina paikkansa. Punaisessa karkkipinossa tulee olemaan neljä karkkia enemmän kuin violettikarkkikasassa. Taaskaan et ennusta karkkien lukumäärää, vaan karkkien määrän erotusta.
Tempun lopussa keräät kaikki kolmen pinon karkit pussiin. Tässä yhteydessä on helppo lisätä huomaamatta pussiin esimerkiksi neljä violettia karkkia. Nyt molempia värejä on sama määrä. Ehdotat, että temppu tehdään uudestaan. Ravistat pussia, ja kirjoitat uuden ennustuksen: Molemmissa pinoissa on yhtä monta karkkia. Kun katsoja on jakanut taas karkit punaisiin ja violettisiin kasoihin ja roskakasaan, huomataan että punaisia ja violettisia karkkeja on yhtä monta. Tekemäsi ennustus täsmää taas.
Historiaa
Steward James (1908–1996) löysi tämän kiintoisan matemaattisen ilmiön ja julkaisi sen Miraskill – nimisenä myyntitaikatemppuna vuonna 1935. James yritti markkinoida tempun käsikirjoitusta. The Linking Ring lehdessä olleesta mainoksesta huolimatta James sai myydyksi vain yhden käsikirjoituksen. James näytti ideaansa taikuriystävilleen ja lopulta joku oli esittänyt tämän tempun Ted Annemannille. Hän julkaisi käsikirjoituksen The Jinx -lehdessään syyskuussa vuonna 1936. Nyt Miraskill sai arvoisansa huomion. Temppua on sen jälkeen julkaistu lukuisia kertoja eri versioina. Se löytyy myös Jean Hugardin kirjasta Encyclopedia of Card Tricks (1937, useita painoksia) sekä Stewart Jamesin kirjasta In Print: The First 50 Years (1989). Tuossa kirjassa James kertoo myös tempun historiasta. Allan Slaightin kirjaan The James File, Volume Two on kerätty eri julkaisuista parikymmentä temppua, joiden metodi perustuu Miraskill periaatteeseen.
Jamesin alkuperäinen temppu tehdään pelikorteilla, mutta eri tavalla kuin tämän artikkelin versio. Tämän jutun versio on lähempänä Karl Fulvesin kirjassa More Self-Working Card Tricks (Dover 1987) sivulla 7 nimellä Miraskil (vain yksi L-kirjain) sekä Bob Longen kirjassa The Magical Math Book (Sterling Publishing Co., Inc, 1997) sivulla 38 nimellä Simple Miraskill julkaistuja versioita. Sekä Fulves että Longe ovat molemmat keksineet saman idean toisistaan tietämättä, mutta Fulves on julkaissut versionsa aiemmin. Karl Fulves esitteli ideaa käyttää kuvapuoli ylöspäin tai alaspäin olevia pelikortteja jo vuonna 1968 kirjassaan Principles of Riffle Shuffle Set-Ups tempussa nimeltään Future Perfect. Fulvesin kirja on omakustanne, joten se on hyvinkin voinut jäädä Bob Longelta näkemättä.
Miraskill kuvapuoli ylöspäin tai alaspäin olevia pelikorteilla on siitä käytännöllinen, että korttien määrän vaihtelun voi tehdä katsojien silmien edessä vain jakamalla kortit kahteen pinoon niin, että toiseen, kuvapuoli ylöspäin tulevaan pinoon, tulee haluamasi määrä kortteja enemmän. Yhtään korttia ei tarvitse ottaa salaa pakasta pois.
Karamelli-idea kahden värisillä Marianne-karkeilla on kulkenut matkassani matemaattisten taikatemppujen työpajoissani 2010-luvun alusta lähtien. Karkit tuovat monella tavalla vaihtelua matemaattisiin taikatemppuihin, jotka muutoin ovat pelikorttipainotteisia. Lisäksi todistusaineistosta pääsee miellyttävällä tavalla eroon, jos tempun selitystä ei ole tarkoitus paljastaa. Karkkien käyttö on sekin alun perin Steward Jamesin idea, vaikka tämä asia selvisi minulle vasta viime vuonna. Vanhojakin lehtiä pitäisi lukea tarkasti. Samaisessa The Jinx lehden syyskuun numerossa vuonna 1936 on Jamesin temppu The Candy King. Tempun metodi perustuu Miraskill-ideaan ja siinä käytetään makeisia.
Kirjoittaja
Martti Sirén on hämeenlinnalainen taikuri, tietokirjailija, työpajakouluttaja, taikuuden historian penkoja, tarinoiden kertoja, joskus myös koulujen opetussuunnitelmien ulkopuolelta löytyvien ja karkeillakin esitettävien matemaattisten ilmiöiden kertoja. Sirén on kirjoittanut neljä kirjaa matemaattisista taikatempuista ja pitänyt matemaattisten taikatemppujen työpajoja opettajille yli viidentoista vuoden ajan.
Edellinen taikuriartikkeli: Klassiset matemaattiset taikatemput, osa 3: Salama-arviointi (5.12.2023)
Tilaa Dimension uutiskirje – saat sähköpostiisi aina kuunvaihteessa koosteen tuoreimmista artikkeleista







