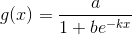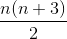Mikko Rahikan GeoGebra-sarja – Osa 2: Sovituskomennot GeoGebrassa
Funktion sovittaminen pisteistöön on tyypillinen ongelma, jonka ratkaisemiseminen onnistuu mukavahkosti tietokoneohjelmien avulla. GeoGebrassa on oma työkalu sovitusongelmien ratkaisuun. Lisäksi ohjelmassa on runsaasti sovituskomentoja.
Tutkitaan ensin Kahden muuttujan regressio -työkalua. Seuraavissa esimerkeissä käytetään kuvan taulukkolaskennan lukuja. Kirjoitan GeoGebran komennot ja käyttöliittymään liittyvät sanat lihavoituina ja komentojen englanninkieliset käännökset kursiivilla.
Kuva 1.
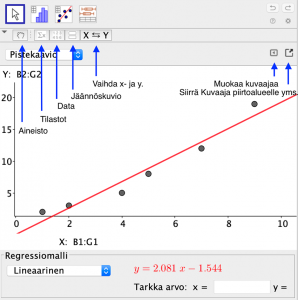
Valitaan taulukkolaskennan alue B1:G2 ja työkalu Kahden muuttujan regressioanalyysi (Kuva 1). Avautuvassa ikkunassa valitaan Analysoi ja GeoGebra avaa Data-analyysi-ikkunan. Regressiomalli-valikosta voi valita erilaisia sovituksia: Lineaarinen, Logaritminen, Polynomi, Potenssi, Eksponentiaalinen, Kasvu, Sin ja Logistinen (Kuva 2).
Kuva 2.
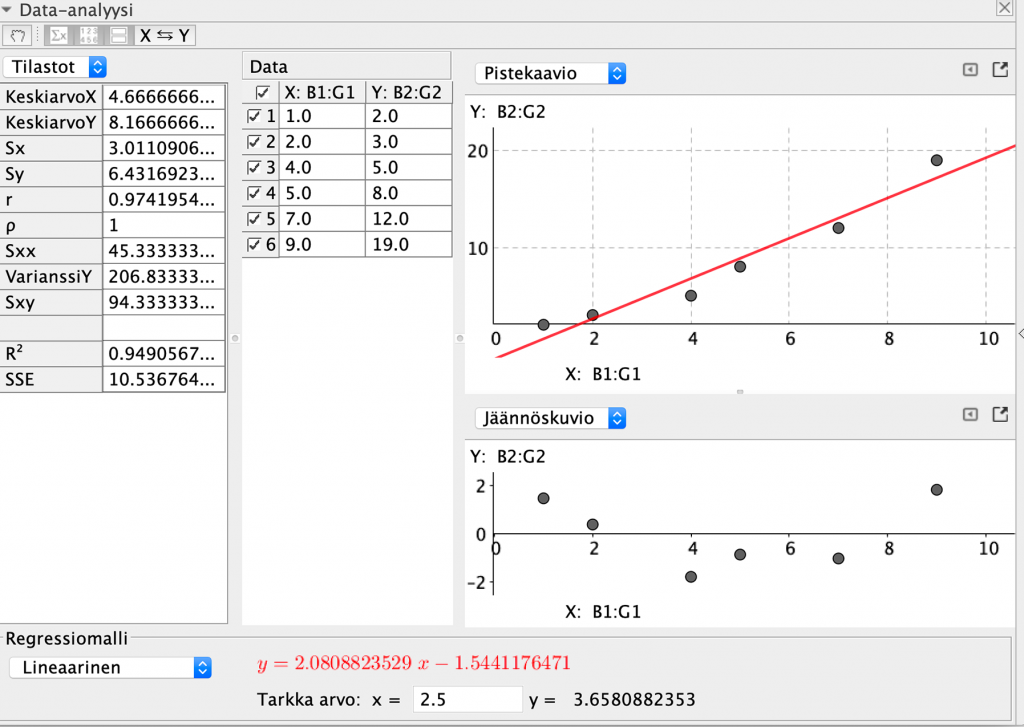
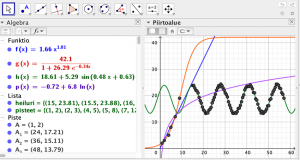
Ikkunan vasemman yläreunan käsi -ikonin avulla voi muuttaa valittua lukualuetta taulukkolaskennassa, seuraava ∑x -painike näyttää tilastollisia tunnuslukuja liittyen sovitukseen, seuraava painike näyttää mittausdatan, seuraava jäännöskuvion ja viimeinen vaihtaa datan x– ja y-koordinaatit keskenään. Data-ikkunassa voi poistaa yksittäisiä pisteitä ja Jäännöskuvio kertoo pisteiden y-koordinaattien poikkeaman pystysuunnassa valitusta sovituskäyrästä. Oikean yläkulman pienen kolmion takaa löytyy ikkuna, jossa voi lisätä viivadiagrammin, ruudukon ja muuttaa kuvaajan mittasuhteita. Kolmion oikealla puolella olevan pikkuneliön avulla saa kuvaa kopioitua suoraan piirtoalueelle. Siellä on helpompi muokata akseleita ja lisätä akseleille nimet ja yksiköt. Samalla kun kuvaaja siirtyy piirtoalueelle, niin myös Algebra-ikkunaan ilmestyy sovitettu funktio (Kuva 3).
Kuva 3.
Tarkastellaan sitten syöttökentässä ja CASissa käytettäviä sovituskomentoja. Kahden muuttujan regressio -työkalun regressiomallifunktiot käyttäytyvät samalla tavoin kuin sovituskomennot. Komennot tarvitsevat syötteekseen pistelistan. Ennen kuin pistelista luodaan, niin kannattaa käydä valitsemassa Asetukset→Nimeäminen→Nimeäminen pois. Näin pisteiden nimet eivät ilmesty piirtoalueelle. Valitaan taulukkolaskennan alue B1:G2 ja työkalu Luo pistelista (Kuva 4).
Kuva 4.
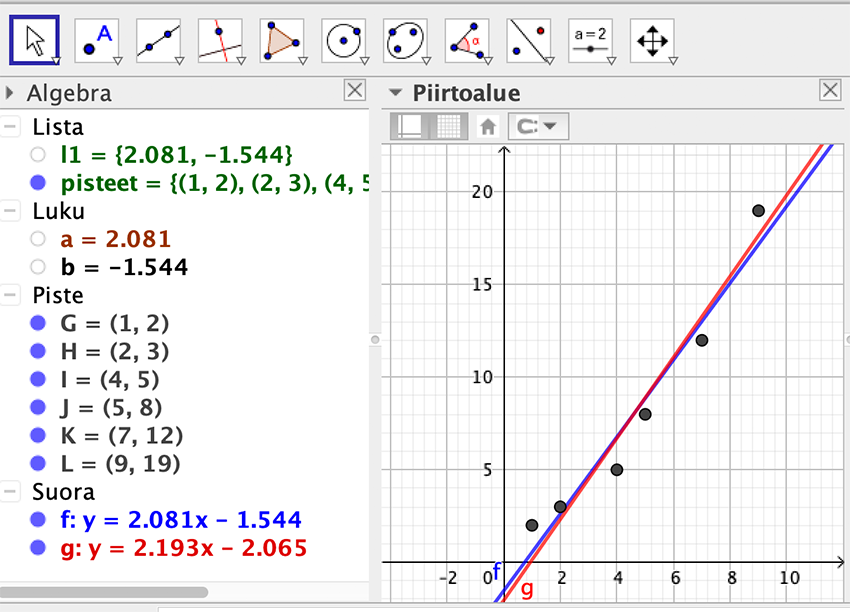
Avautuvassa ikkunassa voi muuttaa pistelistan nimen, oletuksena se on l1. Annetaan pistelistalle nimi ”pisteet”. Komento SovitaSuora(pisteet) (FitLine) sovittaa pienimmän neliösumman avulla suoran pisteisiin ja antaa sille nimen f. Komento SovitaSuoraX(pisteet) (FitLineX) tekee saman sovituksen, mutta vaihtaa x– ja y-koordinaatit sovitusalgoritmissa. Normaalitilanteessa pienimmän neliösumman sovituksessa ajatellaan, että x-koordinaatit ovat riippumattomia (selittäviä) ja y-koordinaatit riippuvia (selitettäviä) muuttujia. SovitaSuoraX muuttaa y-koordinaatit riippumattomiksi sovitusalgoritmiin (Kuva 5).
Kuva 5.
Sovitetun suoran kulmakertoimen arvon (kuvassa muuttuja a) saa komennolla Kulmakerroin(f) ja vakiotermin arvon (kuvassa muuttuja b) hieman hankalammin Alkio(Kertoimet(f(x),2)). Kertoimet luo listan polynomin f(x) kertoimista ja Alkio(lista, 2) poimii listan toisen jäsenen eli tässä tapauksessa vakiotermin. SovitaSuora-komento poikkeaa muista sovita-komennoista, sillä se tuottaa suoran yhtälön, muut sovita-komennot tuottavat funktion.
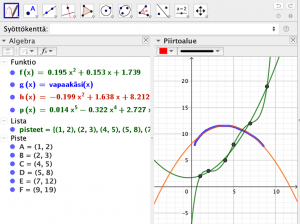
Polynomisovitukset tuotetaan komennolla SovitaPolynomi(<Pistelista>, <Polynomin asteluku>) (FitPoly). Komento SovitaPolynomi(pisteet, 2) luo toisen asteen funktion. Pistelistan tilalla voi olla myös vapaalla kädellä piirretty funktio. Sellaisen saa luotua Piirtoalueen Vapaakäsi-työkalulla. Kuvassa f(x) on toisen asteen sovitus ja p(x) viidennen asteen sovitus pisteet listaan. Funktio h(x) on paraabelisovitus vapaalla kädellä piirrettyyn funktioon g(x). Algebraikkunassa olevia funktioita voi derivoida, integroida Syöttökentässä tai CAS:issa ja myös niiden ominaisuuksia voi tutkia Funktion-analysointi -työkalulla. Se löytyy Piirtoalueen työkaluista Kulma-työkalun ”takaa” (Kuva 6).
Kuva 6.
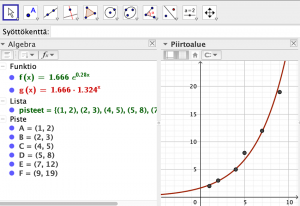
Eksponentiaalista kasvua varten on sovitukset SovitaEksp (FitExp) ja SovitaKasvu (FitGrowth). SovitaEksp(pisteet) tuottaa muotoa $ f\left(x\right)=a\cdot e^{b\cdot x} $ olevan funktion ja SovitaKasvu tyyliin $ g\left(x\right)=a\cdot b^x$. GeoGebran kannalta kyseessä on sama funktio, vain esitystapa on erilainen. Mikäli tarvitset laskuissasi luonnollisen logaritmin kantalukua $ e $, niin sen saa GeoGebrassa näppäinkomennolla Alt-e tai Syöttökentän oikean reunan symbolivalikosta. GeoGebra 6:ssa $ e $ ja $ π $ löytyvät myös virtuaalinäppäimistöltä. Näiden komentojen syötelistan y-koordinaattien tulee olla samanmerkkisiä (Kuva 7).
Kuva 7.
SovitaPotenssi(pisteet) (FitPow) sovittaa funktion, joka on muotoa $ f\left(x\right)=a\cdot x^b $. Pistelistan x– ja y-koordinaattien tulee olla positiivisia.
SovitaLogist(pisteet) (FitLogistic) sovittaa muotoa
olevan logistisen funktion. Pistelistan y-koordinaattien tulee olla positiivisia. Pisteiden pitää olla myös riittävästi S:n muotoisella käyrällä.
SovitaLog(pisteet) (FitLog) sovittaa muotoa $ p\left(x\right)=a+b\ln\left(x\right) $ olevan funktion. Pisteiden x-koordinaattien tulee olla positiivisia.
Sin-sovitusta varten toin taulukkolaskentaan heiluriin liittyvää mittausdataa. Loin datasta pistelistan nimeltä ”heiluri”. SovitaSini(heiluri) (FitSin) tuottaa muotoa $ h\left(x\right)=a+b\sin\left(cx+d\right) $ olevan funktion. Kokemus osoittaa, että jos pisteitä on runsaasti, suuruusluokkaa satoja, niin komento ei toimi aina täydellisesti (Kuva 8).
Kuva 8.
Usein kun sovitetaan mittausdataa, tulee tarve määrittää itse sovitusfunktio. Jos haluaa pakottaa sovitussuoran tai paraabelin kulkemaan origon kautta, niin komennolla Sovita(<Pistelista>, <Funktiolista>) (Fit) se onnistuu. GeoGebra määrittää funktiolistan kertoimet sovituskäyrälle. Niinpä Sovita(pisteet, {x}) sovittaa origon kautta kulkevan suoran ja Sovita(pisteet, {x, x^2}) origon kautta kulkevan toisen asteen polynomin.
Ehkä mielekkäämpi tapa käyttää Sovita-komentoa on kirjoittaa sovitettava lauseke komennon syötteeksi tyyliin Sovita(<Pistelista>, <Funktio>). Origon kautta kulkeva suora olisi sovitettu komennolla Sovita(pisteet, k x).
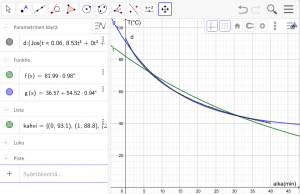
Syksyn 18 fysiikan ylioppilaskokeessa oli tehtävä, jossa oli mittaustuloksia kahvin lämpötilasta ajan funktiona. Luodaan mittaustuloksista pistelista kahvi. Mittaustulokset näyttävät noudattavan Newtonin jäähtymislakia. Komento Sovita(kahvi, a b^x + c) tuottaa funktion, joka kulkee melkoisen hyvin pisteiden kautta. Tosin pisteiden alku- ja loppupäät poikkeavat selvästäsi mallin tuottamasta käyrästä. Komentoa käytettäessä GeoGebra luo vakioita vastaavat liu’ut. Lisäksi pitää tarkistaa Algebra-ikkunasta, että vakioina käytettävät muuttujat eivät ole aiemmin määriteltyjä.
Splini(<Pistelista>) -komento (Spline) luo pistelistan pisteiden kautta kulkevan splinikäyrän. Splini on paloitellusti määritelty parametrinen käyrä. Palat koostuvat kolmannen asteen käyristä siten, että liitoskohdissa käyrä on jatkuva ja derivoituva. Toki käyrän derivoiminen ei onnistu kovin helposti, koska kyseessä on parametrinen käyrä. Käyrälle voi piirtää tangentin jokaiseen pisteeseen. Korkeamman asteen splinejä saa syntaksilla Splini(<Pistelista>, <Asteluku ≥ 3>). Splinejä ei kannata käyttää, jos mittaustuloksissa on paljon ”virhettä”, koska käyrä kulkee kaikkien pisteiden kautta ilman pehmennystä (Kuva 9).
Kuva 9.
Kuvassa f(x)=SovitaKasvu(kahvi), g(x)=Sovita(kahvi, a+b*c^(x)) ja d: Splini(kahvi).
Mittaustuloksien käsittelyn apuna toimii myös Datafunktio(<Lukulista>, <Lukulista>) (Datafunction). Sen toimintaa on käsitelty edellisessä artikkelissani ”Listat GeoGebrassa”, Dimensio 6/2018.
Implisiittinen sovittaminen pyrkii tuottamaan n:n asteen xy-tasokäyriä. Pisteiden lukumäärän tulee olla vähintään
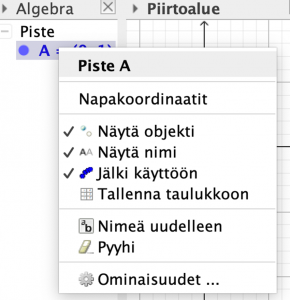
Yritetään piirtää vapaalla kädellä tietokoneen hiirellä yksikköympyrä mahdollisimman hyvin. Luodaan ensin piste A = (0,1). Jotta pisteen koordinaatit saadaan tallentumaan taulukkolaskentaan, sen ikkunan tulee olla näkyvissä, eli Näytä-valikossa Taulukkolaskennan kohdalla tulee olla ✓-merkki (Kuva 10).
Kuva 10.
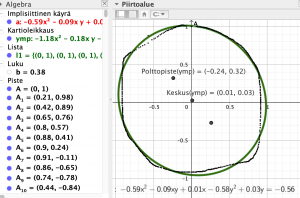
Valitaan hiiren oikealla painikkeella piste A ja avautuvasta valikosta Tallenna taulukkoon. Kun avautuneen ikkunan sulkee, voi alkaa liikuttaa pistettä A ja pisteen koordinaatit tallentuvat taulukkolaskentaan. Kun taulukkolaskennassa valitaan A:n liikkuessa luodut pisteet ja Luo pistelista, niin pisteet ilmaantuvat piirtoalueelle ja oletuksena syntyy lista l1. Komennolla SovitaImplisiittisesti(l1, 2) (FitImplicit) ohjelma tuottaa toisen asteen käyrän. Algebraikkunassa GeoGebra ilmoittaa, että se on ”Implisiittinen käyrä”. Katsomalla sitä tunnistan tai paremminkin arvaan, että kyseessä on ellipsi. Kokeile itse korkeamman potenssin sovituksia ja jos olet rohkea, niin pohdi miten algoritmit ovat niihin päätyneet.
Jostain kumman syystä GeoGebra ei tunnista, että implisiittinen käyrä a on oikeasti kartioleikkaus. Niinpä syöttökentän komennolla ymp = a ohjelma luo kartioleikkauksen siten, että se toimii GeoGebran kartioleikkauskomentojen kanssa. Kartioleikkausten symmetriakeskus saadaan komennolla Keskus(ymp), polttopisteet Polttopiste(ymp) ja ellipsin eksentrisyys komennolla Eksentrisyys(ymp) (Kuva 11).
Kuva 11.
Mikäli haluat tutusta monipuolisiin esimerkkeihin GeoGebra sovituskomennoista, niin kannattaa hankkia ruotsalaisten ystävieni Jonaksen ja Thomaksen ”Mathematical Modeling, Applications with GeoGebra” -kirja. Kirjassa on useita kymmeniä pisteistön sovittamiseen liittyviä esimerkkejä liittyen muun muassa kemiaan, fysiikkaan, lääketieteeseen ja taloustieteeseen. Tätäkin kirjoittaessa olen selannut kirjaa aika paljon.
Lue lisää:
Korhonen, Luoma-aho, Rahikka. Geogebra -opas. MFKA 2012.
Hall, Lingejärd. Mathematical Modeling: Applications with GeoGebra. Wiley 2017. Kirjan materiaalisivu: http://bcs.wiley.com/he-bcs/Books?action=index&itemId=1119102723&bcsId=10240
GeoGebran käyttöohjeen Fit-komennon wiki-sivu https://wiki.geogebra.org/en/Fit_Command
Mikon fysiikan blogi https://mikonfysiikka.wordpress.com/
Rahikka, M. Listat GeoGebrassa. Dimensio 6/2018.
Spline Wikipediassa. https://en.wikipedia.org/wiki/Spline_(mathematics)