Kuvien piirtäminen matematiikan tehtäviin Geogebralla
Tuomo Riekkinen esitteli Dimensiossa (1.2.2022) Inkscapea matematiikan tehtävien kuvittamiseen. Miksi käyttää piirustusohjelmaa, kun matematiikan työvälinekin on olemassa? Hyöty ei silloin jäisi vain kuvan tuottamiseen, vaan samalla tulisi harjaantumista, josta olisi hyötyä monessa muussakin matematiikan tehtävässä ja aihepiirissä. Olennainen kysymys onkin, tukeeko ja kehittääkö piirustusohjelma kuvantekijän matemaattista ajattelua yhtä hyvin kuin dynaaminen matematiikkaohjelma.
Käytän esimerkkinä Geogebraa. Siinä on paljon valmiita kuviotyövälineitä kuten muunneltava monikulmio, jäykkä monikulmio, säännöllinen monikulmio, ympyrä jne., mutta suorakulmiota ei ole. Piirto-ohjelmassa on sen sijaan suorakulmiotyöväline ja siksi liikkeellelähtö on näennäisesti helpompaa. Kuitenkin, kun suorakulmion on kerran konstruoinut Geogebrassa, niin tiedoston voi tallentaa ja ladata sitten uuden kuvan pohjaksi.
Suorakulmion muotoa, kokoa ja asentoa voi muuttaa nurkkapisteitä siirtämällä. Nurkkapisteet voi piilottaa kaikki tai yksitellen. Geogebra nimeää kuvion ja sen osat automaattisesti, mutta nimiä ei tarvitse näyttää, jos ne eivät ole tarpeen. Ohjauspisteet kannattaa pitää näkyvissä niin kauan kunnes kuva on lopullisessa muodossaan. Suorakulmio on geometrinen objekti, joten Geogebra pystyy näyttämään sen pinta-alan tai sivujen pituudet, jos niin halutaan (kuva 1). Jos kyse on vain mallikuvasta, niin suorakulmio on helpointa piirtää monikulmiotyökalulla käyttäen hyväksi koordinaatioruudustoa.
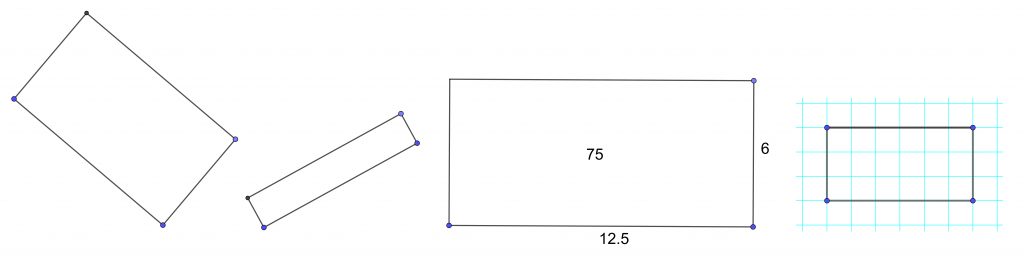
Suunnikas on myös piirrettävä ensimmäisellä kerralla alusta alkaen ominaisuuksiensa perusteella. Tässä on kaksi erilaista mahdollisuutta. Se voidaan piirtää joko kolmesta nurkkapisteestä tai nurkkapisteistä ja kärkikulmasta muunnettavaksi (kuva 2). Kuvion reunaviivan ja sisäosan väritys ovat vapaasti valittavissa, myös yksittäisen sivun väri ja viivan paksuus. Matematiikkaohjelman tehokkuus kuvien piirtämisessä alkaa näkyä sitä selvemmin, mitä useampia yksityiskohtia kuvaan halutaan.

Neliön niin kuin muidenkin säännöllisten monikulmioiden piirtämiseen Geogebrassa on valmis toiminto. Silloin minkä tahansa säännöllisen monikulmion piirtäminen on yhtä helppoa kuin neliön. Toiminnolle annetaan parametreina kaksi pistettä ja kärkien lukumäärä. Niitä ei siis tarvitse edes luoda erikseen etukäteen (kuva 3).
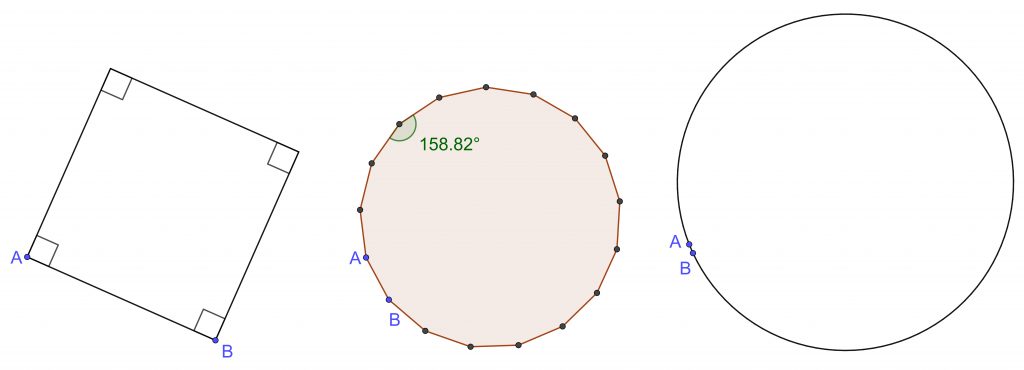
Ympyrän käsittelyssä on paljon samaa niin Geogebrassa kuin piirto-ohjelmassakin, vaikka piirtämisen lähtökohdat ovat erilaiset. Geogebrassa on kolme eri ympyrätoimintoa. Niiden parametrit ovat keskipiste ja kehän piste tai keskipiste ja säteen pituus tai kolme kehän pistettä. Kahdessa ensin mainitussa tapauksessa lähdetään keskipisteestä niin kuin harpilla piirrettäessä. Kolmannessa tapauksessa annetaan kolme mielivaltaista pistettä. Ympyrän keskipiste on tällöin määritettävä erikseen (kuva 4). Käytettävissä on myös valmis keskipistetoiminto. Silloin ei tarvita mitään geometrista ajattelua, sillä riittää vain valita keskipistetyöväline ja antaa parametriksi ympyrä osoittamalla sen kehää!
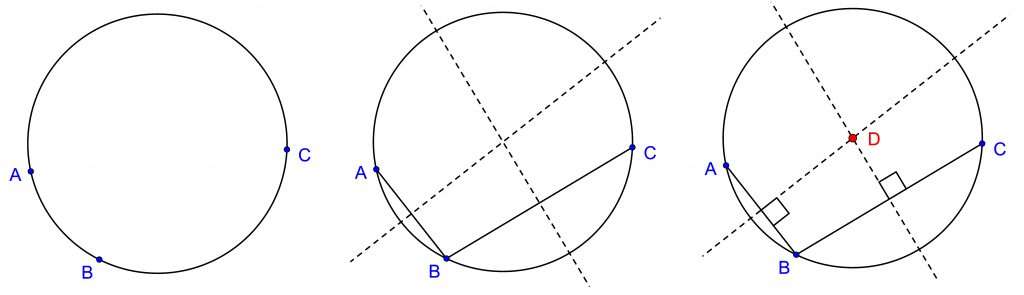
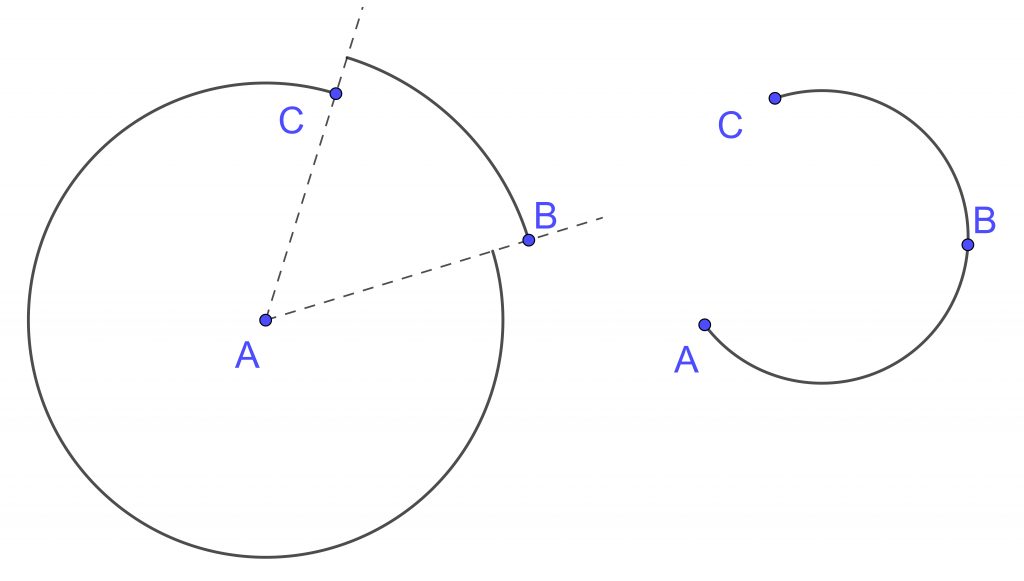
Myös ympyränkaaren piirtämiseen Geogebrassa on kaksi toimintoa: kun tunnetaan keskipiste ja kaksi pistettä tai kolme kaarella olevaa pistettä. Ensimmäisessä tapauksessa ensimmäinen parametri on keskipiste, toinen parametri määrää kaaren oikean päätepisteen (suunta keskuskulman mielessä) ja siis säteen, sekä kolmas kaarta vastaavan keskuskulman vasemman kyljen suunnan. Siten pisteparien BC ja CB määrittämät keskuskulmat ovat eksplementtikulmia, mutta säteet voivat eri pituiset, vaikka keskipiste olisi sama A (kuva 5, vasen). Jos pisteet A, B ja C ovatkin halutulla kaarella, niin saadaan kolme erilaista kaarta.
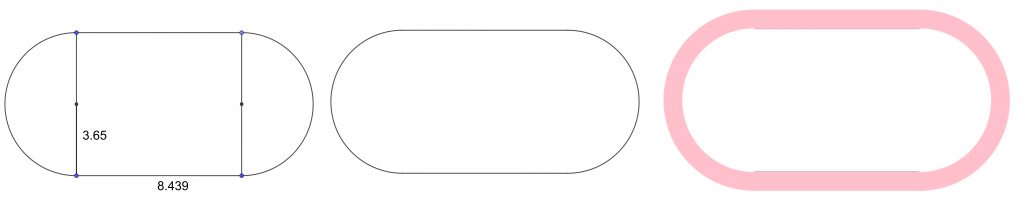
Yhdistelmäkuviot ovat aina erikoistapauksia. Niinpä niiden piirtämiseen on monta eri tapaa. Tarkastelen esimerkkinä Tuomon käyttämän soikion asemesta urheilukentän juoksuradan muotoista kuviota. Takasuoran pituus on 84,39 ja päätykaarteen ympyrän säde 36,50 metriä. Geogebran piirtoalueelle sopiva mittakaava on 1 : 1000, jolloin siis 1 cm vastaa 10 metriä. Peruskuvion piirtäminen (kuva 6, vasen) käy helposti, kun piirretään keskussuorakulmio oikean muotoiseksi käyttäen lähtökohtana kuvaa 1 varten piirrettyä suorakulmiota ja sitten päätyihin puoliympyrät. Nurkkapisteet saadaan raahatuiksi täsmälleen oikeille kohdille suurentamalla kuviota riittävästi piirtämisen ajaksi.
Juoksuradan sisäreunan (kuva 6, keskellä) soikio saadaan tästä piilottamalla tarpeettomat osat. Juoksuratojen alueen piirtämiseen (kuva 6, oikealla) on varmaan monta mahdollisuutta. Itse tein sen niin, että piirsin keskussuorakulmion lyhyempien sivujen keskipisteet keskipisteenä oikeankokoiset puoliympyrät, jotka väritin. Sitten nostin kentän keskiosan päätypuoliympyrät yhtä tasoa ylemmäs, joten ne peittivät juoksuratojen sisäpuolelle jäävät alueet isoista puoliympyröistä. Kuvioiden sijoittaminen eri kerroksiin on kätevä ominaisuus Geogebrassa. Se on selvästi lainattu piirto-ohjelmista, joissa se on yleensä vakiovarusteena. Lopuksi piirsin etu- ja takasuorat suorakulmioina (kuva 6, oikea). Juoksurata-alueen piirtämisessä on monta vaihetta eikä sen piirtäminen Geogebralla ole niin ollen ehkä sen helpompaa kuin piirto-ohjelmallakaan.
Silloin kun tehdään kuvitusta johonkin julkaisuun, olipa se sitten kirja tai Tuomon mainitsema MAOLin koekysymysprojekti, on tietysti tehokkainta käyttää sitä työvälinettä, jonka käytön kuvittaja osaa parhaiten. Sen sijaan omaa oppimateriaaliaan tai kokeitaan tekevän opettajan kannattaa harkita vakavasti matematiikkaohjelman, esimerkiksi Geogebran, käyttämistä. Se tuottaa mittatarkat kuvat monesti helpommin kuin piirustusohjelma. Samalla opettaja kehittää matemaattista ajatteluaan ja oppii niksejä, joista on apua oppilaiden opastamisessa. Oppilaiden kohdalla valinta on vielä tärkeämpi. Edellä olen yrittänyt esittää ratkaisuja, joista näkyisi, että Geogebra on ainakin yhtä helppo matemaattisten kuvien tuottamisessa kuin piirustusohjelma. Lisäksi Geogebra on aivan ylivoimainen funktio-opissa. Aikaa ei kannata tuhlata monien ohjelmien opetteluun, sillä on parempi osata yksi ohjelma hyvin kuin monta huonosti.
Tilaa Dimension uutiskirje – saat sähköpostiisi aina kuunvaihteessa koosteen tuoreimmista artikkeleista