Kvanttimekaniikan peruskysymyksiä: yhdistetyt systeemit ja kvanttikietoutuminen

Tiede ja teknologia

17.6.2021

Kvanttimekaniikan aito todennäköisyysluonne, puhtaiden tilojen superpositiot, tiettyjen suureparien yhteensopimattomuus, mittausten aiheuttamat väistämättömät häiriöt sekä preparointeihin ja mittauksiin liittyvät epätarkkuusrelaatiot ovat kvanttimekaniikan keskeisiä klassisesta fysiikasta poikkeavia piirteitä. Niitä esiteltiin ns. kaksitasosysteemien eli kubittien teorian puitteissa Dimension artikkelissa Kvanttimekaniikan peruskysymyksiä: yhteismittauksista ja epätarkkuuksista. [1] Kun yksittäisen fysikaalisen systeemin, esimerkiksi juuri kubitin, sijasta tarkastellaan useampia systeemejä, niin kvanttimekaniikan todennäköisyysluonteesta paljastuu uusia klassisesta fysiikasta poikkeavia piirteitä.

Klassisessa mekaniikassa kaksi identtistä, läpäisemätöntä systeemiä, esimerkiksi massapistettä, voidaan erottaa toisistaan nimeämällä ne: tämä on se systeemi, joka hetkellä $t_0$ oli avaruuden pisteessä $\mathbf r(t_0)$ ja jolla oli nopeus $\mathbf v(t_0)$. Nimi säilyy kausaalisessa evoluutiossa. Teorian aidon todennäköisyysluonteen johdosta tällainen nimeäminen ei kvanttimekaniikassa ole mahdollista. Esimerkiksi heliumatomin kahta elektronia ei voida näin pysyvästi erottaa toisistaan. Tällä seikalla on keskeinen merkitys esimerkiksi juuri atomien ja molekyylien kvanttifysiikassa. Identtisten systeemien erottumattomuudesta seuraa perustavanlaatuisia rajoituksia identtisistä systeemeistä koostuvan yhdisteen tila- ja suurejoukoille.

Toinen merkittävä uusi piirre, joka saadaan dramaattisimmin esille juuri yhdistettyjen systeemien kvanttiteoriassa, on kvanttikietoutuminen tai kvanttilomittuminen, osasysteemien mahdollinen vahva (vuorovaikutukseton) probabilistinen toisiinsakytkeytyminen. Puhtaiden tilojen superposition lisäksi juuri kvanttikietoutuminen on keskeinen elementti kehittyvässä kvanttiteknologiassa.

Tässä kirjoituksessa esitellään yhdistettyjen systeemien kvanttimekaniikan erityispiirteitä rajoittuen taas matemaattisesti yksinkertaisimpaan malliin, jossa yhdiste koostuu äärellisestä määrästä kaksitasosysteemejä. Päähuomio on kvanttikietoutumisessa joskin esittelemme kirjoituksen lopussa lyhyesti myös identtisten systeemien peruskysymyksen.

Kirjoitus on jaettu kuuteen lukuun. Luvussa 1 palautetaan mieliin kvanttimekaniikan perusrakenne ja esitellään yhdistettyjen systeemien teorian perusta, jota sovelletaan luvussa 2 kubittipareihin. Luku 3 esittelee kvanttimekaniikan yhden oudoimmista piirteistä, kvanttikietoutumisen. Luvussa 4 tarkastellaan kvanttikietoutumista ja klassisia teorioita luonnehtivia Bellin epäyhtälöitä. Luvussa 5 esitellään kietoutumisen esimerkkeinä vuorovaikutuksettoman tiedonsiirron mahdollistama kvanttiteleportaatio sekä yksi peliteoreettinen sovellus. Luvussa 6 esitellään lyhyesti objektien erottumattomuudesta aiheutuvia rajoituksia.

1. Teoreettinen lähtökohta

Artikkelissa [1] seurattiin ns. tilastolliselle kausaliteetille perustuvaa yleistä tilan ja suureen käsitteille rakentuvaa teorianmuodostusta, jossa systeemin jokainen tila $s\in\boldsymbol{S}$ ja suure $O\in\boldsymbol{O}$, arvojoukolla $(\Omega,\mathcal{A})$, määrittelee todennäköisyysmitan $p^O_s:\mathcal{A}\to[0,1]$, jonka merkitys on seuraava: luku $p^O_s(X)$ on todennäköisyys jolla suureen $O$ mittaus tilassa $s$ tuottaa tuloksen joukosta $X$. Asettamalla tilajoukolle $\boldsymbol{S}$ sekä suurejoukolle $\boldsymbol{O}$ sopivia ehtoja, näin muotoillun teorian rakenne voidaan täsmentää kvanttimekaniikan Hilbertin avaruus -teoriaksi, siis ääretönulotteisen kompleksisen separoituvan Hilbertin avaruuden operaattoriteorialle rakentuvaksi teoriaksi. Minimoiden tarvittavan matematiikan osuutta artikkelissa tarkasteltiin pääasiassa juuri kubittimallia.

Kertaus 1. Kubittimallissa systeemin Hilbertin avaruus voidaan valita kaksiulotteiseksi kompleksiseksi vektoriavaruudeksi $\mathbb C^2$, jolloin kubitin tilat saadaan positiivisina jäljen yksi operaattoreina, $2\times 2$-matriiseina $\rho_{\boldsymbol{n}}=\frac 12(I+\boldsymbol{n}\cdot\mathbf\sigma)$, $\boldsymbol{n}\in\mathbb R^3, \left\|\boldsymbol{n}\right\|\leq 1$, (kaksiarvoiset) suureet efektiarvoisina kuvauksina $\mathsf{E}(\{\pm 1\})=E_\pm$, missä $E_+$=$\frac 12(e_0I+\boldsymbol{e}\cdot\mathbf\sigma)$, $E_-$=$I-E_+$, ja $\left\|\boldsymbol{e}\right\|\leq\min\{e_0,2-e_0\}$, ja todennäköisyyksiksi luvut $p^{\mathsf{E}}_{\rho_{\boldsymbol{n}}}(\{+1\})$=${\mathrm{tr}\left[{\rho_{\boldsymbol{n}}E_+}\right]}$=$\frac 12(e_0+\boldsymbol{n}\cdot\boldsymbol{e})$, ja $p^{\mathsf{E}}_{\rho_{\boldsymbol{n}}}(\{-1\})$=$1- p^{\mathsf{E}}_{\rho_{\boldsymbol{n}}}(\{+1\})$. Luonnollisesti suureen $\mathsf{E}$ mahdollisiksi mittaustuloksiksi voidaan valita mikä tahansa luku- tai symbolipari.

Puhtaat tilat ja tarkat suureet erottuvat idempotenttisuusehdoilla $\rho_{\boldsymbol{n}}^2=\rho_{\boldsymbol{n}}$ ja $E_\pm^2=E_\pm$, jotka tässä mallissa voidaan yhtäpitävästi antaa geometrisina ehtoina $\left\|\boldsymbol{n}\right\|=1$ ja $e_0=1=\left\|\boldsymbol{e}\right\|$.

Puhtaat tilat ($\rho^2=\rho$) ovat ehdon ${\mathrm{tr}\left[{\rho}\right]}=1$ johdosta yksiulotteisia projektioita ja ne määräytyvät vaihetekijää vaille yksikäsitteisistä yksikkövektoreista [1/Taustatietoa 3]. Olkoon $\varphi$ puhdasta tilaa $\rho$ edustava yksikkövektori ($\rho\varphi=\varphi$). Tällöin saadaan $\mathrm{tr}\left[{\rho E}\right]=\left\langle{\varphi}|{E\varphi}\right\rangle$ kaikilla $E\in\boldsymbol{E}$, eli todennäköisyydet $\mathrm{tr}\left[{\rho E}\right]$ voidaan ilmaista myös sisätuloina $\left\langle{\varphi}|{E\varphi}\right\rangle$, joka on sama kaikilla $z\varphi, |z|=1$. Tämän johdosta puhtaat tilat annetaankin usein suoraan yksikkövektoreina ja niitä kutsutaan vektoritiloiksi, tai vain tiloiksi kun asiayhteys on selvä eikä sekaannuksen vaaraa ole.

Tarkalle $\pm 1$-arvoiselle kubittisuureelle käytämme edelleen myös merkintöjä $A=\hat{\boldsymbol{a}}\cdot\boldsymbol\sigma=P_{\hat{\boldsymbol{a}}}-P_{-\hat{\boldsymbol{a}}}$, missä $P_{\pm\hat{\boldsymbol{a}}}=\frac 12(I\pm\hat{\boldsymbol{a}}\cdot\boldsymbol\sigma)$, $\left\|{\hat{\boldsymbol{a}}}\right\|=1$, ja $\boldsymbol\sigma=(\sigma_1,\sigma_2,\sigma_3)$ koostuu Paulin matriiseista

$\;\;\;\;\;\;$$\sigma_1= \left(\begin{matrix} 0& 1 \\ 1&0\end{matrix}\right), \ \sigma_2=\left(\begin{matrix} 0& -\imath \\ \imath&0\end{matrix}\right), \ \sigma_3=\left(\begin{matrix} 1& 0 \\ 0&-1\end{matrix}\right),$

jotka itsessään edustavat kolmea keskeistä kubittisuuretta, spinreaalisaatiossa koordinaattiakselien suuntaisia spinsuureita, fotonireaalisaatiossa polarisaatiosuureita.

Paulin matriiseihin liittyvät kantavektorit, niiden normitetut ominaisvektorit, ovat (vaihetekijää vaille yksikäsitteisesti)

$\;\;\;\;\;\;$$\{\frac 1{\sqrt 2}(1,1)^t,\frac 1{\sqrt 2}(1,-1)^t\}, \ \{\frac 1{\sqrt 2}(1,i)^t,\frac 1{\sqrt 2}(1,-i)^t\},\ \{(1,0)^t,(0,1)^t\},$

jolloin esimerkiksi $P_{\hat{\boldsymbol{x}}}$, $\hat{\boldsymbol{x}}=(1,0,0)$, saadaan vaakavektorin (kompleksikonjugaatin) $\frac 1{\sqrt 2}(1,1)$ ja pystyvektorin $\frac 1{\sqrt 2}(1,1)^t$ Kroneckerin tulona. (Tilasyistä kirjoitamme pystyvektorit vaakavektoreina transpoosia tarkoittavalla yläindeksillä $t$ varustettuina.) $\square$

Oletetaan nyt, että tutkittava fysikaalinen systeemi koostuu kahdesta osasta. Merkitään tätä systeemiä ja sen osia kirjaimilla $\mathcal{S}_{12},\mathcal{S}_1,\mathcal{S}_2$. Yleisen lähestymistapamme puitteissa kutakin näistä kuvataan nyt tila- ja suurejoukoilla $\boldsymbol{S}$ ja $\boldsymbol{O}$ sekä todennäköisyysfunktiolla $p$. Yhdistettyjen systeemien teorian peruskysymys on miten systeemien $\mathcal{S}_{12},\mathcal{S}_1,\mathcal{S}_2$ kuvaukset liittyvät toisiinsa. Erityisesti, jos $\mathcal{S}_1$ ja $\mathcal{S}_2$ ovat kubitteja, Hilbertin avaruuksin $\mathbb C^2$, niin mikä on kubittiparin $\mathcal{S}_{12}$ Hilbertin avaruus ja mitkä ovat sen mahdolliset tilat ja suureet?

Esimerkki 1. Tyypillisessä atomifysiikan kontekstissa esimerkiksi heliumatomi koostuu ytimestä ja kahdesta elektronista, jolloin He-atomi on kolmen systeemin yhdiste, alfahiukkanen ja kaksi elektronia. Ydinfysiikassa alfahiukkanen koostuu kahdesta protonista ja kahdesta neutronista. Hiukkasfysiikan kuuma kysymys on nyt ”mitä protonin sisällä todella on” [2]. Kvanttilaskentaan käytettävissä kvanttiprosessoreissa on päästy testaamaan muutaman kymmenen, jopa yli sadan kubitin verkottumista [3]. $\square$

Yhdistettyjen systeemien kuvauksen intuitiivinen perusajatus voidaan muotoilla seuraavasti:

a) systeemi $\mathcal{S}_{12}$ koostuu systeemeistä $\mathcal{S}_1$ ja $\mathcal{S}_2$, ne voidaan identifioida $\mathcal{S}_{12}$:n osina;

b) systeemit $\mathcal{S}_1$ ja $\mathcal{S}_2$ muodostavat systeemin $\mathcal{S}_{12}$, sillä ei ole muita osia.

Nämä identifioitavuus- ja kattavuusehdot voidaan helposti muotoilla yleisen teorian puitteissa ns. yhdistämissääntöinä. Muotoilemme ne kuitenkin suoraan kvanttimekaniikan Hilbertin avaruus -esityksessä, jonka puitteissa ehdot saavat myös oleellisesti yksikäsitteisen ratkaisunsa. Ehtojen alustavassa muotoilussa ei ole tarpeen spesifioida Hilbertin avaruutta. Olkoot siksi $\mathcal{H}_{12},\mathcal{H}_1,\mathcal{H}_2$ systeemeihin $\mathcal{S}_{12},\mathcal{S}_1,\mathcal{S}_2$ liittyvät Hilbertin avaruudet sekä $\boldsymbol{S}(\mathcal{H}_{12}),\boldsymbol{S}(\mathcal{H}_1),\boldsymbol{S}(\mathcal{H}_2)$ ja $\boldsymbol{E}(\mathcal{H}_{12}),\boldsymbol{E}(\mathcal{H}_1),\boldsymbol{E}(\mathcal{H}_2)$ niiden tila- ja efektijoukot.

Kvanttimekaniikan muotoilu mittaustulostodennäköisyyksien teoriana tarkoittaa, että myös yhdistämissäännöt on perustettava näille todennäköisyyksille. Nämä todennäköisyydet ovat aina muotoa $p^\mathsf{E}_\rho(X)=\mathrm{tr}\left[{\rho\mathsf{E}(X)}\right]$, siis muotoa $\mathrm{tr}\left[{\rho E}\right],\rho\in\boldsymbol{S}, E\in\boldsymbol{E}$. Koska tilat $\rho$ määräytyvät täysin todennäköisyyksistä $\mathrm{tr}\left[{\rho E}\right], E\in\boldsymbol{E},$ ja efektit $E$ (ja siis suureet ja mittaukset) [4] todennäköisyyksistä $\mathrm{tr}\left[{\rho E}\right],\rho\in\boldsymbol{S}$, niin nämä säännöt voidaan muotoilla suoraan joko tilojen tai efektien avulla.

Vaatimus alisysteemin $\mathcal{S}_i, i=1,2,$ identifioitavuudesta $\mathcal{S}_{12}$:n osana voidaan ilmaista vaatimuksena sellaisen injektiivisen (upotus)kuvauksen $\boldsymbol{E}(\mathcal{H}_i)\ni E\mapsto h_i(E)\in\boldsymbol{E}(\mathcal{H})$ olemassaolosta, joka säilyttää efektijoukon $\boldsymbol{E}(\mathcal{H}_i)$ keskeisen rakenteen, kuvaten tarkat efektit tarkoiksi efekteiksi ja säilyttäen efektien yhteismitattavuuden. Jokaista efektiä $E\in\boldsymbol{E}(\mathcal{H}_i)$ kohti on siis oltava olemassa yksikäsitteinen efekti $h_i(E)\in\boldsymbol{E}(\mathcal{H}_{12})$ jonka mittaustulostodennäköisyyksistä efekti $E\in\boldsymbol{E}(\mathcal{H}_i)$ määräytyy. Yhteismitattavuuden säilymisvaatimus takaa muun muassa sen, että jokaista $\mathcal{S}_i$:n suuretta $X\mapsto\mathsf{E}(X)$ vastaa yksikäsitteinen $\mathcal{S}_{12}$:n suure $X\mapsto h_i(\mathsf{E}(X))$ jonka mittaustulostilastoista saadaan suureen $\mathsf{E}$ mittaustulostilastot. Lisäksi on luonnollista vaatia, että ykkösefekti $I\in\boldsymbol{E}(\mathcal{H}_i)$ kuvautuu ykkösefektiksi $h_i(I)=I\in\boldsymbol{E}(\mathcal{H}_{12})$. Identifioitavuusehtoon sisällytetään myös vaatimus, että alisysteemien $\mathcal{S}_1$ ja $\mathcal{S}_2$ efektit $E\in\boldsymbol{E}(\mathcal{H}_1)$ ja $F\in\boldsymbol{E}(\mathcal{H}_2)$ tulkittuna $\mathcal{S}_{12}$:n efekteinä $h_1(E)$ ja $h_2(F)$ voida mitata yhdessä. Erityisesti, suureet $X\mapsto h_1(\mathsf{E}(X))$ ja $Y\mapsto h_2(\mathsf{F}(Y))$ on siis voitava mitata yhdessä.

Kattavuusvaatimus b) on suorimmin ilmaistavissa tiloja koskevana ehtona. Koska puhtaat tilat edustavat maksimaalista tietoa systeemistä, on luonnollista vaatia, että maksimaalinen tieto osasysteemeistä antaa myös täyden tiedon kokonaisuudesta; toisin sanoen, jos sekä $\mathcal{S}_1$ että $\mathcal{S}_2$ ovat puhtaissa tiloissa, niin myös $\mathcal{S}_{12}$ on puhtaassa tilassa.

Edellä kuvatut yhdistämisehdot voidaan ratkaista Hilbertin avaruus -teorian puitteissa [5], jolloin (oleellisesti) yksikäsitteisenä ratkaisuna saadaan, että systeemin $\mathcal{S}_{12}$ Hilbertin avaruus $\mathcal{H}_{12}$ voidaan samastaa systeemien $\mathcal{S}_1$ ja $\mathcal{S}_2$ Hilbertin avaruuksien $\mathcal{H}_1$ ja $\mathcal{H}_2$ (Hilbertin) tensoritulon kanssa, symbolisesti $\mathcal{H}_{12}=\mathcal{H}_1\otimes\mathcal{H}_2$. [6] Tällöin myös systeemin $\mathcal{S}_{12}$ tila- ja efektijoukot ovat $\boldsymbol{S}(\mathcal{H}_{12})=\boldsymbol{S}(\mathcal{H}_1\otimes\mathcal{H}_2)$ ja $\boldsymbol{E}(\mathcal{H}_{12})=\boldsymbol{E}(\mathcal{H}_1\otimes\mathcal{H}_2)$.

Emme tässä paneudu tähän yleiseen teoriaan tämän enempää vaan tyydymme tarkastelemaan kubittiesimerkkiä. Todettakoon kuitenkin, että Hilbertin avaruuksien tensoritulo on assosiatiivinen, jolloin esimerkiksi $\mathcal{H}_1\otimes(\mathcal{H}_2\otimes\mathcal{H}_3)=(\mathcal{H}_1\otimes\mathcal{H}_2)\otimes\mathcal{H}_3$, joten sulut voidaan tässä jättää pois, ja kolmen systeemin $\mathcal{S}_1,\mathcal{S}_2,\mathcal{S}_3$ muodostaman yhdisteen $\mathcal{S}_{123}$ teoria rakentuu Hilbertin avaruudelle $\mathcal{H}_1\otimes\mathcal{H}_2\otimes\mathcal{H}_3$ yleisten periaatteiden mukaisesti. Ei siis ole väliä missä järjestyksessä $\mathcal{S}_{123}$ on kokoonpantu: $\mathcal{S}_{123}=(\mathcal{S}_{12},\mathcal{S}_3)=(\mathcal{S}_1,\mathcal{S}_{23})=(\mathcal{S}_{13},\mathcal{S}_2)$.

2. Kubittipari

Kahden kubitin kvanttimekaniikka rakentuu edellä kuvatun perusteella kubittien Hilbertin avaruuksien $\mathbb{C}^2$ ja $\mathbb{C}^2$ tensoritulolle $\mathbb{C}^2\otimes\mathbb{C}^2$. Vastaavasti $N$:n kubitin teoria pohjautuu kubittiavaruuden $N$-kertaiselle tensoritulolle $\mathbb{C}^2\otimes\ldots\otimes\mathbb{C}^2$. Tässä jaksossa tutustutaan avaruuteen $\mathbb{C}^2\otimes\mathbb{C}^2$ sekä määritetään sille perustuvat tila- ja efektijoukot $\boldsymbol{S}(\mathbb{C}^2\otimes\mathbb{C}^2)$ ja $\boldsymbol{E}(\mathbb{C}^2\otimes\mathbb{C}^2)$. Kirjanpidollisista syistä käytämme tarpeen mukaan geneeristä merkintää $\mathcal{H}_1$ ja $\mathcal{H}_2$ kubittien avaruuksille $\mathbb{C}^2$. Palaamme luvussa 6 lyhyesti kubittien mahdollisesta samanlaisuudesta, identtisyydestä seuraaviin kysymyksiin.

Taustatietoa 1. Hilbertin avaruuksien $\mathcal{H}_1=\mathbb{C}^2$ ja $\mathcal{H}_2=\mathbb{C}^2$, kuten minkä tahansa kahden (tai useamman) äärellisulotteisen vektoriavaruuden, tensoritulo $\mathcal{H}_{12}=\mathbb{C}^2\otimes\mathbb{C}^2$ voidaan muodostaa niiden Kroneckerin tulona,

(2.1) $\;\;\;$$\mathbb{C}^2\times\mathbb{C}^2\ni\left(\left(\begin{matrix} u\\ v\end{matrix}\right),\left(\begin{matrix} z\\ w\end{matrix}\right)\right)\mapsto \left(\begin{matrix} u\\ v\end{matrix}\right)\otimes\left(\begin{matrix} z\\ w\end{matrix}\right)=\left(\begin{matrix} uz\\ uw\\vz\\vw\end{matrix}\right)\in\mathbb{C}^4.$

Helposti todetaan, että tämä kuvaus on bilineaarinen, eli kummankin muuttujan suhteen erikseen lineaarinen. Valitsemalla kummallekin $\mathbb{C}^2$ avaruudelle jokin kanta, saadaan nämä kantavektorit tensoroimalla avaruudelle $\mathbb{C}^4$ kanta. Esimerkiksi, kanonisten kantavektoreiden $(1,0)^t, (0,1)^t$ tensorituloina saadaan $\mathbb{C}^4$:lle kanoninen kanta, vektorit $(1,0,0,0)^t,(0,1,0,0)^t,(0,0,1,0)^t$ ja $(0,0,0,1)^t$.

Jos vektori $\phi\in\mathbb{C}^4$ voidaa lausua muodossa $\phi=\varphi\otimes\psi$ joillekin $\varphi\in\mathcal{H}_1,\psi\in\mathcal{H}_2$, niin sanomme, että $\phi$ on hajoava. Jokainen vektori $\phi\in \mathbb{C}^4$ voidaan lausua hajoavien vektoreiden $\varphi\otimes\psi$ lineaarikombinaatioina, mutta vektori $\phi$ ei tyypillisesti ole hajoava. [7] Tämä ilmeinen mutta tärkeä seikka on kvanttikietoutumisen takana.

Edelleen, helposti todennetaan, että avaruuksien sisätulot ovat yhteensopivat, toisin sanoen

(2.2)$\;\;\;$$\left\langle{\varphi_1}|{\varphi_2}\right\rangle{}_{\mathcal{H}_1}\left\langle{\psi_1}|{\psi_2}\right\rangle_{\mathcal{H}_2}=\left\langle{\varphi_1\otimes\psi_1}|{\varphi_2\otimes\psi_2}\right\rangle{}_{\mathcal{H}_{12}},$

kaikilla vektoreilla $\varphi_1,\varphi_2\in\mathcal{H}_1,\psi_1,\psi_2\in\mathcal{H}_2.\square$

Kahden kubitin Hilbertin avaruuksien tensoritulo $\mathbb{C}^2\otimes\mathbb{C}^2$ on siis $\mathbb{C}^4$. Sama konstruktio saadaan kaikille avaruuksille $\mathbb{C}^n$ ja $\mathbb{C}^m$, $\mathbb{C}^n\otimes\mathbb{C}^m=\mathbb{C}^{nm}$, $n,m\in\mathbb{N}$. Tensoritulon assosiatiivisuudesta saadaan $N$:n kubitin avaruudeksi $N$-kertainen tensoritulo $\mathbb{C}^2\otimes\ldots\otimes\mathbb{C}^2=\mathbb{C}^{2^N}$, joka osoittaa, että avaruuden dimensio kasvaa eksponentiaalisesti kubittilukumäärän mukana.

Taustatietoa 2. Kroneckerin tulo voidaan määritellä myös matriiseille. Esimerkiksi minkä tahansa kahden $2\times 2$ kompleksimatriisin $A=(a_{ij})$ ja $B=(b_{ij})$ Kroneckerin tulo (matriisien tensoritulo) on $4\times 4$ matriisi

$\;\;\;\;\;\;$$A\otimes B=\left(\begin{matrix} a_{11}B& a_{12}B \\ a_{21}B&a_{22}B\end{matrix}\right)= \left(\begin{matrix} a_{11}b_{11}& a_{11}b_{12}&a_{12}b_{11}&a_{12}b_{12} \\ a_{11}b_{21}& a_{11}b_{22}&a_{12}b_{21}&a_{12}b_{22} \\ a_{21}b_{11}& a_{21}b_{12}&a_{22}b_{11}&a_{22}b_{12} \\a_{21}b_{21}& a_{21}b_{22}&a_{22}b_{21}&a_{22}b_{22}\end{matrix}\right).$

Tästä nähdään myös suoraan, että matriisin $A\otimes B$ jälki ${\rm tr}_{\mathcal{H}_{12}}[A\otimes B]$, diagonaalialkioiden summa, on sama kuin matriisien $A$ ja $B$ jälkien ${\rm tr}_{\mathcal{H}_1}[A]$ ja ${\rm tr}_{\mathcal{H}_2}[B]$ tulo, vrt. yhtälö (2.2). Helposti todetaan, että matriisien Kroneckerin tulo on lineaarinen kummankin tekijän suhteen, esim. $(aA+bB)\otimes C=a(A\otimes C)+b(B\otimes C)$. Lisäksi $(A\otimes B)(C\otimes D)=(AC)\otimes(BD)$. Se on myös assosiatiivinen, eli $A\otimes(B\otimes C)=(A\otimes B)\otimes C$, luonnollisesti $8\times 8$ matriisina. $\square$

Kubittiparin $\mathcal{S}_{12}=(\mathcal{S}_1,\mathcal{S}_2)$ tila- ja efektijoukot $\boldsymbol{S}(\mathbb{C}^4)$ ja $\boldsymbol{E}(\mathbb{C}^4)$ voidaan siis antaa $4\times 4$ kompleksimatriiseina, tilat positiivisina jäljen yksi matriiseina, efektit positiivisina ykkösmatriisin rajoittamina matriiseina, siis matriiseina $A\in M(\mathbb{C}^4)$, joille sekä $A$ että $I_4-A$ ovat positiivisia. [8] Tässä $I_4$ on diagonaalimatriisi ${\rm dg}(1,1,1,1)$. Vastaavasti, $I_2={\rm dg}(1,1)$. Merkitsemme kuitenkin jatkossa avaruuksien $\mathcal{H}_{12},\mathcal{H}_1,\mathcal{H}_2$ identiteettikuvausta samalla symbolilla $I$.

Matriisien Kroneckerin tulon avulla voidaan määritellä kuvaukset

$\;\;\;\;\;\;$$\boldsymbol{E}(\mathbb{C}^2)\ni E\mapsto h_1(E)=E\otimes I\in\boldsymbol{E}(\mathbb{C}^4)$

$\;\;\;\;\;\;$$\boldsymbol{E}(\mathbb{C}^2)\ni F\mapsto h_2(F)=I\otimes F\in\boldsymbol{E}(\mathbb{C}^4).$

Helposti nähdään, että nämä kuvaukset ovat alisysteemien identifioitavuusvaatimuksen mukaisia upotuskuvauksia. Lisäksi

$\;\;\;\;\;\;$$h_1(E) h_2(F)=(E\otimes I)(I\otimes F)=E\otimes F=(I\otimes F)(E\otimes I)=h_2(F)h_1(E),$

joten efektit $h_1(E)$ ja $h_2(F)$ kommutoivat keskenään ja ovat siis mitattavissa yhdessä.

Kahden kubitin efektijoukko $\boldsymbol{E}(\mathbb{C}^4)$ sisältää efektien $E\otimes I$ ja $I\otimes F$ lisäksi kaikki (hajoavaa) muotoa $E\otimes F$ olevat efektit, $E\in\boldsymbol{E}(\mathcal{H}_1), F\in\boldsymbol{E}(\mathcal{H}_2)$. On selvää, että kubittiparilla on runsaasti myös muita kuin hajoavia efektejä.

Olkoot $\rho_1\in\boldsymbol{S}(\mathcal{H}_1)$ ja $\rho_2\in\boldsymbol{S}(\mathcal{H}_2)$ mitkä tahansa kaksi tilaa. Niiden tensoritulo $\rho_1\otimes\rho_2$ on kubittiparin mahdollinen tila. Lisäksi jos $\rho_1$ ja $\rho_2$ ovat puhtaita tiloja, niin myös $\rho_1\otimes \rho_2$ on puhdas tila, joka varmistaa, että yhdistämisehto b) toteutuu. Taas on selvää, että hajoavat tilat $\rho_1\otimes\rho_2,\rho_1\in\boldsymbol{S}(\mathcal{H}_1),\rho_2\in\boldsymbol{S}(\mathcal{H}_2)$ ja niiden seokset (konveksikombinaatiot) eivät tyhjennä kubittiparin tilajoukkoa $\boldsymbol{S}(\mathbb{C}^4)$; erityisesti hajoavaa muotoa olevat puhtaat tilat eivät täytä kubittiparin puhtaiden tilojen joukkoa. Tulos on luonnollisesti yhteydessä siihen, että vektori $\phi\in\mathcal{H}_1\otimes\mathcal{H}_2$ ei välttämättä ole hajoava.

Olkoon yhdistetty systeemi tilassa $\rho\in\boldsymbol{S}(\mathcal{H}_{12})$. Alisysteemin $\mathcal{S}_1$ identifioitavuusvaatimuksesta seuraa, että systeemin $\mathcal{S}_1$ on oltava sellaisessa tilassa $\rho_1\in\boldsymbol{S}(\mathcal{H}_1)$, että sen jokaisen suureen $X\mapsto\mathsf{E}(X)$ mittaustulosjakauma tässä tilassa on sama kuin suureen $X\mapsto h_1(\mathsf{E}(X))$ jakauma tilassa $\rho$: kaikilla $\mathsf{E},X$,

(2.3) $\;\;\;$${\rm tr}_{\mathcal{H}_1}[\rho_1\mathsf{E}(X)]= {\rm tr}_{\mathcal{H}_{12}}[\rho h_1(\mathsf{E}(X))] ={\rm tr}_{\mathcal{H}_{12}}[\rho(\mathsf{E}(X)\otimes I)].$

Tämä ehto määrää alisysteemin $\mathcal{S}_1$ tilan yksikäsitteisesti. Vastaava ehto saadaan alisysteemille $\mathcal{S}_2$: kaikilla suureilla $\mathsf{F}$ ja testijoukoilla $Y$,

(2.4) $\;\;\;$${\rm tr}_{\mathcal{H}_2}[\rho_2\mathsf{F}(Y) ]= {\rm tr}_{\mathcal{H}_{12}}[\rho h_2(\mathsf{F}(Y))] = {\rm tr}_{\mathcal{H}_{12}}[\rho(I\otimes\mathsf{F}(Y))].$

Jos yhdistetty systeemi $\mathcal{S}_{12}$ on tilassa $\rho\in\boldsymbol{S}(\mathcal{H}_{12})$, niin alisysteemit ovat välttämättä ehtojen (2.3) ja (2.4) yksikäsitteisesti määrittelemissä tiloissa $\rho_1$ ja $\rho_2$ . Näin määräytyviä kuvauksia $\boldsymbol{S}(\mathcal{H}_{12})\ni\rho\mapsto\rho_i\in\boldsymbol{S}(\mathcal{H}_i)$ kutsutaan osittaisiksi jäljiksi.

On tärkeä huomata, että vaikka $\rho_1\otimes\rho_2\in\boldsymbol{S}(\mathcal{H}_{12})$, niin alisysteemien tilat $\rho_1$ ja $\rho_2$ eivät yleensä riitä määräämään yhdisteen tilaa $\rho$; yleensä $\rho\ne\rho_1\otimes\rho_2$: yhdisteen tilasta määräytyvät alisysteemien tilat muttei yleensä kääntäen. On kuitenkin olemassa tärkeä erikoistapaus, jossa alisysteemien tilat määräävät yhdisteen tilan, tulos joka täydentää yhdistämissäännön b): Puhdas tila $\rho\in\boldsymbol{S}(\mathcal{H}_{12})$ määräytyy yksikäsitteisesti ehtojen (2.3) ja (2.4) määrittelemistä alisysteemien tiloista $\rho_1$ ja $\rho_2$ jos ja vain jos jompi kumpi tiloista $\rho_1$ tai $\rho_2$ on puhdas. Tällöin molemmat alisysteemitilat $\rho_1$ ja $\rho_2$ ovat puhtaita ja $\rho=\rho_1\otimes\rho_2$. Jos $\varphi$ ja $\psi$ ovat tiloja $\rho_1$ ja $\rho_2$ edustavia yksikkövektoreita, niin $\varphi\otimes\psi$ edustaa tilaa $\rho.$ Koska puhdas tila $\rho\in\boldsymbol{S}(\mathcal{H}_{12})$ ei yleensä ole hajoava, siis muotoa $\rho=\rho_1\otimes\rho_2$, niin huomaamme, että yhdistetyn systeemin ollessa puhtaassa tilassa, alisysteemit ovat yleensä sekoitetuissa tiloissa.

Olkoot nyt $\mathsf{E}$ ja $\mathsf{F}$ mitkä tahansa kaksi alisysteemien $\mathcal{S}_1$ ja $\mathcal{S}_2$ suuretta. Niiden määrittelemät yhdistetyn systeemin suureet $X\mapsto h_1(\mathsf{E}(X))$ ja $Y\mapsto h_2(\mathsf{F}(Y))$ ovat keskenään kommutatiivisina yhteismitattavissa ja kaksoissuure $(X,Y)\mapsto \mathsf{E}(X)\otimes\mathsf{F}(Y)$ on niiden eräs yhdistetty suure. Merkitsemme tätä suuretta symbolilla $\mathsf{E}\otimes\mathsf{F}$. [9] Olkoon $\mathcal{S}_{12}$ tilassa $\rho$ ja olkoot $\rho_1$ ja $\rho_2$ vastaavat alisysteemitilat. Todennäköisyysmitat $p^\mathsf{E}_{\rho_1}$ ja $p^\mathsf{F}_{\rho_2}$ ovat yhdistetyn todennäköisyysmitan $p^{\mathsf{E}\otimes\mathsf{F}}_\rho$ marginaalimitat,

$\;\;\;\;\;\;$$p^\mathsf{E}_{\rho_1}(X)=p^{\mathsf{E}\otimes\mathsf{F}}_\rho(X,\Omega_2),\quad p^\mathsf{F}_{\rho_2}(Y)=p^{\mathsf{E}\otimes\mathsf{F}}_\rho(\Omega_1,Y).$

Jos tila $\rho$ on hajoava, $\rho=\rho_1\otimes\rho_2,$ niin $p^{\mathsf{E}\otimes\mathsf{F}}_\rho$ on mittojen $p^\mathsf{E}_{\rho_1}$ ja $p^\mathsf{F}_{\rho_2}$ tulo: $p^{\mathsf{E}\otimes\mathsf{F}}_\rho(X,Y)=p^\mathsf{E}_{\rho_1}(X)p^\mathsf{F}_{\rho_2}(Y)$ kaikilla $X$ ja $Y$. Yleensä näin ei ole ja puhtaan tilan $\rho$ tapauksessa näin on siis vain jos sekä $\rho_1$ että $\rho_2$ ovat myös puhtaita tiloja. Todennäköisyysmitan $p^{\mathsf{E}\otimes\mathsf{F}}_\rho$ poikkeaminen marginaalimittojensa $p^\mathsf{E}_{\rho_1}$ ja $p^\mathsf{F}_{\rho_2}$ tulosta $p^\mathsf{E}_{\rho_1}\times p^\mathsf{F}_{\rho_2}$ on merkki alisysteemien kietoutumisesta toisiinsa tilassa $\rho$.

Huomautus 1. Tässä esitellyt rakenteet, kuten osittaiset jäljet, yleistyvät suoraviivaisesti $N$:n objektin yhdisteille. Esimerkiksi kolmen kubitin tapauksessa yhdisteen tila $\rho\in\boldsymbol{S}(\mathcal{H}_{123})$ määrää kaikki alisysteemitilat $\rho_{12}$, $\rho_{13}$, $\rho_{23}$, $\rho_1$, $\rho_2$, ja $\rho_3$ (ja riippumatta siitä miten esim. alisysteemin $\mathcal{S}_1$ tila määrätään: $\mathcal{S}_{123}=(\mathcal{S}_{12},\mathcal{S}_3)$ =$((\mathcal{S}_1,\mathcal{S}_2),\mathcal{S}_3)$ =$(\mathcal{S}_1,\mathcal{S}_{23})$ =$(\mathcal{S}_1,(\mathcal{S}_2,\mathcal{S}_3))$.) $\square$

Diracin bra- ja ket-symbolit. Kubittiavaruuden $\mathbb{C}^2$ kanoninen kanta $\{(1,0)^t,(0,1)^t\}$ on kubittisuureen $\sigma_3$ ominaiskanta, liittyen sen ominaisarvoihin (mahdollisiin mittaustuloksiin) $\pm 1$. Näitä vektoreita on tapana merkitä myös ns. ket-symboleilla, esim. $|{+}\rangle$ ja $|{-}\rangle$, jolloin vektori $(u,v)^t\in\mathbb{C}^2$ saa muodon $u|{+}\rangle+v|{-}\rangle$. Vastaavasti, $\mathbb{C}^4$:n kanoniset kantavektorit voidaan kirjoittaa muodossa $|{++}\rangle,|{+-}\rangle,|{-+}\rangle,|{- -}\rangle$, missä esim. $|{+-}\rangle=|{+}\rangle\otimes|{-}\rangle$, ja mikä tahansa $\phi\in\mathbb{C}^4$ voidaan näin antaa muodossa $\phi=a|{++}\rangle+b|{+-}\rangle+c|{-+}\rangle+d|{- -}\rangle$, $a,b,c,d\in\mathbb{C}$. Tässä kirjoitustavassa vektori $\phi$ varustetaan myös usein ket-symbolilla, siis kirjoittamalla $|{\phi}\rangle$. Käytämme jatkossa kumpaakin kirjoitustapaa. Tämän merkinnän taustalla on sisätulo $\left\langle{\cdot}|{\cdot}\right\rangle$ ja siitä seuraava matemaattinen tosiasia jonka mukaan jokaisella Hilbertin avaruuden vektorilla $\phi=|{\phi}\rangle$ on yksikäsitteinen duaalivektori, jota merkitään bra-symbolilla $\langle{\phi}|$. Menemättä teknisiin yksityiskohtiin, todettakoon, että mitkä tahansa kaksi vektoria $\phi,\psi\in\mathcal{H}$ määrittelevät yksinkertaisen lineaarisen kuvauksen $|{\phi}\rangle\langle{\psi}|:\mathcal{H}\to\mathcal{H}$ ehdosta $|{\phi}\rangle\langle{\psi}|(\eta)=\left\langle{\psi}|{\eta}\right\rangle\phi$. Kun $\phi=\psi$ ja $\left\|{\phi}\right\|=1$, niin $|{\phi}\rangle\langle{\phi}|$ on yksiulotteinen projektio. Kun $\phi=(a,b,c,d)^t, \psi=(x,y,z,w)^t\in\mathbb{C}^4$, niin lineaarikuvaus $|{\phi}\rangle\langle{\psi}|$ saadaan vektorin $\psi$ transpoosin kompleksikonjugaatin $(\bar x,\bar y,\bar z,\bar w)$ ja vektorin $\phi=(a,b,c,d)^t$ Kroneckerin tulona (huomaa järjestys!). Sisätulon ominaisuuksista seuraa helposti, että jos kirjoitamme $|{\phi}\rangle=\sum_{i,j=\pm}a_{ij}|{ij}\rangle$ ja $|{\psi}\rangle=\sum_{k,l=\pm}b_{kl}|{kl}\rangle$, niin

$\;\;\;\;\;\;$$|{\phi}\rangle\langle{\psi}|=\sum_{ijkl}a_{ij}{\bar b}_{kl}|{ij}\rangle\langle{kl}|,$

missä siis $|{ij}\rangle\langle{kl}|=|{i}\rangle\langle{k}|\otimes|{j}\rangle\langle{l}|$ on kuvaus $\Psi\mapsto\left\langle{kl}|{\Psi}\right\rangle|{ij}\rangle$. Kirjoitustapa tulee erityisen käyttökelpoiseksi kubittiavaruuden dimension $2^N$ kasvaessa; esimerkiksi kolmen kubitin tapauksessa kanoniset kantavektorit ovat $|{ijk}\rangle, i,j,k=\pm$.

Analogisesti bittimerkinnöille, kvanttilaskennassa kubittimallin kantavektoreita $(1,0)^t$ ja $(0,1)^t$ merkitään symboleilla $|0\rangle$ ja $|1\rangle$, kantaa kutsutaan laskennalliseksi kannaksi ja tila $|{0}\rangle$ edustaa laskennan alkutilaa, vastaten bittiä 0. $N$:n bitin merkkijonoja on $2^N$ kappaletta, $00\ldots0,\ldots,11\ldots1$, $N$:n kubitin laskennallinen kanta käsittää yhtä monta kantavektoria, $|{00\ldots 0}\rangle,\ldots,|{11\ldots 1}\rangle$, ja lisäksi jatkumon verran niiden superpositioita. Juuri tämä lisä on kvanttilaskennan taustalla. $\square$

Esimerkki 2. Olkoon $A=\hat{\boldsymbol{a}}\cdot\boldsymbol\sigma=P_{\hat{\boldsymbol{a}}}-P_{-\hat{\boldsymbol{a}}}$ ja $B=\hat{\boldsymbol{b}}\cdot\boldsymbol\sigma=P_{\hat{\boldsymbol{b}}}-P_{-\hat{\boldsymbol{b}}}$, jolloin

$\;\;\;\;\;\;$$A\otimes B=P_{\hat{\boldsymbol{a}}}\otimes P_{\hat{\boldsymbol{b}}}-P_{\hat{\boldsymbol{a}}}\otimes P_{-\hat{\boldsymbol{b}}}-P_{-\hat{\boldsymbol{a}}}\otimes P_{\hat{\boldsymbol{b}}}+P_{-\hat{\boldsymbol{a}}}\otimes P_{-\hat{\boldsymbol{b}}},$

joka on suureen $A\otimes B$ mahdollisiin mittaustulospareihin (1,1), (1,-1), (-1,1) ja (-1,-1) liittyvä hajotelma. Bra- ja ket-merkintöihin viitaten, esimerkiksi yksiulotteinen projektio $P_{\hat{\boldsymbol{a}}}$ voidaan lausua muodossa $|{\varphi_{\hat{\boldsymbol{a}}}}\rangle\langle{\varphi_{\hat{\boldsymbol{a}}}}|$, missä esim. $\varphi_{\hat{\boldsymbol{a}}}=\left(\sqrt{\frac12(1+a_3)}),\frac 12(a_1+\imath a_2)/\sqrt{\frac 12(1+a_3)}\right)^t$ [1/Taustatietoa 3]. [10] Vastaavasti, esim. $P_{-\hat{\boldsymbol{b}}}=|{\varphi_{-\hat{\boldsymbol{b}}}}\rangle\langle{\varphi_{-\hat{\boldsymbol{b}}}}|$, jolloin voidaan todeta, että esim.

$\;\;\;\;\;\;$$P_{\hat{\boldsymbol{a}}}\otimes P_{-\hat{\boldsymbol{b}}}=|{\varphi_{\hat{\boldsymbol{a}}}}\rangle\langle{\varphi_{\hat{\boldsymbol{a}}}}|\otimes |{\varphi_{-\hat{\boldsymbol{b}}}}\rangle\langle{\varphi_{-\hat{\boldsymbol{b}}}}|=|{\varphi_{\hat{\boldsymbol{a}}}\otimes \varphi_{-\hat{\boldsymbol{b}}}}\rangle\langle{\varphi_{\hat{\boldsymbol{a}}} \otimes \varphi_{-\hat{\boldsymbol{b}}}}|.\;\;\;\square$

3. Kvanttikietoutuminen

Kvanttikietoutuminen tai lomittuminen on kvanttimekaniikan yksi merkittävimmistä erityispiirteistä: jopa kaukana toisistaan olevat systeemit voivat olla toisiinsa vahvasti tilastollisesti kytkeytyneitä ilman, että niiden välillä vallitsee mitään vuorovaikutusta; se mitä kietoutuneen parin toiselle jäsenelle tehdään, voi ikään kuin vaikuttaa (ilman vuorovaikutusta!) etäällä olevaan parin toiseen jäseneen. Tämä klassisesta fysiikasta tuntematon, arkikokemuksen vastainen piirre on yksi kvanttimekaniikan tulkintakiistoja eniten aiheuttaneista teorian ominaisuuksista. Samalla siitä on muodostunut merkittävä uusi voimavara kvanttimekaniikan informaatioteoreettisille sovelluksille.

Vaikka kietoutuneiden kubittiparien tuottaminen onkin jo arkirutiinia jopa hyvin varustetuissa opetuslaboratorioissa ja tällaisia pareja osataan tuottaa kontrolloidusti jopa sateliittietäisyyksillä, [11] niin ilmiön esiintuoma kvanttimekaniikan erityinen epälokaalisuus on ajatusta yhä hämmentävä seikka.

Ongelmalla on melko pitkä, tieteenfilosofisestikin varsin mielenkiintoinen historiansa. Sen alku sijoitetaan yleensä vuoteen 1935, jolloin kvanttimekaniikan alkuvuosien pääkriitikko Albert Einstein konstruoi yhdessä Boris Podolskyn ja Nathan Rosenin kanssa ensimmäisen esimerkkihahmotelman tällaisesta hiukkasparista. [12] Tämän innoittamana Erwin Schrödinger julkaisi vielä samana vuonna aihepiiristä kaksi matemaattisesti täsmällisempää ja laajempaa tutkimusta [13], joiden vaikutus jäi kuitenkin vielä tuolloin melko vähäiseksi Niels Bohrin `kumottua’ Einsteinin, Podolskyn ja Rosenin johtopäätöksen. [14]

Einstein, Podolsky ja Rosen (EPR) käyttivät esimerkkiään osoittaakseen, että kvanttimekaniikan antama kuva fysikaalisesta todellisuudesta on epätäydellinen, aihepiiri, jota myös Schrödinger kirjoituksissaan sivusi. Tämä ns. EPR-epätäydellisyysargumentti säilyi kuitenkin eräänlaisena juupas-eipäs-kysymyksenä 1960-luvun alkupuolelle asti, jolloin John Bellin johtamat epäyhtälöt, ns. Bellin epäyhtälöt, osoittivat, että Einsteinin, Podolskyn ja Rosenin päättely rakentui keskenään ristiriitaisille olettamuksille. [15] Bellin epäyhtälöt luonnehtivat tietyn tyyppisiä realistis-lokaalisia teorioita, joiden mittaustulosennusteet poikkeavat tietyissä äärimmäisissä tilanteissa kvanttimekaniikan ennusteista; palaamme tähän lyhyesti luvussa 4. Bellin tulokset ja niiden edelleen kehittelyt puolestaan johtivat muutaman vuosikymmenen mittaiseen äärimmäisen haastavaan kokeelliseen tutkimukseen kvanttimekaniikan ja realistis-lokaalisten teorioiden välisestä kiistasta, joka vuosituhannen vaihteeseen mennessä oli tiedeyhteisön vallalla olevan käsityksen mukaan ratkennut kvanttimekaniikan hyväksi. Näiden tutkimusten myötä yksittäisten kvanttiobjektien manipulointi, kontrollointi, ja toisiinsa kytkeminen on kehittynyt orastavaksi kvanttiteknologiaksi, jossa kvanttikietoutuminen on keskeinen uusi resurssi.

*****

Yhdistetyn systeemin $\mathcal{S}_{12}=(\mathcal{S}_1,\mathcal{S}_2)$ tilat, ja erityisesti sen puhtaat tilat eivät välttämättä ole tulomuotoa. Tämä johtuu siitä matemaattisesta tosiasiasta, että Hilbertin tensoritulo $\mathcal{H}_1\otimes\mathcal{H}_2$ muodostuu tulomuotoa olevien vektorien $\varphi\otimes\psi$ lineaarikombinaatioista, [16] tensoritulo ei ole karteesinen tulo: jokainen $\phi\in\mathcal{H}_{12}$ voidaan lausua muodossa $\sum_{ij}c_{ij}\varphi_i\otimes\psi_j$, joillekin $c_{ij}\in\mathbb{C}, \varphi_i\in\mathcal{H}_1,\psi_j\in\mathcal{H}_2$, mutta sitä ei välttämättä voida esittää muodossa $\varphi\otimes\psi$ millekään $\varphi\in\mathcal{H}_1,\psi\in\mathcal{H}_2$. Tästä aiheutuvaa alisysteemien keskinäistä tilastollista riippuvuutta kutsutaan kvanttikietoutumiseksi tai lomittumiseksi. Ilmiö on läheisessä yhteydessä puhtaiden tilojen superponoitumiseen.

Sanomme, että puhdas tila on (kvantti)kietoutunut, tai lomittunut, jos se ei ole hajoava. Yleisemmin, tila $\rho\in\boldsymbol{S}(\mathcal{H}_{12})$ on separoituva jos se voidaan esittää hajoavien tilojen seoksena, siis muodossa

$\;\;\;\;\;\;$$\rho=\sum_i \lambda_i\rho_1^i\otimes\rho_2^i, \qquad \lambda_i\geq 0, \sum \lambda_i=1, \rho_1^i\in\boldsymbol{S}(\mathcal{H}_1), \rho_2^i\in\boldsymbol{S}(\mathcal{H}_2).$

Jos tila $\rho$ ei ole separoituva, se on kietoutunut. Kietoutuminen määritellään siis negaation kautta ja sen yhteydessä puhutaan usein myös ei-klassisista korrelaatioista.

Tyydymme tässä tarkastelemaan vain puhtaiden tilojen kietoutumista, ja sitäkin pääasiassa vain kubittiparien tapauksessa. Kietoutumiskäsite yleistyy kuitenkin luonnollisella tavalla useammalle systeemille. Esimerkiksi kolmen systeemin yhdisteen tila $\rho\in\boldsymbol{S}(\mathcal{H}_{123})$ voi olla täysin, osittain, tai ei lainkaan kietoutunut, riippuen siitä onko se esim. muotoa $\rho=\rho_{12}\otimes\rho_3$ vai ei, vrt. Huomautus 1 ja Esimerkki 3. Käytämme edelleen geneerisiä merkintöjä tilanteissa joissa tulokset ovat yleisiä.

Tilan $\rho\in\boldsymbol{S}(\mathcal{H}_{12})$ kietoutuminen ilmenee siinä, että joidenkin alisysteemisuureiden $\mathsf{E}$ ja $\mathsf{F}$ yhteismittaustulosjakaumia $p^{\mathsf{E}\otimes\mathsf{F}}_\rho$ ei saada tulomuodossa $p^\mathsf{E}_{\rho_1}\times p^\mathsf{F}_{\rho_2}$ (eikä tällaisten mittojen konveksikombinaatioina). Yhdistetyn mitan poikkeamaa marginaalimittojensa tulosta voidaan mitata monella tavalla, esimerkiksi ns. normitetulla korrelaatiokertoimella, joka on luku välillä $[-1,1]$, ääripäiden edustaessa vahvaa (negatiivista tai positiivista) korrelaatiota. [17] Jos tila ei ole kietoutunut, eli on hajoava, niin korrelaatio on nolla. Voidaan osoittaa, että puhdas tila on kietoutunut jos ja vain jos on olemassa ainakin yksi pari tässä tilassa vahvasti korreloivia alisysteemisuureita. Kietoutumisen asteesta riippuen tällaisia pareja voi olla yksi tai useampi, jopa ääretön määrä.

Taustatietoa 3. Jokainen yhdisteen $\mathcal{S}_{12}$ vektoritila $\phi\in\mathcal{H}_1\otimes\mathcal{H}_2$ voidaan esittää (superpositiona) muodossa

(3.1)$\;\;\;$$\phi=\sum_i\lambda_i\varphi_i\otimes\psi_i,$

missä vektorijonot $(\varphi_i)\subset\mathcal{H}_1$ ja $(\psi_i)\subset\mathcal{H}_2$ (äärellisiä tai äärettömiä [18]) koostuvat keskenään kohtisuorista yksikkövektoreista (vektoritiloista), kukin $\lambda_i>0,$ ja $\sum_i\lambda_i^2=1$. Tämä erityinen lineaarikombinaatio on ns. Schmidtin hajotelma. Jos jonoissa on vain yhdet vektorit, niin tila on hajoava.

Kubittiparin $\mathcal{S}_{12}$ tapauksessa hajotelmasta seuraa, että jokainen kietoutunut vektoritila voidaan antaa muodossa

(3.2)$\;\;\;$$\phi=\lambda_1\varphi_1\otimes\psi_1+\lambda_2\varphi_2\otimes\psi_2,$

missä $\lambda_1,\lambda_2>0$, $\lambda_1^2+\lambda_2^2=1$, ja vektorit $\varphi_1,\varphi_2\in\mathcal{H}_1=\mathbb{C}^2$ ja $\psi_1,\psi_2\in\mathcal{H}_2=\mathbb{C}^2$ ovat keskenään kohtisuoria yksikkövektoreita, $\left\langle{\varphi_i}|{\varphi_j}\right\rangle_{\mathcal{H}_1}=\delta_{ij}$ ja $\left\langle{\psi_i}|{\psi_j}\right\rangle_{\mathcal{H}_2}=\delta_{ij}$. Alisysteemitilat ovat välttämättä sekoitettuja tiloja,

$\;\;\;\;\;\;$$\rho_1=\lambda_1^2|{\varphi_1}\rangle\langle{\varphi_1}|+\lambda_2^2|{\varphi_2}\rangle\langle{\varphi_2}|, \qquad \rho_2=\lambda_1^2|{\psi_1}\rangle\langle{\psi_1}|+\lambda_2^2|{\psi_2}\rangle\langle{\psi_2}|.$

Kääntäen, mitkä tahansa kaksi (ortonormaalia) kantaa $\{\varphi_1,\varphi_2\}\subset\mathcal{H}_1=\mathbb{C}^2$ ja $\{\psi_1,\psi_2\}\subset\mathcal{H}_2=\mathbb{C}^2$ ja mitkä tahansa kaksi positiivilukua $\lambda_1\ne 0\ne \lambda_2$, joille $\lambda_1^2+\lambda_2^2=1$, määrittelevät kubittiparin erään kietoutuneen tilan ja tässä tilassa suureiden $A=|{\varphi_1}\rangle\langle{\varphi_1}|-|{\varphi_2}\rangle\langle{\varphi_2}|$ ja $B= |{\psi_1}\rangle\langle{\psi_1}|-|{\psi_2}\rangle\langle{\psi_2}|$ mittaustulostodennäköisyydet korreloivat vahvasti. Huomaa, että jos (3.2) on tilojen $\varphi_1\otimes\psi_1$ ja $\varphi_2\otimes\psi_2$ tasavahva superpositio, eli $\lambda_1=\lambda_2$, niin $\rho_1=\rho_2=\frac 12 I$, joka on maksimaalisesti sekoitettu tila (antaen kaikille suureille vakiojakauman).

Vektoritilan $\psi\in\mathcal{H}_1\otimes\mathcal{H}_2$ tapauksessa kietoutumiselle ja sen asteelle on Schmidtin hajotelman johdosta selkeä matemaattinen luonnehdinta. Sen sijaan kysymys annetun tilan, puhdas tai sekoitettu, mahdollisen kietoutumisen operationaalinen karakterisointi (mittaustulostilastojen avulla) on hyvin vaativa ja vain osittain ratkaistu kysymys. Palaamme tähän seuraavassa jaksossa. $\square$

Vaikka edeltävä esimerkki onkin kattava kubittiparin kietoutuneiden puhtaiden tilojen rakenteen esittelyn kannalta, on hyödyllistä tarkastella erikseen kanonisten kantavektoreiden $|{+}\rangle,|{-}\rangle$ avulla määriteltyjä kietoutuneita tiloja. Kun vielä valitsemme superposition (3.2) tasavahvaksi ja kiinnitämme sopivat vaihetekijät, saamme seuraavat neljä keskenään kohtisuoraa yksikkövektoria, ns. Bellin vektorit,

(3.3)$\;\;\;$$\Phi^{\pm}=\frac 1{\sqrt 2}(|{++}\rangle\pm|{- -}\rangle),$

(3.4)$\;\;\;$$\Psi^{\pm}=\frac 1{\sqrt 2}(|{+-}\rangle\pm|{-+}\rangle).$

Kussakin tapauksessa alisysteemitilat ovat maksimaalisesti sekoitettuja.

Olkoot $A=\hat{\boldsymbol{a}}\cdot\boldsymbol\sigma=P_{\hat{\boldsymbol{a}}}-P_{-\hat{\boldsymbol{a}}}$ ja $B=\hat{\boldsymbol{b}}\cdot\boldsymbol\sigma=P_{\hat{\boldsymbol{b}}}-P_{-\hat{\boldsymbol{b}}}$ , jolloin kummallekin suureelle molemmat mittaustulostodennäköisyydet ovat näissä tiloissa $\frac 12$ ja siis $p^A_{\rho_1}(\{k\})p^B_{\rho_2}(\{l\})=\frac 14$, kaikilla $k,l=\pm 1$. Sen sijaan kaikki todennäköisyydet $p^{A\otimes B}_{\Phi^\pm}(\{k,l\})$ ja $p^{A\otimes B}_{\Psi^\pm}(\{k,l\})$ ovat epätriviaaleja ja riippuvat suunnista $\hat{\boldsymbol{a}}$ ja $\hat{\boldsymbol{b}}$, paitsi kun $\hat{\boldsymbol{a}}\perp\hat{\boldsymbol{b}}$. Nämä voidaan helposti laskea, esimerkiksi

(3.5)$\;\;\;$$p^{A\otimes B}_{\Psi^-}(\pm 1,\pm 1) = \frac{1}{4}(1-\hat{\boldsymbol{a}}\cdot\hat{\boldsymbol{b}})=\frac{1}{2} \sin^2 \frac{\theta_{\boldsymbol{a},\boldsymbol{b}}}{2},$

(3.6)$\;\;\;$$p^{A\otimes B}_{\Psi^-}(\pm 1,\mp 1) =\frac{1}{4}(1+\hat{\boldsymbol{a}}\cdot\hat{\boldsymbol{b}})=\frac{1}{2} \cos^2 \frac{\theta_{\boldsymbol{a},\boldsymbol{b}}}{2}.$

Tässä on erityisen huomionarvoista se, että jos $A=B$, eli kummaltakin osasysteemiltä mitataan sama suure, niin mahdollisista neljästä mittaustulosparista $(1,1), (1,-1), (-1,1), (-1,-1)$ vain kaksi, $(1,-1)$ ja $(-1,1)$, ovat nyt mahdollisia, ja kummatkin todennäköisyydellä $\frac 12$; suureparin $(A,A)$ välillä on vahva (negatiivinen) korrelaatio tilassa $\Psi^-$ olipa suunta $\hat{\boldsymbol{a}}$ mikä tahansa. Lisäksi on syytä korostaa, että nämä tilat eivät riipu kubittien avaruudellisesta asemasta, niiden keskinäinen etäisyys ei vaikuta asiaan. Edelleen, kubittien välillä ei tarvitse olla minkäänlaista vuorovaikutusta, ne voivat olla dynaamisesti riippumattomia mutta ovat tilastollisesti vahvasti toisiinsa kytkeytyneitä.

Huomautus 2. Kietoutuneita kubittipareja, ja yleisemminkin kietoutuneita objektipareja voidaan tuottaa monella eri tavalla, tyypillisesti sopivien lyhytaikaisten vuorovaikutusten avulla tai vaikkapa spontaaneissa (tai stimuloiduissa) hajoamisprosesseissa kuten atomien viritystilojen purkautuessa. Yleisimmin käytössä olevat lähteet tuottavat polarisaatiokietoutuneita fotonipareja. Tällaisten fotoniparien tuottamiseen käytetään usein fysikaalista prosessia, jota kutsutaan tyypin II spontaaniksi parametriseksi alaskäännöksi (type II spontaneous parametric down conversion). Tämä prosessi tapahtuu, kun ns. pumppulaserilla tuotettu lineaarisesti polarisoitu valo (laserpulssi) johdetaan epälineaariseen kiteeseen. Prosessissa yksi fotoni voi spontaanisti muuntua kahdeksi fotoniksi, joilla on vastakkaiset polarisaatiot. Energian säilymislain nojalla $\omega_0= \omega_1 + \omega_2$, missä $\omega_0$ on alkuperäisen fotonin energia ja $\omega_1$ ja $\omega_2$ ovat syntyneiden fotonien energiat. Erityisesti prosessissa voi syntyä fotonipareja, joiden energia on puolet alkuperäisen fotonin energiasta, $\omega_1 = \omega_2 = \omega_0/2$. Koska lisäksi impulssin säilymislaki on voimassa, niin syntyneet fotonit emittoituvat eri kartioihin. Kiteen kahtaistaittavuudesta johtuen kartioiden suuntia voidaan muuttaa. Erityisesti kartiot saadaan leikkaamaan toisensa, jolloin fotonipareja voidaan kerätä kartioiden leikkauskohdista, kuva 1, joista fotonit ohjataan optisille kuiduille ja erilaisten optisten laitteiden läpi mittausasemille, kuva 2. Kunkin fotoniparin yksittäiset fotonit ovat erottautumattomat lukuunottamatta niiden polarisaatiovapausastetta. Vaikka osoittautuukin, että näin voidaan tuottaa mm. Bellin tiloilla kuvattavissa olevia polarisaatiokietoutuneita fotonipareja, niin fotoniparin tilan tosiallinen määritys mittaustulosdatasta on erityisen haastava ja se voidaan ratkaista vain kokeellisesti. $\square$

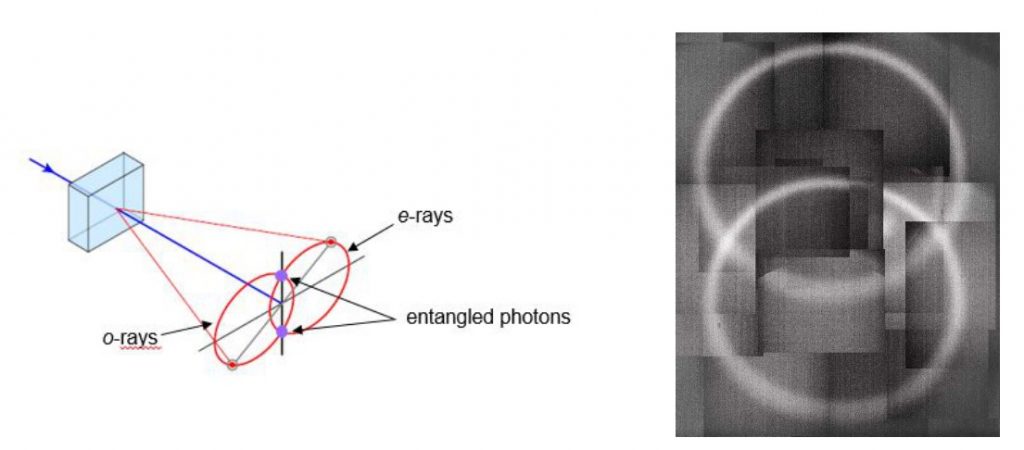
Kuva 1. Polarisaatiokietotuneiden fotoniparien tuottaminen: kaaviokuvassa BBO kide ja syntyvät valokartiot, vieressä kuvan 2 laitteistolla saatu tosiasiallinen (osakuvista rekonstruoitu) kartioleikkaus.

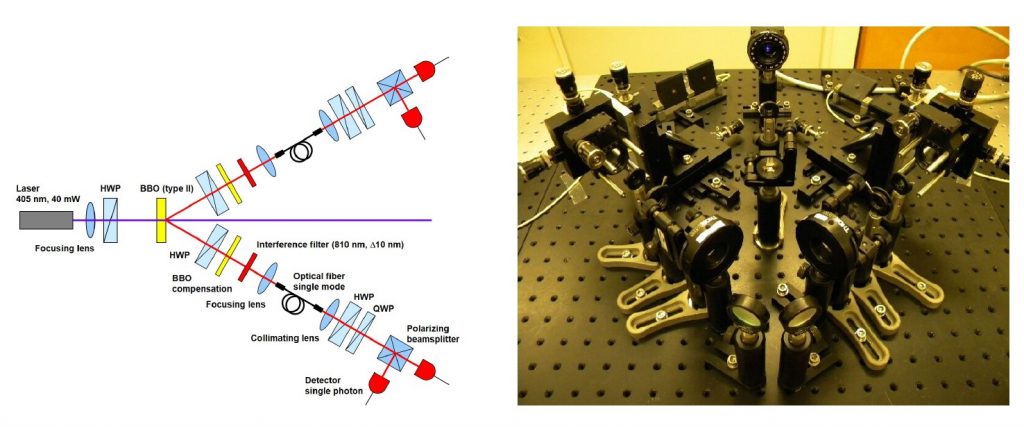
Kuva 2. Polarisaatiokietotuneiden fotoniparien tuottaminen: kaaviokuvassa tilan määritykseen tarvittavaa optiikkaa, vieressä Turun yliopiston kvanttioptiikan laboratorion laitteisto.

Huomautus 3. Kietoutuneita pareja syntyy yleensä sopivan vuorovaikutuksen tuloksena. Kietoutuneita tiloja voidaan kuitenkin tuottaa myös ilman, että osasysteemit ovat koskaan vuorovaikuttaneet keskenään. Palaamme tähän jaksossa 5.2. $\square$

Esimerkki 3. Kolmen kubitin tärkeitä kietoutuneita tiloja ovat ns. GHZ- ja W-tilat,

(3.7)$\;\;\;$$|{GHZ}\rangle=\frac 1{\sqrt 2}(|{+++}\rangle+|{- – -}\rangle),$

(3.8)$\;\;\;$$|{W}\rangle=\frac 1{\sqrt 3}(|{+- -}\rangle+|{-+-}\rangle+|{- -+}\rangle).$

Näillä tiloilla on merkittäviä eroja kun tarkastellaan niiden yhtälöistä (2.3)-(2.4) määräytyviä alisysteemitiloja. Esimerkiksi tila

$\;\;\;\;\;\;$$\rho_{12}^{|{GHZ}\rangle}=\frac 12|{++}\rangle\langle{++}|+\frac 12|{- -}\rangle\langle{- -}|$

on separoituva tila, kun taas tila

$\;\;\;\;\;\;$$\rho_{12}^{|{W}\rangle}=\frac 13(|{+-}\rangle\langle{+-}|+|{-+}\rangle\langle{+-}|+|{+-}\rangle\langle{-+}|+|{-+}\rangle\langle{-+}|+|{- -}\rangle\langle{- -}|),$

on edelleen kietoutunut (sekoitettu) tila. $\square$

4. Kvanttikietoutuminen ja Bellin epäyhtälöt

Kvanttikietoutuminen on läheisessä yhteydessä ns. Bellin epäyhtälöihin, niiden rikkoutumiseen. Näille matemaattisesti melko yksinkertaisille epäyhtälöille on esitetty monia vaihtoehtoisia johtoja ja muotoiluja. Tämä moninaisuus johtuu siitä, että nämä epäyhtälöt luonnehtivat tietyn tyyppisiä fysikaalisia teorioita, joiden käsitteellinen lähtökohta vaihtelee valituista ennakkoehdoista sekä tieteenfilosofisista näkökulmista riippuen. Esittelemme tässä pääpiirteittäin Bellin epäyhtälöiden klassisen (Kolmogorovin) todennäköisyysteoreettisen muotoilun sekä Einsteinin, Podolskyn ja Rosenin artikkelin pohjalta rakentuvan muotoilun. Alan kirjallisuus on varsin laaja. Google Scholar antaa noin 935 000 tulosta hakusanalle Bell inequality, noin 88 400 tulosta sanalle quantum nonlocality, sanalle EPR argument noin 47 900 tulosta, ja sanalle quantum entanglement noin 359 000 tulosta (haettu 7.4.2021), joten aihepiirin tyhjentävä analyysi ei enää ole mahdollista.

4.1 Epäyhtälöiden todennäköisyysteoreettinen muotoilu

Todennäköisyyksien korrelaatiot ovat tuttuja myös klassisista teorioista. Kvanttimekaniikassa mahdollisten mittaustulosten välinen korrelaatio, probabilistinen riippuvuus, voi kuitenkin olla klassisesta teoriasta poikkeavaa. Tämä seikka on tullut epäsuorasti esille jo yhteismitattavuuden problematiikan yhteydessä [1], jossa nähtiin, että kahden kaksiarvoisen todennäköisyysmitan $\mu=p^A_{\rho_{\boldsymbol{n}}}$ ja $\nu=p^B_{\rho_{\boldsymbol{n}}}$, $A=P_{\hat{\boldsymbol{a}}}-P_{-\hat{\boldsymbol{a}}}$, $B=P_{\hat{\boldsymbol{b}}}-P_{-\hat{\boldsymbol{b}} }$, $\rho_{\hat{\boldsymbol{n}}}\in\boldsymbol{S}(\mathbb{C}^2)$, mikään yhdistetty mitta $\gamma_r$ [19] ei voi kuvata suureisiin $A$ ja $B$ liittyviä paritodennäköisyyksiä elleivät $A$ ja $B$ kommutoi keskenään. Bellin epäyhtälöt luonnehtivat klassisesti yhteensopivia paritodennäköisyyksiä, siis paritodennäköisyyksiä jotka saadaan jostakin yhdistetystä todennäköisyysmitasta. Bellin epäyhtälöiden rikkoutuminen on siksi merkki ei-klassisista korrelaatioista eli kvanttikietoutumisesta.

Tarkastellaan kubittiparia $\mathcal{S}_{12}$ ja sen neljää osasysteemisuuretta $A,A’$ ja $B,B’$, liittyen kubitteihin $\mathcal{S}_1$ ja $\mathcal{S}_2$, vastaavasti. [20] Näihin suureisiin ja suurepareihin $A\otimes B,A’\otimes B, A\otimes B’, A’\otimes B’$ liittyvät mittaustulostodennäköisyydet ovat hyvin määriteltyjä missä tahansa yhdisteen tilassa $\rho$ ja ne voidaan konstruoida kokeellisesti neljässa erillisessä koejärjestelyssä. Merkitään kyllä ja kyllä-kyllä -tuloksiin liittyviä todennäköisyyksiä lyhyesti symboleilla $p(a),\ldots,p(a’,b’)$, missä esimerkiksi $p(b)=\mathrm{tr}[{\rho I\otimes P_{\hat{\boldsymbol{b}}}}]$ ja $p(a’,b)=\mathrm{tr}[{\rho P_{\hat{\boldsymbol{a}}’}\otimes P_{\hat{\boldsymbol{b}}}}]$. Tällöin esimerkiksi $1-p(a)=\mathrm{tr}[{\rho P_{-\hat{\boldsymbol{a}}}\otimes I}]$ on kyseisen mittauksen ei -tuloksen todennäköisyys tilassa $\rho$. Sanomme, että todennäköisyyssysteemi

$\;\;\;\;\;\;$$K=\{p(a),p(a’),p(b),p(b’);p(a,b),p(a,b’),p(a’,b), p(a’,b’)\}$

on klassisesti esitettävissä, jos on olemassa klassinen (Kolmogorovin) todennäköisyysmitta, josta nämä luvut saadaan. [21] Voidaan osoittaa, että lukukahdeksikko $K$ on klassisesti esitettävissä tarkalleen silloin kun seuraavat epäyhtälöt ovat voimassa: [22] kaikilla $x=a,a’,y=b,b’$,

(4.1)$\;\;\;$$0\leq p(x,y)\leq p(x)\leq 1,\; 0\leq p(x,y)\leq p(y)\leq 1,\; p(x)+p(y)-p(x,y)\leq 1,$

(4.2)$\;\;\;$$0\leq p(a)+p(b’)-p(a,b)-p(a,b’)-p(a’,b’)+p(a’,b)\leq 1,$

(4.3)$\;\;\;$$0\leq p(a’)+p(b’)-p(a’,b)-p(a’,b’)-p(a,b’)+p(a,b)\leq 1,$

(4.4)$\;\;\;$$0\leq p(a)+p(b)-p(a,b’)-p(a,b)-p(a’,b)+p(a’,b’)\leq 1,$

(4.5)$\;\;\;$$0\leq p(a’)+p(b)-p(a’,b’)-p(a’,b)-p(a,b)+p(a,b’)\leq 1.$

Kahdeksaa epäyhtälöä (4.2)- (4.5) kutsutaan usein Bellin tai Clauser-Horne-Shimony-Holt (CHSH) epäyhtälöiksi. Niille on esitetty myös useita vaihtoehtoisia muotoiluja ja todistuksia. Näistä huomattavin on ns. lokaali klassinen malli, jossa otetaan eksplisiittisesti huomioon systeemin jako osasysteemeihin.

Olkoon $\rho$ mikä tahansa Bellin tiloista; esimerkiksi vektoritila $\Psi^-$, jolloin $p(a)=p(a’)=p(b)=p(b’)=\frac 12$ ja paritodennäköisyydet saadaan yhtälöistä (3.5) – (3.6). Epäyhtälöt (4.2)-(4.6) saadaan nyt muotoon

$\begin{eqnarray*}-2&\leq& \hat{\boldsymbol{a}}\cdot\hat{\boldsymbol{b}}+\hat{\boldsymbol{a}}\cdot\hat{\boldsymbol{b}}’+\hat{\boldsymbol{a}}’\cdot\hat{\boldsymbol{b}}’-\hat{\boldsymbol{a}}’\cdot\hat{\boldsymbol{b}}\leq 2,\\-2&\leq& \hat{\boldsymbol{a}}’\cdot\hat{\boldsymbol{b}}+\hat{\boldsymbol{a}}’\cdot\hat{\boldsymbol{b}}’+\hat{\boldsymbol{a}}\cdot\hat{\boldsymbol{b}}’-\hat{\boldsymbol{a}}\cdot\hat{\boldsymbol{b}}\leq 2,\\-2&\leq& \hat{\boldsymbol{a}}\cdot\hat{\boldsymbol{b}}’+\hat{\boldsymbol{a}}\cdot\hat{\boldsymbol{b}}+\hat{\boldsymbol{a}}’\cdot\hat{\boldsymbol{b}}-\hat{\boldsymbol{a}}’\cdot\hat{\boldsymbol{b}}’\leq 2,\\-2&\leq& \hat{\boldsymbol{a}}’\cdot\hat{\boldsymbol{b}}’+\hat{\boldsymbol{a}}’\cdot\hat{\boldsymbol{b}}+\hat{\boldsymbol{a}}\cdot\hat{\boldsymbol{b}}-\hat{\boldsymbol{a}}\cdot\hat{\boldsymbol{b}}’\leq 2,\end{eqnarray*}$

joka osoittaa, että näiden todennäköisyyksien klassinen esitettävyys asettaa voimakkaita rajoituksia suureille $A,A’,B,B’$. Jo yhdenkin epäyhtälön rikkoutuminen estää klassisen esitettävyyden. Helposti voidaan varmistaa, että epäyhtälöt rikkoutuvat esimerkiksi suuntavalinnoilla $\hat{\boldsymbol{a}}\cdot\hat{\boldsymbol{b}}$ = $\hat{\boldsymbol{a}}’\cdot\hat{\boldsymbol{b}}$ = $\hat{\boldsymbol{a}}’\cdot\hat{\boldsymbol{b}}’$ = $\cos\frac\pi{8}$ = $\frac 12\sqrt{2+\sqrt 2}$ ja $\hat{\boldsymbol{a}}\cdot\hat{\boldsymbol{b}}’$ = $\cos\frac{3\pi}8$=$\frac 12\sqrt{2-\sqrt 2}$. Tämä osoittaa, että kvanttimekaniikan mukaan on olemassa hyvin määriteltyjä, kokeellisesti todennettavissa olevia tapahtumia, joihin liittyviä mittaustulostodennäköisyyksiä klassinen teoria ei pysty selittämään. Hajoavaan (ja yleisemmin separoituvaan) tilaan liittyvät todennäköisyydet toteuttavat ylläolevaa muotoa oleviin lokaalisiin mittauksiin liittyvät Bellin epäyhtälöt, joten Bellin epäyhtälöiden rikkoutuminen on merkki kietoutumisesta. [23]

4.2 EPR argumentti

Einstein, Podolsky ja Rosen perustivat päättelynsä kvanttimekaniikan epätäydellisyydestä konstruoimalla esimerkin vuorovaikutuksettomasta systeemiparista, joka nykytermein oli valmistettu vahvasti kietoutuneeseen vektoritilaan. Vaikka heidän argumenttinsa osoittautuikin myöhemmin kestämättömäksi, niin se toi kuitenkin konkreettisella tavalla esille kvanttimekaniikan yhden oudoimmista piirteistä ja ansaitsee siksi vielä huomion.

EPR analysoivat kyseistä systeemiparia asettamalla kaksi lisäehtoa, joita he kutsuivat todellisuus- ja lokaalisuusehdoiksi, (R) ja (L). Heidän mukaansa nämä ehdot olivat minkä tahansa järkevän fysikaalisen teorian luonnollisia ja välttämättömiä osia. Ehdot ovat:

(R) jos fysikaalisen suureen arvo voidaan määrittää itse systeemiä mitenkään muuttamatta, niin tällä systeemillä on ominaisuus joka vastaa suureen kyseistä arvoa [24];

(L) jos kaksi systeemiä ei vuorovaikuta keskenään, niin toiselle systeemille suoritettu mittaus ei millään tavoin muuta toista systeemiä [25].

Einsteinin, Podolskyn ja Rosenin alkuperäinen esimerkki käytti paikka- ja liikemääräsuureita, joka edellyttää ääretönulotteista teoriaa vaatien tekniikoita joita ei voi tässä yhteydessä käyttää. Vuonna 1951 David Bohm [26] muotoili käsitteellisesti täysin vastaavan, mutta matemaattisesti täsmällisen ja yksinkertaisemman esimerkin käyttäen tilaan $\Psi^-$ preparoitua kubittiparia. Bohmin esimerkkiä käyttäen EPR-argumentti oli seuraava:

Voimme suorittaa minkä tahansa osasysteemisuureen, esimerkiksi suureen $A$ mittauksen ja saamme aina jomman kumman tuloksen $\pm 1$. Koska systeemit $\mathcal{S}_1$ ja $\mathcal{S}_2$ eivät vuorovaikuta keskenään, niin ehdon (L) mukaan osasysteemiin $\mathcal{S}_1$ kohdistettu mittaus ei voi mitenkään muuttaa osasysteemiä $\mathcal{S}_2$. Mutta tilan $\Psi^-$ sisältämän vahvan negatiivisen korrelaation johdosta tiedämme kuitenkin, että jos tämä mittaus tuottaa tuloksen $+1$, niin systeemin $\mathcal{S}_2$ vastinsuureen arvon täytyy olla $-1$, ja jos tulos on $-1$, niin tämä arvon on $+1$. Ehdon (L) nojalla tämä määritys ei mitenkään muuta systeemiä $\mathcal{S}_2$, joten reaalisuusehdon (R) nojalla systeemin $\mathcal{S}_2$ vastinsuureella on jompi kumpi mahdollisista arvoistaan $\pm 1$. Lisäksi tämän arvon on oltava systeemillä $\mathcal{S}_2$ jo valmiina, heti kun systeemipari on valmistettu kyseiseen tilaan, sillä $\mathcal{S}_1$-mittaus ei mitenkään muuta systeemiä $\mathcal{S}_2$. Voimme toistaa tämän argumentin suorittamalla systeemille $\mathcal{S}_1$ suureen $B$ mittaus ja taas päätellä että systeemin $\mathcal{S}_2$ vastinsuureella on jompi kumpi mahdollisista arvoistaan. Selvästikään tila $\Psi^-$ ei sisällä tällaista informaatiota, joten Einstein, Podolsky ja Rosen päättelivät, että kyseisessä esimerkkitapauksessa kvanttimekaniikan tilakuvaus ei sisällä täydellistä tietoa systeemistä $\mathcal{S}_2$. Argumentti on symmetrinen systeemien $\mathcal{S}_1$ ja $\mathcal{S}_2$ suhteen.

Voidaan helposti osoittaa, että jokainen edellä kuvatun kaltaisen vahvan korrelaation sisältämä, ehdot (R) ja (L) täyttävä probabilistinen teoria toteuttaa Bellin epäyhtälöt. Kvanttimekaniikka sisältää vahvan korrelaation mutta rikkoo Bellin epäyhtälöt, joten se ei ole (R,L)-teoria. [27] Reaalisuusehto (R) `riittävänä todellisuusehtona’ on harmiton, vrt. [1/Luku 4]. Jos ehto (R) hyväksytään, niin kvanttimekaniikka on ehdon (L) mielessä epälokaalinen teoria.

Huomautus 4. On tärkeä huomata, että yhdistämissääntöjen vaatimus eri alisysteemisuureiden yhteismitattavuudesta (joka siis toteutuu kvanttimekaniikan yhdistettyjen systeemien teoriassa) ei edellytä ehtoa (L). Eri alisysteemisuureiden yhteismitattavuusvaatimusta kutsutaan usein myös lokaalisuusehdoksi, joten käsillä voi olla sekaannus ellei asiayhteydessä selkeästi kerrota mistä lokaalisuuskäsitteestä kulloinkin on puhe. $\square$

Bellin epäyhtälö -testi on perusrutiini yhdistetyn systeemin, esimerkiksi juuri kubittiparin, tilan kietoutumisen varmistamiseksi. Kiista kvanttimekaniikan ja vahvan korrelaation realistis-lokaalisten teorioiden keskinäisestä pätevyydestä on kuitenkin haastavampi kokeellinen kysymys. Mahdollisten `salaliittoteorioiden’ kumoamiseksi systeemiparin osasysteemeille suoritettavien mittausten on oltava toisistaan täysin riippumattomia, mittausasemien analysaattorien satunnaiset asettamiset (esim. polarisaattoreiden suuntavalinnat) ja tulosten rekisteröinnit on suoritettava niin, että Einsteinin kausaalisuuden rajoissa ei ole mahdollista kommunikoida mittaustapahtumien yksityiskohdista havaintoasemien kesken. Tämä vaatimus pystyttiin toteuttamaan oleellisilta osiltaan ensimmäisen kerran polaarisaatiokietoutuneilla fotonipareilla jo Alain Aspectin ryhmän kokeissa 1982 [28] ja täydellisemmin Anton Zeilingerin ryhmän vastaavassa kokeessa, jossa havaintoasemat olivat noin 40 m etäisyydellä toisistaan, joten periaatteellista mittausaikaa oli käytössä noin 1,3 µs. Yksittäinen mittaus kesti noin 0,1 µs. [29] Toinen lähde mahdollisille `salaliittoteorioille’ on ollut puutteellinen havaintotehokkuus: rekisteröityjen fotoniparien osuus tuotetuista fotonipareista on oltava riittävän suuri, jotta tilastollinen otos olisi luotettava. Tämä mahdollinen `porsaanreikä’ pystyttiin täyttämään vuosituhannen alussa. [30] EPR-kokeissa kvanttimekaniikka on saanut vahvan tuen kun taas vahvan korrelaation (R,L) -teoriat ovat osoittautuneet kokeellisesti epäpäteviksi.

Kuvassa 3 on Aspectin ryhmän historiallisen kokeen kaaviokuva. Siinä polarisaatiokietoutunut fotonipari, aallonpituuksin $\lambda_1=551,3 \, \mathrm{nm}$ ja $\lambda_2=422,7\, \mathrm{nm}$, syntyy kalsiumatomin isotoopin $ {}^{40}{\rm Ca}$ hyperhienorakenteen purkautuessa välitilan kautta perustilaan ($4p^2\,{}^1S_0\to 4s4p\,{}^1P_1\to 4s^2\,{}^1S_0$), välitilan elinaika on noin 5 ns. Kumpaakin vaihtokytkintä $C_I$ ja $C_{II}$ seuraa kaksi erisuuntaista polarisaattoria ja fotodetektorit. Koinsidenssimonitoroinnilla varmistetaan, että rekisteröidyt fotonit ovat peräisin samasta atomista (rekisteröinnit riittävän suppeassa aikaikkunassa). Vaihtokytkimet toimivat noin 10 ns välein kun taas niiden etäisyys $L/c=40\, \mathrm{ns}$. Vaikka mittausasemat olivat Einsteinin kausaalisuuden mielessä riippumattomat, niin kytkinten vaihto ei ollut täysin satunnaista. Kytkimet toimivat toisistaan riippumattomasti mutta kvasiperiodisesti. Käytetyillä suunnilla $(\boldsymbol{a},\boldsymbol{b}),(\boldsymbol{a}’,\boldsymbol{b}),(\boldsymbol{a}’,\boldsymbol{b}’)=22,5^o, (\boldsymbol{a},\boldsymbol{b}’)=67,5^o$ suoritettujen polarisaatiomittausten koinsidenssitodennäköisyyksiä luonnehtiva kvanttimekaaninen tunnusluku $S_{QM}=0,112$, kun taas klassisen teorian mukaan sen arvo on $ S_{\rm klassinen}\leq 0$. [31] Kokeelliseksi arvoksi saatiin $S_{\rm exp}=0,101\pm 0,020$.

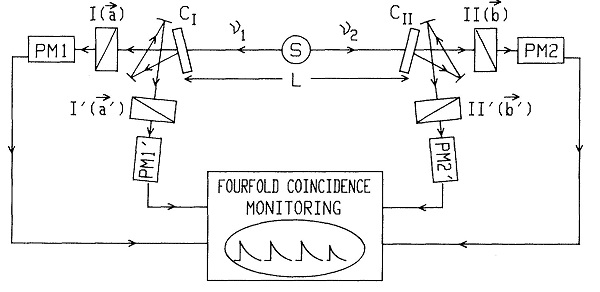
Kuva 3. Kaaviokuva Aspect et al 1982-koejärjestelystä.

5. Kaksi sovellusta

Kvanttikietoutumisella on useita informaatioteoreettisia sovelluksia, joista ehkä erikoisin ja hämmästyttävin on teleportaatio. Kvanttimekaniikka rajoittaa kopiointia, 5.1, mutta avaa uuden vuorovaikutuksettoman tiedonsiirron mahdollisuuden, kvanttiteleportaation, 5.2. Teleportaation avulla voidaan myös vuorovaikutuksettomia objekteja saattaa kietoutuneeseen tilaan. Kvanttikietoutumisella on myös peliteoreettisia sovelluksia, joista luvussa 5.3 on eräs esimerkki.

5.1 Kvanttikopionti

Kopiointi ja monistaminen ovat tuttuja arkirutiineja. Kopiointi on prosessi, jossa alkuperäisestä objektista, esimerkiksi asiakirjasta tai sähköisestä dokumentista tuotetaan identtinen kaksoiskappale. Menemättä kopioinnin tekniseen toteutukseen sen perusajatuksen voi esittää eräänlaisena `mustana laatikkona’, johon tuodaan sekä kopioitava kohde, esim. A4-asiakirja tai sähköinen dokumentti, että tyhjä paperi tai vapaata muistitilaa, ja josta saadaan ulos alkuperäinen ja sen kopio, symbolisesti:

$\;\;\;\;\;\;$$\{({\rm A}4,{\rm teksti}), ({\rm A}4,{\rm blanko})\} \ {\mapsto}\ \{({\rm A}4,{\rm teksti}), ({\rm A}4,{\rm teksti})\}.$

Kvanttikopioinnin perusidea on sama mutta kvanttimekaniikan tila-suure -rakenteen nojalla kvanttikopioinnilla on luonnollista tarkoittaa prosessia, joka monistaa tiettyyn tilaan $\rho$ valmistetun systeemin $\mathcal{S}$. Alkuperäisen, tilaan $\rho$ valmistetun systeemin $\mathcal{S}$ lisäksi on oltava riittävä määrä samankaltaisia [32] systeemejä $\mathcal{S}_i$, $i=1,\ldots, N$, eräänlaisessa alkutilassa, blanko-tilassa $\rho_b$. Kvanttikopioinnin perusvaatimus on näin lausuttavissa symbolisesti muodossa

$\;\;\;\;\;\;$$\{(\mathcal{S},\rho),(\mathcal{S}_1,\rho_b),\ldots, (\mathcal{S}_N,\rho_b)\} \mapsto \{(\mathcal{S},\rho),(\mathcal{S}_1,\rho),\ldots,(\mathcal{S}_N,\rho)\}$

jonka luonnollinen matemaattinen mallinnus on annettavissa $1+N$ systeemin tilamuunnoksena [1/Luku 7], kopiokuvauksena

(5.1)$\;\;\;$$\hat k:\rho\otimes\rho_b\otimes\cdots\otimes\rho_b\mapsto \rho\otimes\rho\otimes\cdots\otimes\rho,$

joka sisältää sen ajatuksen, että kopioitava systeemi $\mathcal{S}$ sekä systeemit $\mathcal{S}_i$ joihin kopioidaan ovat toisistaan (sekä dynaamisesti että tilastollisesti) riippumattomia paitsi ennen niin myös jälkeen kopioinnin. Kopionnilta on luonnollista vaatia universaalisuus: kopiointi voidaan toteuttaa systeemin $\mathcal{S}$ mille tahansa tilalle $\rho\in\boldsymbol{S}(\mathcal{H})$. Lisäksi on luonnollista vaatia, että kopiointi säilyttää tilajoukon $\boldsymbol{S}(\mathcal{H})$ keskeiset rakenteet, kuten esimerkiksi tilan $\rho$ mahdollisen seosrakenteen, tai puhtaan tilan $\rho$ superpositiorakenteen.

Tarkastellaan tapausta $N=1$, jolloin $\hat k(\rho\otimes\rho_b)=\rho\otimes\rho$ kaikilla $\rho\in\boldsymbol{S}(\mathcal{H})$. Jos nyt $\rho=\lambda\rho_1+(1-\lambda)\rho_2$, joillekin $0\ne\lambda\ne 1$, $\rho_1\ne\rho_2$, niin

$\;\;\;\;\;\;$$\hat k(\rho\otimes\rho_b)=\rho\otimes\rho=\lambda^2\rho_1\otimes\rho_1+\lambda(1-\lambda)(\rho_1\otimes\rho_2+\rho_2\otimes\rho_1)+(1-\lambda)^2\rho_2\otimes\rho_2.$

Toisaalta kopioinnin tulisi säilyttää myös tilan seosrakenne, joten kuvauksen pitäsi toteuttaa myös ehto

$\;\;\;\;\;\;$$\hat k(\rho\otimes\rho_b)=\hat k\bigg(\lambda\rho_1\otimes\rho_b+(1-\lambda)\rho_2\otimes\rho_b\bigg)=\lambda\hat k(\rho_1\otimes\rho_b)+(1-\lambda)\hat k(\rho_2\otimes\rho_b)=\lambda\rho_1\otimes\rho_1+(1-\lambda)\rho_2\otimes\rho_2.$

On selvää, että yhtälöiden oikeat puolet eivät voi olla samoja kaikilla tiloilla $\rho$; vastaava argumentti voidaan antaa puhtaiden tilojen superpositioiden avulla. Toisin sanoen, tällaista kuvausta ei voi olla olemassa.

Kuva 4. Toimiva Victoriaaninen kopiokone vuodelta 1913 $\ldots$

Universaali kopiokone ei ole kvanttimekaniikan mukaan mahdollinen. Tätä mahdottomuustulosta voidaan kiertää kahdella eri tavalla. Voimme luopua universaalisuusvaatimuksesta, eli voimme kysyä onko olemassa kopiokuvaus $\hat k$, joka kopioi tarkasti tietyt ennalta valitut tilat. Toinen mahdollisuus on, että tingitään kopioinnin tarkkuudesta, eli tyydytään siihen, että kopio $\hat k(\rho\otimes\rho_b)$ on jossakin sopivassa mielessä lähellä ideaalia $\rho\otimes\rho$, siis että todennaköisyydet $p^{\mathsf{E}\otimes\mathsf{E}}_{\hat k(\rho\otimes\rho_b)}$ ovat lähellä todennäköisyyksiä $p^\mathsf{E}_\rho\times ^\mathsf{E}_\rho$ kaikilla (tai ainakin joillekin) suureille $\mathsf{E}\in\boldsymbol{O}(\mathcal{H})$. Kumpaakin mahdollisuutta on tutkittu ja niissä on saavutettu mielenkiintoisia, käytännön sovellustenkin kannalta hyödyllisiä tuloksia.

Emme tässä yhteydessä paneudu näihin mahdollisuuksiin, vaan tarkastelemme erästä toista kopiointiin läheisesti liittyvää toimintoa, eräänlaista telekopiointia, jolle avautuu kvanttifysiikassa aivan uusi ja täysin yllättävä mahdollisuus. Todettakoon kuitenkin, että kopioinnin mahdottomuus voidaan kääntää myös voimavaraksi, sillä kopiointiyritys jättää välttämättä jälkensä.

5.2 Kvanttiteleportaatio

Kvanttiobjektin tilaa ei voida kopioida mutta se voidaan siirtää ilman vuorovaikutusta toiselle, mahdollisesti kaukana olevalle objektille. Prosessi tunnetaan kvanttiteleportaationa. Sen idean esittiät Charles Bennet et al jo vuonna 1993 [33] ja sen ensimmäisistä kokeellisista toteutuksista raportoivat Dik Bouwmeester et al [34] 1997 sekä D. Boschi et al [35] 1998.

Teleportaatioon tarvitaan kolme kvanttiobjektia ja kaksi mittausasemaa, lähetysasema, josta tila teleportoidaan, ja vastaanottoasema, jossa tila vastaanotetaan. Koska kummallakin asemalla suoritetaan tiettyjä operaatioita niin on käytännöllistä nimetä nämä operaattorit, kvanttikirjallisuutta seuraten lähettäjänä Alice, vastaanottajana Bob. Tarkastelemme tätä prosessia kubittiesimerkin avulla.

Kubittipari $\mathcal{S}_{23}=(\mathcal{S}_2,\mathcal{S}_3)$ valmistetaan aluksi vahvasti kietoutuneeseen tilaan, esimerkiksi Bellin vektoritilaan $\Psi_{23}^-$,

$\;\;\;\;\;\;$$\Psi_{23}^- =\frac 1{\sqrt 2}(|{+}\rangle_2|{-}\rangle_3-|{-}\rangle_2|{+}\rangle_3)=\frac 1{\sqrt 2}(|{+ -}\rangle-|{- +}\rangle).$ [36]

Kubitti $\mathcal{S}_2$ lähetetään lähetysasemalle ja kubitti $\mathcal{S}_3$ vastaanottoasemalle niin, että tila $\Psi^-_{23}$ säilyy. [37] Alicelle ohjataan lisäksi kubitti $\mathcal{S}_1$, jonka tila halutaan siirtää Bobin hallussa olevalle kubitille $\mathcal{S}_3$.

Olkoon $S_1$ alunperin jossakin vektoritilassa

(5.2)$\;\;\;$$\phi_1 = a|{+}\rangle_1+b|{-}\rangle_1= a|{+}\rangle+b|{-}\rangle,\ \ \ |a|^2+|b|^2=1.$

Koska $\mathcal{S}_1$ on aluksi riippumaton parista $\mathcal{S}_{23}$, niin kolmikon $(S_1,S_{23})$ tila on tulotila $\phi_1\otimes\Psi_{23}^- $. Tensoritulon lineaarisuuden nojalla tämä tila voidaan kirjoittaa superpositiona [38]

(5.3)$\;\;\;$$\phi_1\otimes \Psi_{23}^-=(a|{+}\rangle_1+b|{-}\rangle_1) \otimes \frac{1}{\sqrt 2}(|{+}\rangle_2|{-}\rangle_3-|{-}\rangle_2|{+}\rangle_3)$

$\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;$$=\frac{a}{\sqrt 2}(|{+ + -}\rangle \;- |{+\; – +}\rangle) + \frac{b}{\sqrt 2}(|{- + -}\rangle \;- |{-\; – +}\rangle)$.

Kubitin $\mathcal{S}_1$:n tilan siirtäminen kubitille $\mathcal{S}_3$ toteutetaan suorittamalla parille $(S_1,S_2)$ sopiva 4-arvoisen suureen mittaus, ns. Bellin tila mittaus, BSM. Tällä tarkoitetaan Bellin kantavektoreiden (3.3)-(3.4) määrittelemän (tarkan) suureen

$B_{12} =b_1|{\Phi^+_{12}}\rangle\langle{\Phi^+_{12}}|+b_2|{\Phi^-_{12}}\rangle\langle{\Phi^-_{12}}|+b_3|{\Psi^+_{12}}\rangle\langle{\Psi^+_{12}}|+b_1|{\Psi^-_{12}}\rangle\langle{\Psi^-_{12}}|$

mittausta. Tässä $b_1,b_2,b_3,b_4$, $b_i\in\mathbb{R}$, $b_i\ne b_j$, $i\ne j$, ovat suureen $B_{12}$ mahdolliset mittaustulokset; niillä on tässä vain kirjanpidollinen merkitys.

Koska vektorit $\Phi^\pm_{12},\Psi^\pm_{12}$ muodostavat avaruuden $\mathcal{H}_1\otimes\mathcal{H}_2$ kannan, ja esimerkiksi

$|{+ + -}\rangle=|{+ +}\rangle_{12}|{-}\rangle_3= \frac 1{\sqrt 2}(\Phi^+_{12}+\Phi^-_{12})\otimes|{-}\rangle_3,$

niin $\phi_1\otimes\Psi_{12}^-$ voidaan lausua myös superpositiona

$\;\;\;\;\;\;$$\phi_1\otimes\Psi_{23}^-=\frac{a}{\sqrt 2}(|{+ +}\rangle|{-}\rangle – |{+ -}\rangle|{+}\rangle) + \frac{b}{\sqrt 2}(|{- +}\rangle|{-}\rangle – |{- -}\rangle|{+}\rangle)\\\;\;\;\;\;\;\;\;\;\;\;\;\;\;= \frac 12\Phi^+_{12}\otimes(a|{-}\rangle -b|{+}\rangle)+\frac 12\Phi^-_{12}\otimes(a|{-}\rangle +b|{+}\rangle)\\{}\quad \;\;\;\;\;\;\;\;\;\;\;\;\;\; +\frac 12\Psi^+_{12}\otimes(-a|{+}\rangle +b|{-}\rangle)+\frac 12\Psi^-_{12}\otimes(-a|{+}\rangle -b|{-}\rangle)$

(5.4)$\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;$$= \frac 12\Phi^+_{12}\otimes (U_y\phi)+ \frac 12\Phi^-_{12}\otimes(U_x\phi)+\frac 12\Psi^+_{12}\otimes (U_z\phi)+ \frac 12\Psi^-_{12}\otimes (-\phi)$,

missä vektoritilat $\phi=a|{+}\rangle + b|{-}\rangle$, $U_z\phi, U_y\phi, U_x\phi$ liittyvät nyt systeemin $\mathcal{S}_3$, vrt. tila (5.3). Tässä

$\;\;\;\;\;\;$$U_z=\left(\begin{matrix}-1&0\\0&1\end{matrix}\right)\ {,}\ U_y=\left(\begin{matrix}0&-1\\ 1&0\end{matrix}\right)\ {,}\ U_x=\left(\begin{matrix}0&1\\1&0\end{matrix}\right)$.

Nämä matriisit kuvaavat $\pi$:n kiertoja vastaavien koordinaattiakselien ympäri, ja ne voidaan helposti implementoida esim. fotonien tapauksessa ns. aaltolevyillä [39].

Hajotelman (5.4) merkitys on kahdenlainen. Ensinnäkin suureen $B_{12}$ mittaustulostodennäköisyydet saadaan nyt suoraan kehitelmän kertoimien itseisarvon neliöinä; esimerkiksi

$\;\;\;\;\;\;$$p^{B_{12}}_{\rho_{12}}(\{b_1\})=\left\langle{\phi_1\otimes\Psi^-_{23}}|{P[\Phi_{12}^+]\otimes I_3\, \phi_1\otimes\Psi_{23}^-}\right\rangle=\frac 14\left\langle{U_y\phi}|{U_y\phi}\right\rangle=\frac 14.$

Toinen tärkeä seikka liittyy (vektori)tilan $\phi_1\otimes\Psi_{23}^-$ muuntumiseen suureen $B_{12}$ mittauksessa. Jos tämä mittaus on ns. Lüdersin mittaus [1/Luku 7], niin tämä tila muuntuu projektiivisesti, jolloin esimerkiksi

$\;\;\;\;\;\;$$P[\phi_1\otimes\Psi_{23}^-]\mapsto \frac 14\, P[\Phi_{12}^+]\otimes P[U_y\phi]$

on ehdollinen tilamuunnos, ehdolla, että $B_{12}$-mittaus tuottaa tuloksen $b_1$, joka ehto toteutuu tässä todennäköisyydellä $\frac 14$. Nämä kaikki neljä ehdollista tilaa ovat objektin $\mathcal{S}_3$ kannalta separoituvia kun taas objektit $\mathcal{S}_1$ ja $\mathcal{S}_2$ ovat toisiinsa vahvasti kietoutuneita.

Suureen $B_{12}$ mittaus lähetysasemalla tuottaa varmuudella jonkin tuloksista $b_1,b_2,b_3,b_4$ ja minkä tahansa niistä todennäköisyydellä $\frac 14$. Alice, mittauksen suorittajana, rekisteröi kyseisen tuloksen. Olkoon se esimerkiksi $b_3$. Alice välittää tuloksen Bobille klassista kommunikointia, esimerkiksi puhelinta käyttäen. Saatuaan tiedon tuloksesta Bob suorittaa objektille $\mathcal{S}_3$ tarvittavan operaation, tuloksen $b_3$ tapauksessa $-\pi$:n kierron $z$-akselin ympäri:

$\;\;\;\;\;\;$$P[U_z\phi]\mapsto U_z^*P[U_z\phi]U_z=P[U_z^*U_z\phi]=P[\phi].$

Objektin $\mathcal{S}_3$ tilaksi on näin saatu objektin $\mathcal{S}_1$ alkuperäinen tila. Samalla objektin $\mathcal{S}_1$ tila on muuntunut täysin polaroituneeksi tilaksi $\frac 12\, I$, joten tila ei kopioitunut.

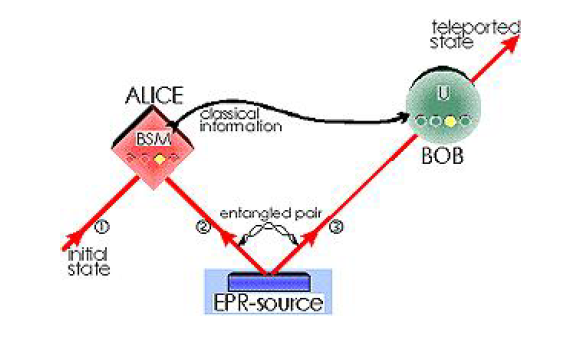
Kuva 5. $\;\;$$\ldots$ ja 84 vuotta myöhemmin: onnistuneen kvanttiteleportaation havainnekuva tekijöiden Bouwmeester et al (1997) mukaan: Alice siirtää kubitin $1$ tilan Bobin hallussa olevalle kubitille $3$ suorittamalla kubittiparille $(1,2)$ Bellin tila mittauksen $BSM$.

Huomautus 5. Kietoutuneita pareja syntyy tyypillisesti erilaisten vuorovaikutusten seurauksena. Huomautuksessa 3 jo todettiin, että kaksi systeemiä voidaan saattaa kietoutuneeseen tilaan ilman vuorovaikutusta. Tämä voidaan toteuttaa ns. kietoutumisvaihtona, jonka idea on tiivistetysti seuraava. Valmistetaan riippumattomasti kaksi vahvasti kietoutunutta kubittiparia $\mathcal{S}_{12}$ ja $\mathcal{S}_{34}$. Suoritetaan Bellin tila mittaus parille $\mathcal{S}_{23}$. Mittauksen seurauksena objektit $\mathcal{S}_1$ ja $\mathcal{S}_4$ ajautuvat vahvasti kietoutuneeseen tilaan. Objektit $\mathcal{S}_1$ ja $\mathcal{S}_4$ eivät ole vuorovaikuttaneet keskenään, ne voivat olla kaukana toisistaan ja toisilleen tuntemattomissa paikoissa. Todettakoon vielä, että teleportaatiota ei tiedetä tapahtuvan luonnossa ilman ihmisen vaikutusta. $\square$

5.3 Eräs peli

Kvanttikietoutumisella on myös peliteoreettisia sovelluksia. Erityisesti sen avulla voidaan voittaa pelejä joita ei voi voittaa klassisella strategialla. Seuraava esimerkki on mukaeltu L. Vaidmanin artikkelista ”Variations on the Theme of the Greenberger-Horne-Zeilinger Proof”. [40]

Peli ja sen säännöt. Peli on kysymys-vastaus-peli ja siihen osallistutaan kolmen pelaajan joukkueilla. Pelaajat saavat suunnitella ja valmistella pelistrategiansa haluamallaan tavalla ennen kuin heidät viedään kolmeen eri paikkaan $A$, $B$, ja $C$. Kullekin joukkueen jäsenelle tullaan esittämään sopivana hetkenä yksi kahdesta mahdollisesta kysymyksestä, $X$ tai $Y$. Kumpaankin kysymykseen on kaksi mahdollista vastausta, kyllä (1) tai ei (-1). Pelin sääntöihin kuuluu, että

joko kultakin pelaajalta kysytään $X$,
tai yhdeltä pelaajalta kysytään $X$ ja kahdelta muulta $Y$.

Joukkue voittaa pelin, jos vastausten tulo on

$-1$, jos kaikilta kysyttiin $X$,
$+1$, jos yhdeltä kysyttiin $X$ ja kahdelta muulta $Y$.

Kunkin pelaajan on annettava vastauksensa niin nopeasti, ettei pelaajien välillä voi tapahtua kommunikointia. Voiko joukkue valita sellaisen pelistrategian, joka tuo varmuudella voiton?

Klassinen strategia. Joukkueen $\boldsymbol{K}$ vanhat herrat Salviati, Sagredo ja Simplicio ovat kokeneita pohdiskelijoita ja keskustelukumppaneita [41] ja he ovat päättäneet kokeilla pelionneaan. He alkavat pohtia pelistrategiaansa palauttaen aluksi mieliin, että puhdas arpominen ei tuo toivottavaa tulosta. Ensinnäkin mahdollisia ennakkoon yhtä todennäköisiä kysymyssarjoja on neljä: $\ (X_A,X_B,X_C)$, $(X_A,Y_B,Y_C)$, $(Y_A,X_B,Y_C)$, ja $(Y_A,Y_B,X_C)$. (Tässä esim. $X_A$ tarkoitaa, että paikassa $A$ olevalta pelaajalta kysytään $X$). Kunkin yksittäisen vastaussarjan todennäköisyys on $(\frac 12)^3=\frac 18$. Jos kaikilta kysytään $X$, niin suotuisia vastauskolmikkoja on neljä kahdeksasta, joten tuloksen $-1$ todennäköisyys on $\frac 14\cdot \frac 12=\frac 18$, ja jos taas yhdeltä kysytään $X$ ja kahdelta muulta $Y$, niin kussakin tapauksessa suotuisia vastauksia on neljä kahdeksasta, joten kokonaistuloksen $+1$ todennäköisyys on $\frac 34\cdot\frac 12=\frac 38$. Pelin onnistumistodennäköisyys arpomalla on siis $\frac 18+\frac 38=\frac 12$, joka ei tuo varmaa voittoa.

Kuva 6. Salviati, Sagredo ja Simplicio strategiapalaverissa.

Salviati, Sagredo, ja Simplicio hylkäävät arpomisen ja alkavat pohtia muita pelistrategioita. Pohdinta kulkee seuraavia uria. Kukin pelaaja joutuu antamaan kumpaan tahansa hänelle esitettävään kysymykseen joko vastauksen $+1$ tai $-1$; voimme päättää mahdolliset vastauksemme ennakkoon tässä yhdessä tai siirtää vastausten antamisen siihen hetkeen, jolloin kysymys esitetään. Mutta tällöin olemme eri paikoissa eikä kommunikoinnin mahdollisuutta ole. Päätöksenteon siirtämisestä kysymyshetkeen ei siksi voi olla mitään hyötyä; joudumme vain turvautumaan arpomiseen joka ei nyt auta. Vastaukset on siis parasta sopia etukäteen. Katsokaamme miten matemaattinen päättely voi meitä tässä auttaa. Ratkaistavana on siis yhtälöt

\begin{eqnarray*}X_AX_BX_C&=&-1\\X_AY_BY_C&=&1\\Y_AX_BY_C&=&1\\Y_AY_BX_C&=&1.\end{eqnarray*}

Mutta tämä on mahdotonta sillä yhtälöiden vasempien puolten tulo on $X_A^2Y_A^2X_B^2Y_B^2X_C^2Y_C^2=1$ kun taas oikeat puolet antavat tuloksi -1.

Salviati, Sagredo ja Simplicio vetäytyvät pelistä todeten, ettei varman voiton strategiaa voi olla.

Kvanttistrategia. Alice ja Bob ovat myös kuulleet pelistä ja he päättävät muodostaa mentorinsa Charlien kanssa joukkueen $\boldsymbol{Q}$. He ovat tottuneet käyttämään modernia teknologiaa ja heille on tuttua paitsi aito sattuma niin myös se, että päätöksenteon lykkäämisestä saattaa koitua lisäetua. Pelaajat ymmärtävät heti, että sen paremmin puhdas arpominen kuin vastausten etukäteinen kiinnittäminenkään ei tuota toivottua tulosta. Hetken mietittyään he päätyvät valmistamaan kolmen kubitin $\mathcal{S}_A$, $\mathcal{S}_B$, ja $\mathcal{S}_C$ yhdisteen Greenbergerin-Hornen-Zeilingerin tilaan

$$\label{GHZtila}|{\rm GHZ}\rangle=\frac 1{\sqrt 2}(|{+++}\rangle-|{-\; – -}\rangle.$$

He sopivat, että paikkaan $A$ menevä pelaaja ottaa mukaansa objektin $\mathcal{S}_A$, paikkaan $B$ menevä objektin $\mathcal{S}_B$, ja $C$:hen menevä $\mathcal{S}_C$:n, niin, että kokonaistila $|GHZ\rangle$ säilyy muuttumattomana.

Kuva 7. Alice, Bob ja Charlie varman pelistrategian lumoissa.

Varsinaiseksi pelistrategiaksi he sopivat, että jos pelaajalta kysytään $X$, hän suorittaa objektilleen suureen $\sigma_1$ mittauksen ja jos häneltä kysytään $Y$, hän suorittaa $\sigma_2$-mittauksen antaen mittaustuloksensa, joko +1 tai -1, vastauksenaan. Kyseisessä tapauksessa kunkin pelaajan yksittäinen mittaus, $\sigma_1$ tai $\sigma_2$ tuottaa kumman tahansa tuloksen $\pm 1$ samalla todennäköisyydellä $\frac 12$. Mutta tilassa $|GHZ\rangle$ näiden suureiden mittaustulokset ovat toisiinsa kietoutuneita niin, että jos jokaiselta kysytään $X$, mittaukset $\sigma^A_1$, $\sigma^B_1$, ja $\sigma^C_1$ tuottavat välttämättä sellaiset tulokset $i^A, i^B, i^C\in\{-1,+1\}$, että $i^Ai^B i^C=-1$. Vastaavasti, jos yhdeltä kysytään $X$ ja kahdelta muulta $Y$, mittaustulokset toteuttavat välttämättä ehdon $i^Ai^B i^C=1$. Alice, Bob ja Charles ottavat mielihyvin uhkapelitarjouksen vastaan.

6. Identtiset systeemit

Jos kaksi objektia ovat identtiset, toisistaan erottumattomat, niin niiden identifiointi yhdisteen $(\mathcal{S},\mathcal{S})$ osina ei voi paljastaa kumpi kumpikin on. Tämä tarkoittaa sitä, että vain sellaiset $\rho\in\boldsymbol{S}(\mathcal{H}\otimes\mathcal{H})$ ovat yhdisteen mahdollisia tiloja, joille kaikkien osasysteemisuureiden mittaustulostodennäköisyydet (2.3) ja (2.4) ovat samat aina kun alisysteemisuureet $\mathsf{E}$ ja $\mathsf{F}$ ovat samat:

$\;\;\;\;\;\;$$\mathrm{tr}[{\rho\, \mathsf{E}(X)\otimes I}]= \mathrm{tr}[{\rho\, I\otimes\mathsf{E}(X)}],$

kaikilla suureilla $\mathsf{E}$ ja testijoukoilla $X$. Erityisesti, jos $\rho$ on puhdas ja hajoava, siis annettavissa vektorina $\varphi\otimes\psi, \left\| \varphi \right\|=\left\| \psi \right\|=1$, niin tämä tarkoittaa sitä, että kaikilla $E\in\boldsymbol{E}(\mathcal{H})$.

$\;\;\;\;\;\;$$\left\langle{\varphi}|{E\varphi}\right\rangle=\left\langle{\varphi\otimes\psi}|{E\otimes I\,\varphi\otimes\psi}\right\rangle=\left\langle{\varphi\otimes\psi}|{I\otimes E\,\varphi\otimes\psi}\right\rangle=\left\langle{\psi}|{E\psi}\right\rangle,$

Tämä ehto toteutuu vain jos $\psi=z\varphi, z\in\mathbb{C}, |z|=1$. Sen sijaan muotoa $\varphi\otimes\psi\pm\psi\otimes\varphi$ olevat vektorit eivät erota alisysteemejä, joten ne edustavat (normitettuina) parin $(\mathcal{S},\mathcal{S})$ mahdollisia puhtaita tiloja. Vektori $\varphi\otimes\psi+\psi\otimes\varphi$, samoin kuin $\varphi\otimes\varphi$, on symmetrinen, kun taas $\varphi\otimes\psi-\psi\otimes\varphi$ on antisymmetrinen parinvaihdon suhteen. [42]

Kuten muotoa $\varphi\otimes\psi$ olevien vektoreiden lineaarikombinaatiot määrittelevät (äärellisulotteisessa tapauksessa) koko Hilbertin avaruuden $\mathcal{H}\otimes\mathcal{H}$, niin samalla tavalla symmetristen (vast. antisymmetristen) vektoreiden $\varphi\otimes\psi+\psi\otimes\varphi$ ( vast. $\varphi\otimes\psi-\psi\otimes\varphi$) lineaarikombinaatiot määrittelevät avaruuden $\mathcal{H}\otimes\mathcal{H}$ symmetrisen (vast. antisymmetrisen) aliavaruuden $\mathcal{H}\otimes_s\mathcal{H}$ (vast. $\mathcal{H}\otimes_a\mathcal{H}$). [43] Molemmat ovat itsessään Hilbertin avaruuksia ja niillä on vain nollavektori yhteisenä vektorina.

Kubittiesimerkissä olemme käyttäneet Bellin kantavektoreita. Niistä kolme, $\Phi^+,\Phi^-,\Psi^+$, on symmetrisiä, ja yksi, $\Psi^-$, antisymmetrinen. Niinpä avaruuden $\mathbb{C}^2\otimes\mathbb{C}^2$ symmetrinen aliavaruus on kolmiulotteinen ja antisymmetrinen aliavaruus yksiulotteinen.

Kahden identtisen objektin yhdisteen kuvaus perustetaan joko symmetriselle tai antisymmetriselle Hilbertin avaruudelle yleisten periaatteiden mukaisesti. Voidaan osoittaa, että valinta näiden kahden mahdollisuuden kesken riippuu objektin spinominaisuudesta. Spin-statistiikka -lauseena tunnettu tulos sanoo, että jos spin on puolilukuinen (fermioni) niin avaruus on antisymmetrinen $\mathcal{H}\otimes_a\mathcal{H}$ ja jos spin on kokonaislukuinen (bosoni), niin avaruus on symmetrinen $\mathcal{H}\otimes_s\mathcal{H}$.

Fotonit ovat bosoneja, joten fotoneista koostuvan kubittiparin kvanttimekaniikka tulisi näin perustaa kolmiulotteiselle symmetriselle avaruudelle $\mathbb{C}^2\otimes_s\mathbb{C}^2$ kun taas esim. elektroniparin tapauksessa käsillä olisi vektorin $\Psi^-$ generoima yksiulotteinen avaruus. Koska fysikaalisilla objekteilla, kuten kubiteilla on kuitenkin ns. sisäisten vapausasteiden, kuten spin tai polarisaatio, lisäksi myös avaruudellisia, paikkaan ja liikemäärään liittyviä vapausasteita ja identtisten systeemien erottumattomuusvaatimus koskee yhdisteen kokonaistilaa, siis koko avaruuksia $\mathcal{H}\otimes_s\mathcal{H}$ ja $\mathcal{H}\otimes_a\mathcal{H}$, niin tässä kirjoituksessa on voitu jättää huomioimatta kubittien mahdollisesta identtisyydestä aiheutuvat tekijät.

7. Lopuksi

Kvanttimekaniikka sisältää useita klassisesta fysiikasta poikkeavia arkikokemuksen vastaisia piirteitä teorian aidosta todennäköisyysluonteesta kvanttikietoutumiseen. Vaikka ajatus siitä, että jokin näistä piirteistä olisi muita olennaisempi, on heikosti perusteltavissa, ainakin teorian loogisen rakenteen näkökulmasta, niin kvanttikietoutuminen seurauksineen on, varsinkin aiemmin, usein nostettu esille tällaisena ominaisuutena. Näin teki mm. jo Erwin Schrödinger edellä luvussa 3 viitatussa artikkelissaan kirjoittaessaan: ”I would not call [the entanglement] one but rather the characteristic trait of quantum mechanics, the one that enforces its entire departure from classical lines of thought”.

Kvanttimekaniikan `oudot’ piirteet saavat usein lähtökohtaisesti negatiivisen luonnehdinnan kun niitä peilataan klassiseen teoriaan ja arkikokemukseen. On kuitenkin tärkeä huomata, että nämä kaikki piirteet on pystytty valjastamaan uusiksi voimavaroiksi kvanttimekaniikalle pohjautuvien fysiikan teorioiden käytännön sovellusten laajassa kirjossa.

Jää nähtäväksi minkälaisiin sovelluksiin tilojen superposition ja kvanttikietoutumisen mahdollistamat yksittäisobjektien ja objektiparien uudet manipuloinnit, kuten teleportaatio, tulevat johtamaan kvanttiteknologian läpimurtoa odottavalla vuosikymmenellä.

*****

Kiitos kolleegoilleni dosentti Teiko Heinosaarelle, dosentti Jukka Kiukakselle, dosentti Juha-Pekka Pellonpäälle ja professori emeritus Kari Yliselle artikkelin käsikirjoitukseen saamastani palautteesta sekä dosentti Tom Kuuselalle hänen tutkimuslaitteistoonsa liittyvistä keskusteluista ja kuvista 1 ja 2. Kiitos myös FM Riitta Salmenojalle sujuvasta taittotyöstä.

*****

[1] https://www.dimensiolehti.fi kvanttimekaniikan-peruskysymyksia-yhteismittauksista-ja-epatarkkuuksista/

[2] https://www.nature.com/articles/s41586-021-03282-z

[3] Ks. esim. https://www.nature.com/articles/s41586-019-1666-5, tai $\\$ https://www.zhinst.com/others/en/quantum-computing-systems/qccs?msclkid=50bd9e547c8c154fe153fe6e119f4638,$\\$ tai https://www.research.ibm.com/hybrid-cloud/vision/

[4] Jokainen efekti vastaa jonkin kyllä-ei -kokeen kyllä-tulosta.

[5] Käytämme taas perusviitteenä teosta Quantum Measurement, P. Busch, P. Lahti, J.-P. Pellonpää, K. Ylinen, Springer, 2016, jossa tässä kirjoituksessa esitettävät asiat on tarkemmin dokumentoitu.

[6] Kirjoitamme tässä ja myös jatkossa $\mathcal{H}_{12}=\mathcal{H}_1\otimes\mathcal{H}_2$ vaikka yhtäsuuruus tässä tarkoittaa vain sitä, että yhtälön vasen ja oikea puoli ovat rakenneyhtäläiset, isometrisesti isomorfiset, eli `oleellisesti samanlaiset’ vaikkei välttämättä samat. Sama pätee esim. identifiointiin $\mathbf{S}(\mathcal{H}_{12})=\mathbf{S}(\mathcal{H}_1\otimes\mathcal{H}_2)$.

[7] Yhtälöistä 2.1 ja 2.2 voi helposti vakuuttua, ettei kysymys vektorin $\phi\in\mathbb{C}^4$ mahdollisesta hajoavuudesta ole täysin suoraviivainen.

[8] Matriisin $A$ positiivisuus tarkoittaa sitä, että kaikilla vektoreilla $\phi\in\mathbb{C}^4$, luvut $\left\langle{\phi}|{A\phi}\right\rangle\geq 0$. Itse asiassa, riittää, että näin on kaikille hajoaville vektoreille $\phi=\varphi\otimes\psi$.

[9] Jos jompi kumpi suureista $\mathsf{E}$ tai $\mathsf{F}$ on tarkka (projektio-arvoinen) suure, niin suureilla $X\mapsto h_1(\mathsf{E}(X))$ ja $Y\mapsto h_2(\mathsf{F}(Y))$ ei ole muita yhdistettyjä suureita. Tarkkojen spinsuureiden $h_1(A)=(\hat{\boldsymbol{a}}\cdot\mathbf\sigma)\otimes I=P_{\hat{\boldsymbol{a}}}\otimes I-P_{-\hat{\boldsymbol{a}}}\otimes I$ ja $h_2(B)=I\otimes (\hat{\boldsymbol{b}}\cdot\mathbf\sigma)=I\otimes P_{\hat{\boldsymbol{b}}}-I\otimes P_{-\hat{\boldsymbol{b}}}$ (yksikäsitteinen) kaksoissuure $(i,j)\mapsto P_{i\hat{\boldsymbol{a}}}\otimes P_{j\hat{\boldsymbol{b}}}$, $i,j=\pm$, on Esimerkin 2 hajotelma.

[10] Yksiulotteisilla projektioilla on kaksoisrooli, ne edustavat sekä efektejä että puhtaita tiloja.

[11] Ji-Gang Ren et al, ”Ground-to-satellite quantum teleportation”, Nature $\boldsymbol{549}$ (2017) 70-73.

[12] A. Einstein, B. Podolsky, N. Rosen, ”Can Quantum-Mechanical Description of Physical Reality Be Considered Complete?”, Physical Review $\boldsymbol{47}$ (1935) 777-780. Alku voitaisiin sijoittaa myös von Neumannin kirjan Mathematische Grundlagen der Quantenmechanik (1932) lukuun V.1, jossa tarkastellaan mittauksen aiheuttamaa systeemin tilan muuntumista, vrt [1/Luku 7]. Kvanttikietoutuminen on oleellinen osa kvanttimekaanista mittaustapahtumaa.

[13] E. Schrödinger, ”Discussion of probability relations between separated systems”, Proceedings of the Cambridge Philosophical Society $\boldsymbol{31}$ (1935) [käytössä termi `entanglement’], ”Die gegenwärtige Situation in der Quantenmechanik”, Die Naturwissenschaften $\boldsymbol{23}$ (1935), 807-812; 823-828; 844-849 [käytössä termi `Verschränkung’].

[14] N. Bohr, ”Can Quantum-Mechanical Description of Physical Reality Be Considered Complete?”, Physical Review $\boldsymbol{48}$ (1935) 696-702.

[15] J. Bell, ”On the Einstein Podolsky Rosen paradox”, Physics, $\boldsymbol{1}$ (1964) 195-200.

[16] Ääretönulotteisessa tapauksessa tarvitaan matemaattista hienosäätöä, joka tässä sivuutetaan.

[17] Olkoon $\gamma$ kahden kaksiarvoisen todennnäköisyysmitan $\mu_1$ ja $\mu_2$ kytkentä, yhdistetty todennäköisyys, arvopareina $i,j=\pm 1$. Luku ${\rm corr}(\mu_1,\mu_2|\gamma)=\frac{\gamma[11]-\mu_1[1]\mu_2[1]}{\Delta(\mu_1)\Delta(\mu_2)}$ on $\mu_1$:n ja $\mu_2$:n normitettu korrelaatio kytkennän $\gamma$ suhteen. Tässä $\gamma[11]=\sum_{ij}ij\gamma(i,j)$, $\mu_1[1]=\sum_i i\mu_1(i)$, $\mu_2[1]=\sum_jj\mu_2(j)$, ja $\Delta(\mu_1), \Delta(\mu_2)$ mittojen $\mu_1$ ja $\mu_2$ hajonnat (luonnollisesti ehdoilla $\Delta(\mu_1)\ne 0\ne \Delta(\mu_2)$).

[18] Äärettömässä tapauksessa tarvitaan taas matemaattista hienosäätöä.

[19] Jokainen reaaliluku $r$, jolle $0\leq r\leq p=\mu(\{+\})$, $0\leq r\leq \nu(\{+\})$, ja $p+q-r\leq 1$, määrittelee todennäköisyysmittojen $\mu$ ja $\nu$ erään yhdistetyn mitan, kytkennän, ks. [1/ Esimerkki 2, Taustatietoa 5].

[20] Epätriviaali tapaus edellyttää vähintään kolmea suuretta, esimerkiksi $A$ ja $B,B’$. Tarkastelemme tässä neljää suuretta koska tämä on tyypillisin tilanne EPR-kokeissa.

[21] Tällainen mitta olisi esimerkiksi joukon $\{1,\bar 1,1′,\bar 1′,2,\bar 2,2′,\bar 2’\}$ alijoukoille määritelty todennäköisyysmitta $\mu$, jolle esimerkiksi $\mu(\{1,2’\}) =p(a,b’)$. Koska samaan alisysteemiin liittyvät suureet eivät kommutoi keskenään, niin on selvää, että tällaista esitystä ei voida saada kaikissa yhdisteen tiloissa $\rho$.

[22] Ks. esim. Itamar Pitowsky, Quantum Probability – Quantum Logic, Springer, 1989, tai Enrico Beltrametti, Maciej Mączyński, ”On a characterization of classical and nonclassical probabilities”, Journal of Mathematical Physics $\boldsymbol{32}$ (1991) 1280-1286.

[23] R.F. Werner, ”Quantum states with Einstein-Podolsky-Rosen correlations admitting a hidden-variable model”, Physical Review $\boldsymbol{40}$ (1989) 4277.

[24] Alkuperäinen muotoilu: If, without in any way disturbing a system, we can predict with certainty (i.e., with probability equal to unity) the value of a physical quantity, then there exists an element of physical reality corresponding to this physical quantity.

[25] Alkuperäinen muotoilu: On the other hand, since at the time of measurement the two systems no longer interact, no real change can take place in the second system in consequence of anything that may be done to the first system. This is, of course, merely a statement of what is meant by the absence of an interaction between the two systems.

[26] D. Bohm, Quantum Theory, Prentice Hall, 1951.

[27] EPR-paradoksilla tarkoitetaan loogista ristiriitaa, joka syntyy kun kvanttimekaniikkaa (QM) täydennetään ehdoilla (R) ja (L). Looginen ristiriita voidaan purkaa monella tavalla ja tapauksessa $(QM)\&(R)\&(L)\Rightarrow\perp$ kaikkia vaihtoehtoja on tutkittu laajasti. Luottamus kvanttimekaniikkaan $(QM)$ on kuitenkin vahva, joten vaakalaudalla ovat ehdot $(R)$ ja $(L)$.

[28] A. Aspect, J. Dalibard, G. Roger, ”Experimental Test of Bell’s Inequalities Using Time-Varying Analyzers”, Physical Review Letters $\boldsymbol{49}$ (1982) 1804-1807.

[29] G. Weich, T. Jennewein, C. Simon, H. Weinfurter, and A. Zeilinger, ”Violation of Bell’s Inequality under Strict Einstein Locality Conditions”, Physical Review Letters $\boldsymbol{81}$ (1998) 5039-5044.

[30] M.A. Rowe et al, ”Experimental violation of a Bell’s inequality with efficient detection”, Nature $\boldsymbol{409}$ (2001) 791-794.

[31] Kysymyksessä on epäyhtälön (4.2) munnelma.

[32] Systeemien ei välttämättä tarvitse olla identtisiä. Riittää kun niillä voi olla kopioitavat ominaisuudet, esimerkiksi tietyt spinominaisuudet.

[33] C. Bennet, G. Brassard, C. Crépeau, R. Jozsa, A. Peres, W. Wooters, ”Teleporting an unknown quantum state via dual classical and Einstein-Podolsky-Rosen channels”, Physical Review Letters $\boldsymbol{70}$ (1993) 1895-1899.

[34] D. Bouwmeester, J.-W. Pan, K. Mattle, M. Eibl, H. Weinfurter, A. Zeilinger, ”Experimental quantum teleportation”, Nature $\boldsymbol{390}$ (1997) 575-579.

[35] D. Boschi, S. Branca, F. De Martini, L. Hardy, S. Popescu, ”Experimental realization of teleporting an unknown pure quantum state via dual classical Einstein-Podolsky-Rosen channels”, Physical Review Letters $\boldsymbol{80}$ (1998) 1121- 1125.

[36] Merkitsemme tilojen systeemikohtaisia alaindeksejä näkyviin vain tarvittaessa.

[37] Nykyteknologialla tämä hallitaan jopa sateliittietäisyyksillä säätilasta riippumatta: M. Mastriani, S. S. Iyengar, L. Kumar, ”Satellite quantum communication protocol regardless of the weather”, Optical and Quantum Electronics $\boldsymbol{53}$ (2021) 181 (14).

[38] Merkitsemme taas esim. $|{+\; – +}\rangle=|{+}\rangle_1|{- }\rangle_2|{+}\rangle_3= |{+}\rangle_1\otimes|{- }\rangle_2\otimes|{+}\rangle_3$.

[39] Koska vektorit $\phi$ ja $z\phi, |z|=1$, edustavat samaa tilaa, niin matriiseiksi $U_x, U_y, U_z$ voidaan valita myös Paulin spin matriisit $\sigma_1,\sigma_2,\sigma_3$.

[40] Foundations of Physics $\boldsymbol{29}$ (1999) 615-630. Ks. myös Azhar Iqbal, Derek Abbott artikkelissa ”A game theoretical perspective on the quantum probabilities associated with a GHZ state” Quantum Information Processing (2018) 17:313.

[41] Heidän keskustelujaan ovat raportoineet mm. Galileo Galilei teoksessa Dialog Concerning the Two Chief World Systems (1632), Joseph Maria Jauch teoksessa Are quanta real ? A Galilean dialogue (1973), sekä Kalervo Vihtori Laurikainen teoksessa Tieteen Giljotiini (1987).

[42] Tarkastelu yleistyy helposti $N$:lle identtiselle systeemille. Tässä asia kuitenkin sivuutetaan.

[43] Ääretönulotteisessa tapauksessa tarvitaan taas matemaattista hienosäätöä, johon ei tässä puututa.

Kirjoittaja

Pekka Lahti

dosentti kvanttimekaniikan perusteisiin erikoistunut eläköitynyt tutkija ja opettaja Turun yliopisto

Kirjoittaja

Kvanttimekaniikan peruskysymyksiä: yhdistetyt systeemit ja kvanttikietoutuminen

1. Teoreettinen lähtökohta

2. Kubittipari

3. Kvanttikietoutuminen

4. Kvanttikietoutuminen ja Bellin epäyhtälöt

4.1 Epäyhtälöiden todennäköisyysteoreettinen muotoilu

4.2 EPR argumentti

5. Kaksi sovellusta

5.1 Kvanttikopionti

5.2 Kvanttiteleportaatio

5.3 Eräs peli

6. Identtiset systeemit

7. Lopuksi

Kirjoittaja

Hae artikkeleita

Arkistot

Viimeisimmät

MAOLin syysliittokokous 2024 – valmistautumista juhlavuoteen 2025

Årets lärare 2024: I mitt Matteland, del 3

Marraskuun pulmat 2024: Kamelimatikkaa

OpenSCAD – 3D-kappaleita ohjelmoimalla

Mahtavaa matematiikkaa 2024: Sankaku-tehtävien laajennus

TILAA UUTISKIRJE

Kirjoittaja

1. Teoreettinen lähtökohta

2. Kubittipari

3. Kvanttikietoutuminen

4. Kvanttikietoutuminen ja Bellin epäyhtälöt

4.1 Epäyhtälöiden todennäköisyysteoreettinen muotoilu

4.2 EPR argumentti

5. Kaksi sovellusta

5.1 Kvanttikopionti

5.2 Kvanttiteleportaatio

5.3 Eräs peli

6. Identtiset systeemit

7. Lopuksi

Kirjoittaja

Jaa artikkeli

Lisää aiheesta

Matematiikkataikurit osa 2: Martin Gardner

Kaunista dataa

Hae artikkeleita

Arkistot

Viimeisimmät

MAOLin syysliittokokous 2024 – valmistautumista juhlavuoteen 2025

Årets lärare 2024: I mitt Matteland, del 3

Marraskuun pulmat 2024: Kamelimatikkaa

OpenSCAD – 3D-kappaleita ohjelmoimalla

Mahtavaa matematiikkaa 2024: Sankaku-tehtävien laajennus

TILAA UUTISKIRJE

Seuraa meitä