Mahtavaa matematiikkaa 2024: Sankaku-tehtävien laajennus

Hyvää Mahtavaa matematiikkaa -päivää 2024! Tänä vuonna MAOL tarjoaa teemapäivään nämä sankaku-teemaisia pulmatehtävät, päässälaskukilpailun 7. luokkalaisille (vielä perjantainakin ehtii osallistua!) ja AmmatikkaTOP-matematiikkakilpailun ammattikouluille.

Voit tutustua kaikkeen teemapäivän materiaaliin osoitteessa mahtavaamatematiikkaa.fi ja MAOLin aiempien vuosien materiaaleihin materiaalipankissamme.

Sankaku-tehtävien laajennus

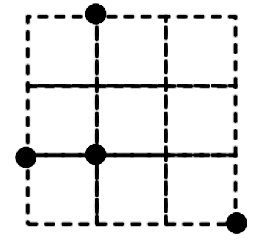
Sankaku voi viitata elokuvaan tai punk-albumiin. Samaa nimeä käytetään myös Naoki Inaban kehittämistä geometrian tehtävistä. Ne rakentuvat neliöruudukkoon sijoitetun pistejoukon varaan. Yksi yksinkertaisimmista on kuvassa. Siinä on piirrettävä kolmio, jonka kärkipisteet valitaan annetuista neljästä pisteestä ja jonka pinta-ala on yksi pinta-alayksikkö (lähteenä Sarah Carterin blogi Sankaku Puzzles osoitteessa https://mathequalslove.net/sankaku-puzzles/). Tästäkin asetelmasta saataisiin irti paljon enemmän.

Tehtäviä

1. Ratkaise edellä esitetty sankaku-tehtävä. 

2. Piirrä muut kolmiot, jotka voidaan virittää kuvassa annettujen pisteiden varaan.

3. Mitkä ovat niiden pinta-alat?

4. Mikä on pinta-alaltaan pienin kolmio, joka voidaan muodostaa, kun neljä pistettä voidaan sijoittaa vapaasti kolme kertaa kolme -ruudukkoon?

5. Entä suurin? Kuinka monta sellaista voidaan piirtää pisteiden eri asennoilla? Entä kuinka monta erimuotoista?

6. Voidaanko neljä pistettä sijoittaa kolme kertaa kolme -ruudukkoon niin, että tehtävien 4 ja 5 ratkaisut saadaan samasta kuviosta? Jos ei niin, mikä on pinta-alaltaan suurin kolmio, kun kolme pistettä on sijoitettava niin, että muodostuu tehtävän 4 pienin kolmio ja neljäs piste saadaan sijoittaa vapaasti? 

7. Sijoita neljä pistettä kolme kertaa kolme -ruudukkoon niin, että muodostettavien kolmioiden pinta-alojen summa on mahdollisimman suuri. 

8. Entä pienin, kun mitkään kolme pistettä eivät saa olla samalla suoralla?

9. Onko mahdollista sijoittaa neljä pistettä 3×3-ruudukkoon niin, että mitkään kolme pistettä eivät ole samalla suoralla ja muodostuneista kolmioista on suorakulmaisia enemmän kuin yksi?

Dimension pulmasivujen ratkaisut julkaistaan MAOL ry:n jäsensivuilla. Näiden Mahtavaa matematiikkaa -pulmatehtävien ratkaisut voit katsoa täältä, vaikka et olisikaan jäsen.

Dimensio-lehden edelliset sankaku-pulmat: Puu­haa vii­mei­sel­le vii­kol­le en­nen lo­mia: Zu­kei- ja san­ka­ku-pul­mia (21.5.2024)

Lue myös muut Dimension verkkolehdessä ilmestyneet pulmatehtävät