Pyy on piin yleistys

Ympyrän kehän ja halkaisijan suhteelle otti käyttöön merkinnän ”π” walesilainen William Jones vuonna 1706 [1]. Nykyään piin likiarvo on laskettu sadan biljoonan desimaalin tarkkuudella [2]. Koulumatematiikasta pii on tuttu, mutta oletko koskaan tullut ajatelleeksi, että piin käsitteen voisi yleistää? Jos seuraava ei ole mielestäsi vakavaa ja ”oikeaa” matematiikkaa, niin on se ainakin matematiikan puolustamisen [3] toisen käskyn ”leiki matematiikalla” mukaista toimintaa.

Piin merkitys ympyrälaskuissa perustuu siihen, että kaikki ympyrät ovat yhdenmuotoisia. Vastinviivojen pituuksien suhde on siis sama kaikissa ympyröissä, erityisesti kehän ja halkaisijan. Mitä muita vastaavia kuvioita on? Voisiko niitä luonnehtia jollain piitä vastaavalla suhdeluvulla?

Vaikka emme ole vielä edes määritelleet piin yleistystä [4], voimme antaa sille nimen pyy. Tämä ei ole ihan niin hullua, kuin ensikuulemalta saattaa kuulostaa. Onhan sanalla ’pii’ kaksi muutakin merkitystä. Alun perin se on tarkoittanut hammasta tai piikkiä. Muissa kuin matemaattisissa mielikuvissa pii liittyykin haravaan. Lisäksi ’pii’ voi tarkoittaa myös alkuainetta. Sana ’pyy’ voisi tarkoittaa vastaavasti piin yleistystä sen ohella, että merkityksenä on myös pieni metsäkanalintu (tetrastes bonasia).

Säännölliset monikulmiot voisivat olla niitä kuvioita, joihin sovellamme ensiksi ajatustamme matemaattisesta pyystä. Otetaan tasasivuinen kolmio, jonka sivu on yksi. Sen piirin pituus on 3. On vain yksi jana, johon piiriä voi verrata: korkeusjana (kuva 1, vasen osakuva). Pyy on nyt

$$3 ∶ \frac{\sqrt3}{2} ≈ 3,46.$$

Sama on tilanne neliössä. Neliön pyy on $4 ∶ \sqrt2 ≈ 2,83$

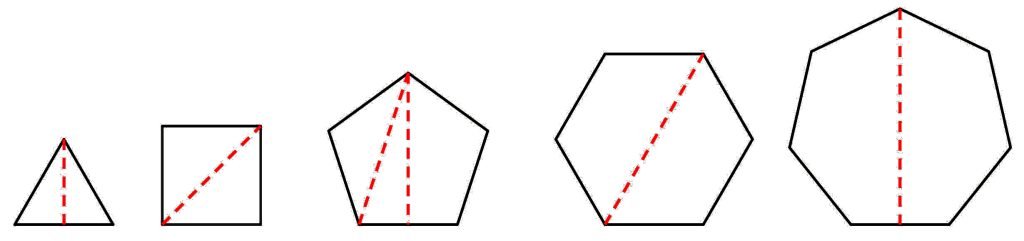
Entä sitten säännöllinen viisikulmio? Piiriä voitaisiin verrata nyt kahteen eri janaan: lävistäjä tai ”korkeusjana” eli ympäri piirretyn ympyrän säteen ja apoteeman summa (kuva 1, keskimmäinen osakuva). ”Korkeusjana” on parempi, koska yhtäältä se kulkee keskipisteen kautta niin kuin kolmion ja neliön kohdalla käyttämämme janat ja toisaalta lävistäjiä on useita erilaisia niissä säännöllisissä monikulmioissa, joissa kulmia on enemmän kuin viisi. Viisikulmion pyy on siten

$$\frac{5}{\frac{\frac{1}{2}}{\tan 18^{\circ}}} = \frac{5}{\frac{\frac{1}{2}}{\frac{1}{5}\sqrt{25-10\sqrt{5}}}} \approx 3,25$$

Säännöllisen kuusikulmion lävistäjistä valitsemme pitemmän, koska se on samalla ympäri piirretyn ympyrän halkaisija. Pyy on nyt

$$\frac{6}{2}=3$$

Jo näistä esimerkeistä näkyy, että säännöllisen monikulmion pyy on piirin suhde

1°     monikulmion ympäri piirretyn ympyrän säteen ja apoteeman summaan, kun kulmien lukumäärä on pariton

2°     pisimpään lävistäjään, joka on sama kuin ympäri piirretyn ympyrän halkaisija, kun kulmien lukumäärä on parillinen.

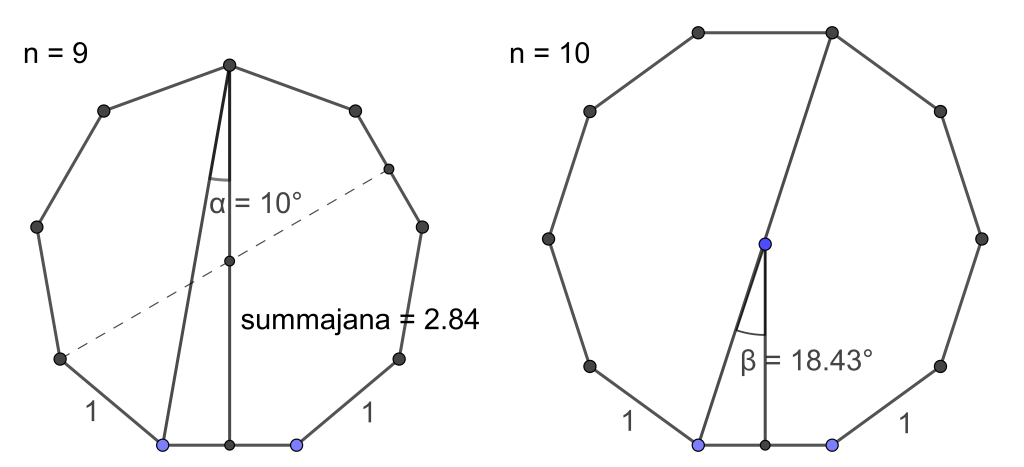
Edellisessä tapauksessa on laskettava mainitun summajanan pituus ja jälkimmäisessä tapauksessa monikulmion ympäri piirretyn ympyrän halkaisija. Ne saadaan helpoimmin kulmien avulla (kuva 2): summajana $= 0.5 \tan (90^{\circ} /n)$ ja halkaisija $= 2 \cdot 0,5 / \sin(180^{\circ}/n)$.  Niistä voidaan sitten laskea pyyarvot (taulukko).

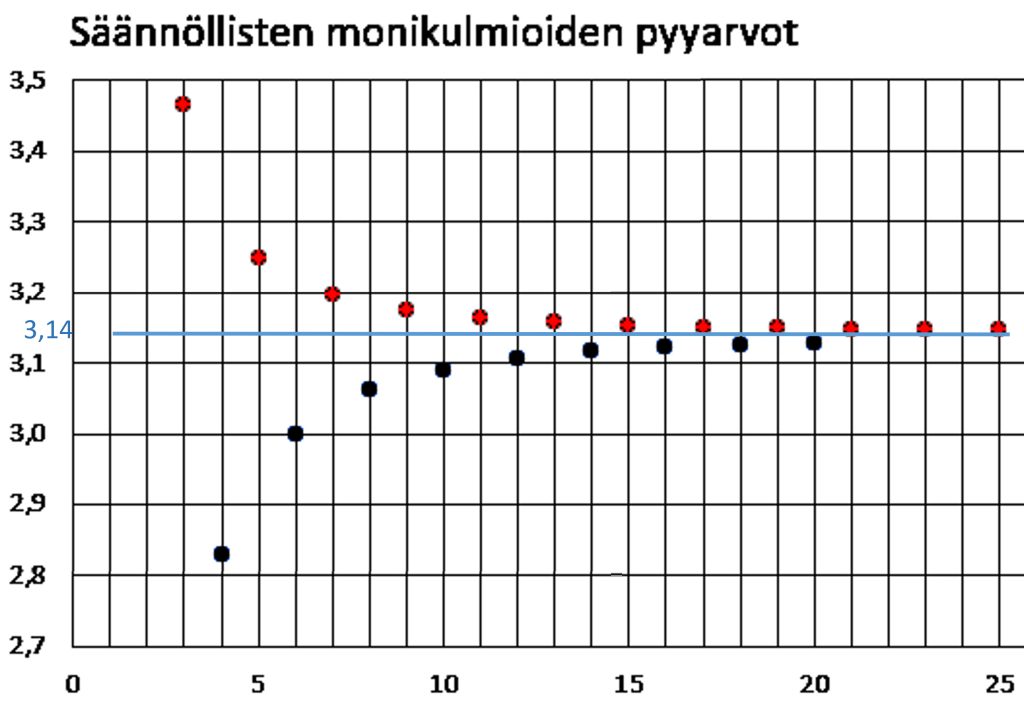
Taulukko: Säännöllisten monikulmioiden pyyn arvoja

n	pyy
3	$3 : \sqrt{3}/2 \approx 3,46$
4	$4 : \sqrt{2} \approx 2,83$
5	$\frac{5}{\frac{\frac{1}{2}}{\tan 18^{\circ}}} \approx 3,25$
6	6 : 2 = 3
7	$7 : \frac{7}{\frac{\frac{1}{2}}{\tan 12\frac{6}{7}^{\circ}}} \approx 3,20$
8	$\frac{8}{\frac{1}{\sin 22,5^{\circ}}} \approx 3,06$
9	$\frac{9}{\frac{\frac{1}{2}}{\tan 10^{\circ}}} \approx 3,17$
10	$\frac{10}{\frac{1}{\sin 9^{\circ}}} \approx 3,09$
11	$\frac{11}{\frac{\frac{1}{2}}{\tan \frac{90}{11}^{\circ}}} \approx 3,16$
12	$\frac{12}{\frac{1}{\sin \frac{180}{12}^{\circ}}} \approx 3,11$

Sama periaate soveltuu tietysti kaikkiin yhdenmuotoisiin kuvioihin, mutta mitä epäsäännöllisemmästä kuviosta on kyse, sitä hankalampaa on valita jana, johon piiriä sopii verrata, jotta piirin ja valitun janan suhde luonnehtisi kuviota edes vähänkään. Mitä esimerkiksi kertoisi kuperasta monikulmiosta piirin ja mahdollisimman kaukana toisistaan olevien kahden kärkipisteen yhdistysjanan suhde?

Artikkelikuvassa on harava, pii, pii, monta piitä piissä ja pyy.

Lähteitä ja lisää luettavaa

[1] Kangasniemi, Tuomas: Miten ihmeessä ympyrän kehän ja halkaisijan suhde sai symbolikseen π? Tekniikka ja talous 14.3.2021/14.3.2024. https://www.tekniikkatalous.fi/uutiset/miten-ihmeessa-ympyran-kehan-ja-halkaisijan-suhde-sai-symbolikseen-historian-ensimmainen-pii-julkaistiin-1706-kuva-selvitimme-koko-tarinan-piin-paivan-143-kunniaksi/cb699bf8-e359-489f-b8de-a651f74229bb

[2] Pi calculated to 105 trillion digits, smashing world record, Live Science 15.3.2024 osoitteessa https://www.livescience.com/physics-mathematics/mathematics/pi-calculated-to-105-trillion-digits-smashing-world-record

[3] Korhonen, Hannu: Matematiikanpuolustaja (Dimensio 28.3.2021)

[4] Idea on peräisin teoksesta Ellenberger, Jordan: Muoto: Aivan kaiken kätketty geometria; Terra Cognita, 2023. Katso kirjaesittelyä Kirjallisuutta: Muoto (Dimensio 9.4.2024)