Sinin, kosinin ja tangentin historiaa

Yleistä

22.7.2025

Trigonometria tulee kreikan sanoista trígōnos eli kolmekulmainen ja métron eli mitata, jolloin sana trigonometria voidaan suomentaa kolmiomittaukseksi. Suorakulmaiseen kolmioon liitettävät sini, kosini ja tangentti ovat matematiikasta kaikille tuttuja trigonometrian perusasioita, mutta miksi niitä nimitetään siniksi, kosiniksi ja tangentiksi? Mikä merkitys niillä on ollut ja mikä on niiden historia?

Tähtien tutkimista

Muinaisessa Babyloniassa (1800 eaa.) tutkittiin tähtitaivasta, koska sitä pidettiin jumalien asuinpaikkana. Silmin havaittavat taivaankappaleet: kuu (sin), mars (nergal), merkurius (nabu), jupiter (marduk), venus (ishtar), saturnus (ninurta) ja aurinko (shmash), nimettiin jumalien mukaan. Näistä nimistä periytyvät myös viikonpäivien nimet. Esimerkiksi maanantai on kuunpäivä ja sunnuntai on auringon päivä. Kuun jumala Suen tai Sin, joka tunnettiin myös nimellä Nanna tai Nanna-Suen oli erityisen tärkeä maanviljelyksessä ja karjanhoidossa. Kolmiomatematiikan perusta luotiin Babyloniassa viljelyalojen ja rakennusten mittaamista varten, vaikka siitä on jäänyt vähän kirjallisia dokumentteja. Sini-sana ei ole periytynyt matematiikkaan babylonialaisesta kuun jumalasta Sin, vaikka hyvin voisi olla. Babyloniassa arvioitiin, että ”auringon liike maan ympäri” tapahtuu vuoden aikana 360 päivässä. Vastaavasti kuukaudet tulevat kuun kierrosta, jossa yksi kuun kierto tapahtuu noin 30 päivässä. Luku 360 on myös hyvä luku ympyrän jaollisuutta ajatellen. Babylonialaiset jakoivat ympyrän myös 360 osaan, josta tulevat käyttämämme asteluvut. Jos 360 asteen ympyrä jaetaan kuuteen osaan, niin saadaan aikaiseksi kuusi tasasivuista kolmiota ympyrän sisälle. Tasasivuisessa kolmiossa 60 asteen kulmalla ympyrän säde on yhtä pitkä kuin ympyrän kehällä oleva jänne. Tämä havainto oli erittäin hyödyllinen.

Ensimmäiset kirjalliset pohdinnat pyramidin kaltevuuden ja pyramidin mittojen suhteesta ovat löydettävissä Rhidin papyryksesta (1650 eaa.) Egyptistä, vaikka suurin tarve geometrian käyttämiselle Egyptissä oli maanviljelyksessä. Kun Niili-joki tulvi, niin kirjureiden piti merkitä käyttämättömät viljelysalueet ylös.

Kreikkalaiset ajattelivat, että maa on kiinteä piste maailmankaikkeudessa ja taivas on puolipallon muotoinen, jossa sijaitsevat tähdet, kuu ja aurinko. Kreikkalaiset omaksuivat babylonialaisten 360 osan asteet, jotka he sitten jakoivat vielä 60-osiksi (pars per minuta) ja 3600-osiksi (pars per sekunda), josta tulevat meille tutut ajan yksiköt. Minuta tarkoittaa ensimmäistä ja secunda toista, pars per minuta on ensimmäinen pieni osa ja pars per sekunda on toinen pieni osa. Radiaaniasteet tulivat mukaan vasta 1700-luvun tieteellisissä julkaisuissa, joissa tutkittiin jaksoittaista ja ympyräliikettä, jolloin pidettiin kätevänä ilmoittaa kulmat ympyrän kaaren pituutena. Radiaaniasteet on otettu mukaan SI-järjestelmään tasokulman yksiköksi, mutta muuten babylonialaisten ja kreikkalaisten ympyrän 360 osan asteet ovat jääneet elämään. Muita kulman asteita ovat esimerkiksi ranskalaisten käyttämä 400 osan gooniasteikko ja tykistön käyttämä 6283 osan piiruasteikko.

Kreikkalaisilta ovat peräisin myös suorakulmion nimitykset hypotenuusa ja kateetti. Hypotenuusa (πλευρά) tarkoittaa kreikassa suorakulman vastaista viivaa ja kateetti (Κάθετος) vastaavasti tarkoittaa suorakulman jalkoja eli suorakulman viereisiä viivoja suorakulmaisessa kolmiossa. Pythagoras (582–496 eaa.) esitti ensimmäisenä, että maapallo on pallon muotoinen ja koko maailmankaikkeus (kreikaksi kosmos) on järjestyksessä ja tasapainossa, aivan kuin kokonaisluvut ja niiden väliset suhteet. Eukleides kokosi kreikkalaisten geometrian havainnot yksiin kansiin vuonna 300 eaa. julkaisemalla geometrian oppikirjan Elementa eli alkeet.

Sen ajan merkittävin tähtitieteilijä Hipparkhos Nikealainen (190–120 eaa.) oivalsi, että mikä tahansa kolmio voidaan piirtää ympyrän sisälle. Hipparkhos esitti, että tähden etäisyys toisesta tähdestä voidaan ilmaista jänteen avulla, kun tunnetaan kaarta vastaava kulma. Niinpä hän julkaisi jännetaulukon, jossa oli noin 20 jänteen pituutta eri asteluvuilla eli käytännössä ensimmäinen sinitaulukko. Näistä ansioista häntä on alettu kutsua ”trigonometrian isäksi”. Arvellaan, että laskiessaan jänteen pituuksia Hipparkhos käytti 3600 yksikön säteen arvoa ympyrässään, jolloin jänteen pituus annettiin myös kokonaislukuna. Desimaalilukuja ei vielä tuolloin tunnettu. Näitä tietoja Hipparkhos tarvitsi, kun hän laski kuun ja auringon kiertoratojen epäkeskisyyttä ympyrän kehälle piirretyillä suorakulmaisilla kolmioilla. Hipparkhos oli ensimmäinen, joka käytti tähtitaivaan kappaleiden paikan määrittämiseen pituus- ja leveysasteita. Lisäksi Hipparkhos julkaisi tähtiluettelon ja osasi laskea oikein kuun kiertoajan ja vuoden pituuden, sekä osasi ennustaa auringonpimennyksiä.

Kuva 1: Kulman mittaaminen sinikvadrantilla, jossa asteikolta voitiin lukea kulmaa vastaava sinin arvo. Sinikvadrantilla mitattiin taivaankappaleiden sijaintia taivaalla. Lähde: Wikipedia [10]

Ptolemaios (150 jaa.) myöhemmin teki tarkemman jännetaulukon ja kokosi siihenastisen tähtitieteellisen tiedon julkaisemalla teoksen Mathematike Syntaxis. Nämä kirjalliset tiedot levisivät myöhemmin Intiaan ja Arabiaan. Myös kuun ja auringon liikettä mitattiin. Auringon meridiaanikulma voitiin mitata antiikin kreikassa kvadrantilla, jossa tapin varjo heijastettiin 90°-asteikolle. Siitä tulee kulmamittauslaitteen nimitys kvadrantti, joka tarkoittaa neljäsosaympyrää. 900-luvulla arabialaiset käyttivät sinikvardanttia (ks. kuva 1), jonka avulla sinin arvo voitiin määrittää sivussa olevilta asteikolta, kun kulma mitattiin. Tästä kehittyi myöhemmin merenkulkijoiden käyttämä kvadrantti, jossa mukana oli luotisuora. Luotisuora oli ongelmallinen, jos meri ei ollut tyyni, joten mittaustekniikkaa on ollut pakko kehittää. Vuonna 1731 John Hadley kehitti sekstantin, jossa mitattiin horisontin ja taivaan kappaleen välinen kulma liikuteltavan peilin avulla (ks. kuva 2a).

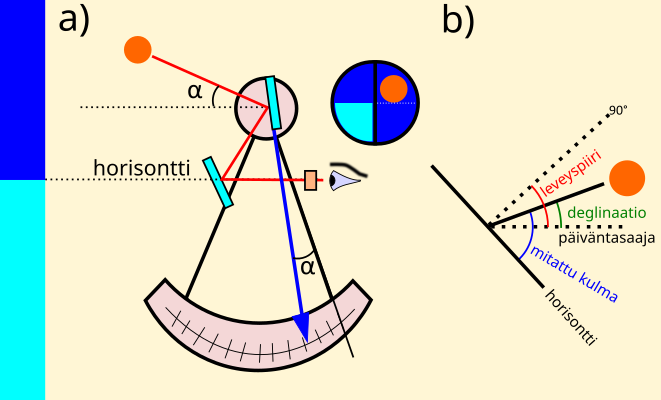
Kuva 2: John Hadleyn sekstantti vuodelta 1731. Katsoja laittoi sekstantissa horisontin ja taivaalla olevan kohteen, kuten tähti tai aurinko, vierekkäin kaksiosaiseen okulaariin liikuteltavan peilin avulla, jonka jälkeen horisontin ja taivaalla olevan kohteen välinen kulma voitiin lukea asteikolta, johon liikuteltavasta peilistä lähtevä nuoli osoitti. Jos katsottiin aurinkoon, lisäksi tarvittiin himmennetty lasi peilin eteen tai lappu silmän eteen. Piirustus: Tuomo Riekkinen.

Esimerkiksi mittaamalla kulma sekstantilla horisontin ja pohjantähden välillä saamme suoraan leveysasteen pohjoisella pallonpuoliskolla. Pohjantähti osoittaa myös suunnan pohjoiseen. Jos taas mittaamme horisontin ja auringon korkeimman paikan välisen kulman, leveysaste voidaan laskea kaavalla (ks. kuva 2b):

$ Leveysaste = 90° – mitattu kulma + deglinaatio \qquad (1) $

Auringon korkein paikka on ajan hetkellä, jolloin auringon varjo on lyhyin. Deglinaation arvo eli auringon sen hetkinen poikkeama päiväntasaajalta saatiin almanakasta, joita alettiin painamaan Euroopassa heti kun kirjapaino oli keksitty 1400-luvulla. Pituusasteen mittaaminen on ollut hankalampaa johtuen maapallon pyörimisestä. Auringon korkeimman paikan lisäksi tarvitaan tarkka aika, joka saadaan kellosta, jota nimitetään kronometriksi. Tällainen kello rakennettiin vasta vuonna 1759. Ennen tätä pituuspiiri yritettiin selvittää laivan nopeuden avulla. Laivan nopeus määriteltiin mittaamalla matka köyden eli niin sanotun lokiliinan avulla, jossa oli solmuja, ja aika mitattiin tiimalasin avulla. Siksi laivan nopeus vielä nykyäänkin mitataan solmuina. Pitkällä matkalla virheiden suuruus kasvoi ja samoin mahdollisuus joutua haaksirikkoon. Tarkan kellon eli kronometrin avulla tämä ongelma poistui. Jokainen tunnin poikkeama vertailuaikaan eli Greenwichin aikaan tarkoitti 360°:24 = 15° pituuspiireittäin. Eli esimerkiksi auringon ollessa paikallisesti korkeimmillaan kello näyttää Greenwichin aikaa klo 14:00, eli ero paikalliseen aikaan on silloin tasan kaksi tuntia. Tällöin laiva on paikassa 30 astetta länteen. Jos kello näyttäisi aikaa klo 10:00, laiva olisi paikassa 30 astetta itään.

Sanojen alkuperä

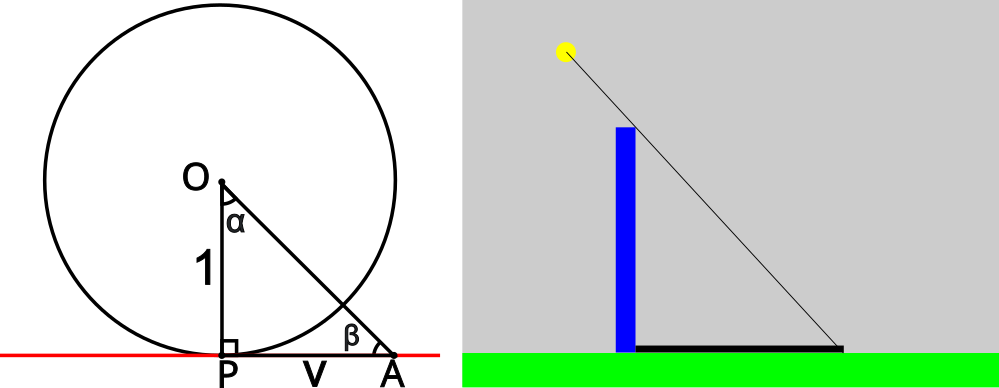
Sini-sanan alkuperän katsotaan olevan Intiassa, jonne kreikkalaisten alkeelliset tiedot trigonometriasta levisivät Aleksanteri Suuren valloitusten mukana. Myös intialaiset tutkivat tähtiä ja kehittivät omia jännetaulukoita. Sanskritin sana jīva tai jyā tarkoittaa jousipyssyn jännettä. Kun merkitsemme ympyrän sädettä OA yhdellä, niin puolijännettä vastaava kulman alfa sini eli jyā on (Katso kuva 3)

$ juā\ \alpha=\frac{PA}{OA}=\frac{x}{1}=x \qquad (2) $

Intiassa kulman sini eli jyā siis tarkoitti jousen kaarikulman vastaavaa jänteen pituutta. Vastaavasti sana kojyā tai koti-jyā tarkoittaa kosinia, joka on sinin komplementtikulma eli silloin määrittelemme: kojyā β = x. Komplementtikulmilla tarkoitetaan kulmia, joiden summa on 90° eli α + β = 90°. Matemaattisissa julkaisuissa jyā tarkoitti Intiassa kulman vastaista sivua ja kojyā tarkoitti kulman viereistä sivua.

Kuva 3: Onko jousen jänteellä ja ympyrän jänteellä jotain yhteistä? Kun halutaan selvittää jousen jänteen AB pituus, niin meidän pitää käytännössä jakaa tasakylkinen kolmio OAB kahdeksi suorakulmaiseksi kolmioksi. Yksikköympyrässä kulman alfa sini on sama kuin puolijänteen pituus. Kuvat: Pixabay ja Tuomo Riekkinen.

700-luvulla intialainen matemaatikko ja tähtitieteilijä Brahmagupta teki tarkat taulukot sinin arvosta eri kulmilla. Brahmagupta käytti julkaisuissaan sanoja jyā ja kojyā, tarkoittaen siniä ja kosinia. Kun intialaisten tekstit käännettiin arabiaksi, niin jyā eli kulmaa vastaava jänne sana käännetiin virheellisesti merkityksettömäksi sanaksi jiba ja siksi lyhennettiin muotoon jb, josta myöhemmät arabialaiset kirjoittajat sen väänsivät muotoon jaib, jolloin se tarkoitti ”rintaa” tai ”taitosta”. Oliko ajatus, että jousipyssyn jänne koskettaa rintaa ja syntyy suorakulmainen kolmio? No, siitä ei ole tietoa. Sini-sanan alkuperä on Intiassa, mutta arabialaiset myös taulukoivat (noin 800 jaa.) sinin lisäksi kosinin, tangentin, kotangentin, sekantin ja kosekantin arvoja. Kun arabialaisen al-Khwārizmīn trigonometrinen teos käännettiin 1200-luvulla latinaksi Gerad Cremonalaisen toimesta, niin arabian rinta-sanaa jaib vastaava ilmaisu latinassa on sinus, joka latinankäännöksessä tarkoittaa ”toogan roikkuvaa taitosta rinnan yli” ja sieltä on peräisin meidän käyttämämme termi sini. Kosini tulee latinankielisestä sanasta complementi sinus eli sinin komplementtikulma.

Tangentti-sanaan ei liity niin paljon historiaa ja väärinymmärryksiä kuin sini-sanaan. Tangentti käsitteenä oli jo antiikin Kreikassa. Euclid ja Archimedes käyttävät termiä tangentti julkaisuissaan, vaikka itse tangentin arvojen laskeminen ja taulukoiminen jäi arabeille. Tangentti tarkoitti antiikin kreikassa suoraa, joka sivuaa ympyrää ja sen merkitys on pysynyt samana näihin päiviin asti. Kun tälle suoralle piirretään suorakulmainen kolmio (ks. kuva 4), jossa kolmion toinen kateetti on ympyrän säde ja toinen tuntematon mitta v, niin saamme määriteltyä tangentin.

$ \tan\ \alpha=\frac{PA}{OP}=\frac{v}{1}=v \qquad (3) $

Tässä ympyrän säde on yksi, jolloin tangentti kulmasta alfa tarkoittaa siis tangenttisuoralla olevaa mittaa v, jossa v tarkoitti alun perin varjon pituutta. Arabialainen matemaatikko Habash al-Hasib al-Marwazi (766–869 jaa.) tutki pylvään varjon pituutta ja laati taulukoita tangentista, jonka julkaisuista sana tangentti on periytynyt myös Eurooppaan. Myös tangentin komplementtikulmaa eli kotangenttia taulukoitiin eli havaitaan, että cot β = v.

Kuva 4: Tangentin alkuperäinen nimitys perustuu tangenttisuoraan, joka sivuaa ympyrää. Arabiassa tangentilla tarkoitettiin kulmaa α vastaavan varjon pituutta v, jota tutki sitä varten perustettu matematiikan osa-alue. Piirustus: Tuomo Riekkinen.

Kolmiomittauksen synty

Aluksi sini ja kosini liittyivät pelkästään taivaankappaleiden paikan mittaukseen. Vuonna 1464 saksalainen matemaatikko Johannes Müller julkaisi teoksen De Triangulis Omnimodis, jossa hän kuvasi kaikki siihen asti keksityt trigonometriset lausekkeet, joita hän havainnollisti kuvin ja esimerkein. Teos sai suuren suosion ja levisi laajalle, lisäksi teoksesta tehtiin monta käännöstä. 1600-luvulla hollantilaiset kehittivät näiden tietojen avulla avulla kolmiomittauksen, joka perustuu jo Johannes Müllerin kirjassa olleeseen sinilauseeseen.

$ \frac{a}{b}=\frac{\sin\alpha}{\sin\beta} \qquad (4) $

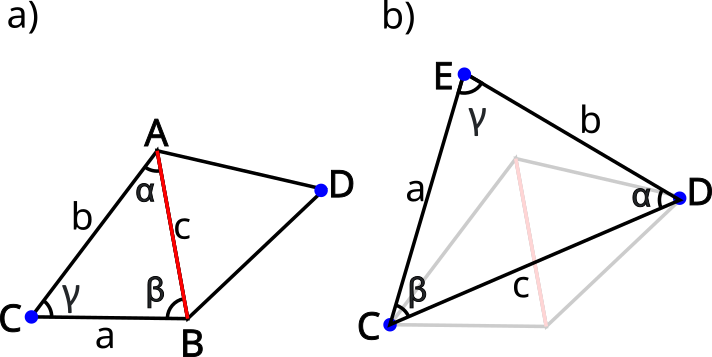
Mitattava maaston alue peitetään kiintopisteillä, jotka muodostavat kolmioiden verkoston. Kun tunnetaan yhden kolmion sivun pituus ja kolmioiden kulmat, niin voidaan laskea muiden kolmioiden sivun pituudet tarkasti. Aluksi mitattiin noin kolmen kilometrin pituinen perusviiva AB (ks. kuva 5a), jonka tarkkuus oli jo 1900-luvulla millimetrin luokkaa. Perusviivan mittauksessa käytettiin jäykkiä ja kalibroituja tankoja, jotka myöhemmin korvattiin invarlangoilla. Perusviiva näkyi kahteen viivan molemmilla puolilla oleviin torneihin C ja D, josta suoritettiin kulman mittaus. Myös perusviivan päissä olevat kulmat mitattiin. Perusviiva ja tornit muodostivat kolmiot, joiden sivun pituudet AD ja AC voitiin laskea sinilauseen (3) avulla. Kun matkat AD ja AC olivat tiedossa ja näiden välinen kulma γ (ks. kuva 5b), niin näiden kahden tornin välinen matka CD taas laskettiin kosinilauseen avulla, joka on muotoa:

$ c^2=a^2+b^2-2ab\cos\gamma \qquad (5) $

Kun kolmiosta CDE tunnettiin nyt yhden sivun pituus tarkasti eli CD, niin mittaamalla tornien välillä olevat kulmat α, β ja γ, voitiin sinilauseen (4) avulla laskea tornien väliset etäisyydet DE ja CE. Kun perustetaan seuraava torni niin että sieltä näkyy kaksi edellistä tornia, niin kolmioiden sivujen mittaa voidaan kuljettaa eteenpäin mittaamalla vain kolmioiden kulmia. Tyypillinen tornien välimatka kolmiomittauksessa oli noin 20–50 kilometriä. Välillä voitiin mitata uusi perusviiva maastoon ja tarkistaa ovatko mittaukset ja laskelmat pitäneet paikkansa.

Kuva 5: Kolmiomittauksen periaate. a) Aluksi perusviivan AB pituuden ja kulmien avulla määriteltiin kahden tornin välinen etäisyys CD. b) Kun mukaan otettiin kolmas torni E, niin saatiin kolmio CDE, jonka kaikki puuttuvat sivun pituudet voitiin laskea sinilauseen avulla. Tätä mittaa kuljetettiin eteenpäin seuraavaan torniin muodostamalla uusia kolmioita ja mittaamalla kulmia. Piirustus: Tuomo Riekkinen.

Kun kolmiomittaus on valmis, niin kolmioverkko on sijoitettava vielä maanpinnalle oikeaan paikkaan ja asentoon tähtitieteellisten mittausten avulla. Kolmiomittauksen avulla on määritelty esimerkiksi Mount Everestin korkeus, osoitettu maan litistyneisyys ja on voitu piirtää tarkkoja karttoja 1700-, 1800- ja 1900-luvuilla.

Suomessa on tehty kolme suurta kolmiomittausta. Ensimmäinen oli vuosina 1736–1737, jolloin ranskalainen Maupertuis’n retkikunta teki mittauksia Torniojokilaaksossa. Nämä mittaukset liittyivät tieteelliseen kiistaan siitä, pitääkö Newtonin väite maan litistyneisyydestä paikkansa. Toinen kolmiomittaus oli niin kutsuttu Struven ketju, jossa kolmiomittaus tehtiin Mustaltamereltä Pohjoiselle jäämerelle. Mittaus liittyi maapallon koon määrittämiseen, mutta myös karttojen piirtämiseen. Suomessa mittaukset tehtiin vuosina 1830–1852. Kolmas kolmiomittaus liittyi Suomen peruskartan piirtämiseen ja mittaus ajoittui vuosille 1919–1987. Nykyään GPS-mittaus, ilmakuvaus ja satelliittipaikannus ovat korvanneet kolmiomittaukset. Muistona kolmiomittauksista ovat romahtaneet tornit ja reiät kalliossa. Samoin sini, kosini ja tangentti ovat löytäneet uusia käyttökohteita, kuten esimerkiksi kuvaamaan radioaaltoja, heilureita, vuorovesiä, sävelääniä ja sähkövirtoja. Näiden ilmiöiden pohja luotiin 1700-luvulla Newtonin ja Eulerin sarjakehitelmien avulla, sekä havainnosta, että trigonometriset funktiot voitiin määritellä yksikköympyrän avulla.