Spirolateraali – kierrekuvio

Matematiikkaa on mahdollista ruveta harrastamaan jo paljon ennen kouluikää. Yksi mahdollisuus ovat viivapiirrokset (spirolateraalit). Ne eivät ole pelkästään geometrisen havaintokyvyn kehittymistä edistävä älyllinen leikki, vaan kynällä piirrettyinä tukevat myös hienomotoriikan kehittymistä. Monipuolisimmillaan ne voivat johtaa hyvinkin monimutkaisiin kuvioihin ja matemaattisiin päätelmiin.

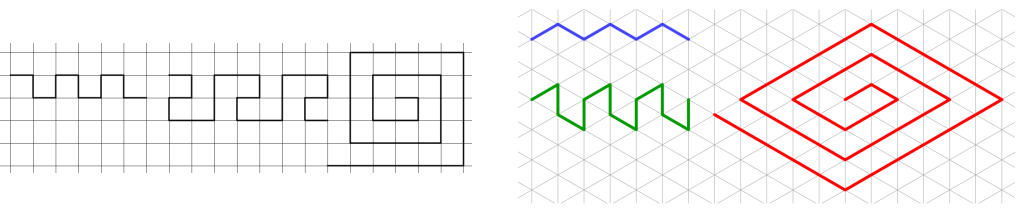
Yksinkertaisimmillaan kyse on murtoviivojen piirtämisestä ruutupohjalle: neliö- tai kolmioruudukkoon (kuva 1). Tässä vaiheessa ei ole tarpeen käyttää vielä mitään geometrisia ilmaisuja. Kyse on vain piirtämisestä, joka harjaannuttaa kuvioiden hahmottamista ja edistää geometrisen mielikuvituksen kehittymistä.

Miksi sitten nimittää murtoviivoja spirolateraaleiksi? Kyse on varmaankin siitä, että varsinkin matemaatikot ja matematiikan opettajat ovat tottuneet käsitteelliseen ajatteluun. Kohteilla, olivatpa ne sitten kuvia, lukuja, funktioita tai mitä tahansa, pitää olla nimi, jotta niistä voidaan puhua. Epämääräiset nimitykset, kuten mutkikas tai kulmikas viiva, tuntuvat sotivan matemaattista ajattelua vastaan. Turhaa, näennäistä täsmällisyyden tavoitteluako, kun kuvan aikaansaamisessa luulisi olevan riittävästi elämyksellistä palkkiota?

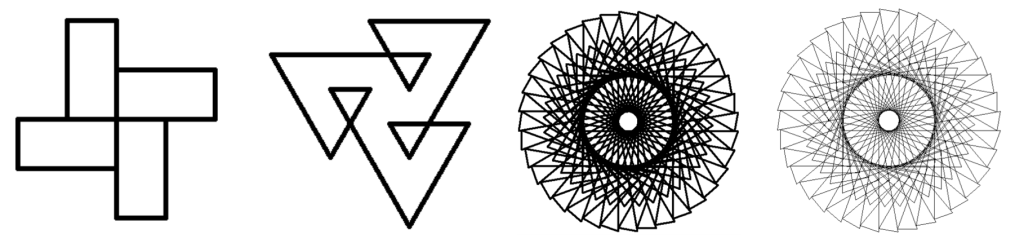
Nimi ”spirolateraali” on peräisin 1960-luvulta. Sen keksijä on englantilainen koulupoika Frank C. Odds [1], myöhempi kuuluisa sienitutkija. Kuvioista hän kirjoitti Martin Gardnerin rohkaisemana vuonna 1973 [2]. Gardner kirjoitti näistä sitten itsekin [3]. Spirolateraaleiksi nimitetään nykyään monenlaisia viivapiirroksia, myös monikulmioita (kuva 2).  Samankaltaisia kuvioita käytettiin paljon kilpikonnagrafiikkaharjoituksina [4] silloin, kun Logo-kieli oli runsaassa käytössä 1970–1990-luvuilla, nimittämättä niitä spirolateraaleiksi (kuva 3).

Odds kertoi nimen spirolateral viittaavan yhtäältä spiraaliin (engl. spiral) ja toisaalta tasokuvioon (lateral). Yhdyssanan kaltaisen nimen alkuosa viittaa kierteiseen muotoon (lat. spīra, kreikk.  σπεῖρα, speîra). Jälkiosa viittaa puolestaan täsmällisemmin tasokuvion sivuun (lat. latus, lateralis).  Suomalainen vastine voisi siis olla kierrekuvio, jos halutaan korostaa, että kyseessä ei ole mikä tahansa murtoviiva, vaan erityinen kuvioluokka.

Kun verrataan kuvan 2 kuvioiden Logo-ratkaisuja Riekkisen artikkelin [5] Scratch-koodeihin, niin havaitaan, miten paljon yhteistä ohjelmointikielillä on. Scratch-koodi voidaan kirjoittaa sellaisenaan esimerkiksi MSWLogon editoriin:

         repeat 4 [rt 90 repeat 2 [fd 50 rt 90 fd 100]]

         repeat 3 [fd 80 rt 120 fd 120 rt 120 fd 160 rt 120 fd 40 rt 120]

         repeat 36 [fd 320 rt 110 fd 40 rt 110 fd 280 rt 110 fd 80 rt 110 fd 160 rt 110]

Logon etuna on se, että esimerkiksi kahden vasemmanpuoleisen kuvan osien piirtämistä voidaan testata vaihe vaiheelta jo ennen kuin on tarvetta kirjoittaa ohjelmaa.

Yhden yksittäisen kuvion piirtäminen onnistuu käsityönä, mutta kuvion muuntelu helpottuu ohjelmoimalla. Oivallinen työväline spirolateraalien tuottamiseen on kilpikonnagrafiikka. Jo pienelläkin ohjelmalla saadaan aikaan monenmoista. Esimerkiksi seuraavassa Logo-kielen syntaksilla kirjoitetussa rekursiivisessa ohjelmassa [6] on kolme parametria: koon määräävä SIVU, muodon määräävä KULMA sekä janojen pituuden ja lukumäärän määräävä LISTA.

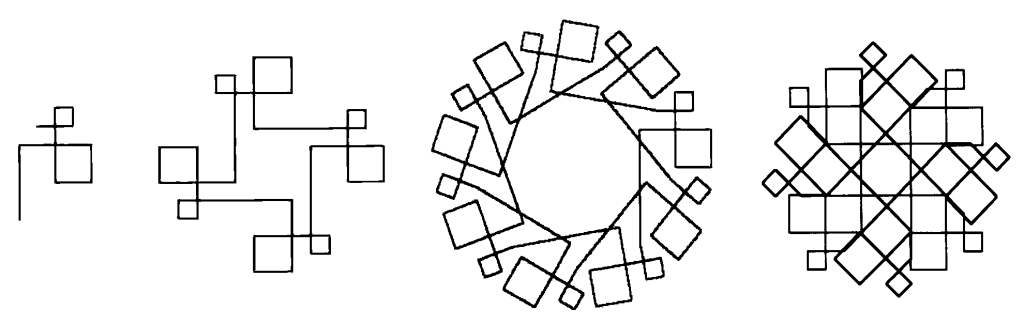
         TO SPI :SIVU :KULMA :LISTA

                   IF EMPTYP :LISTA [STOP]

                   FORWARD :SIVU * FIRST :LISTA

                   RIGHT :KULMA

                   SPI :SIVU :KULMA BUTFIRST :LISTA

         END

Kun lista on [1 2 3 4 5] ja kääntymiskulma 90° saadaan spiraali (kuva 4, vasen). Jos listaa jatketaan peräkkäisillä luonnollisilla luvuilla, niin spiraali kasvaa vastaavasti. Jos tämä ohjelma toteutetaankin samaa listaa käyttäen useamman kerran peräkkäin, saadaan monimutkaisempia kierrekuvioita (kuva 4, osakuvat 2–4 vasemmalta lukien). Mielenkiintoista on pohtia, milloin tuloksena on suljettu murtoviiva. Toisessa osakuvassa oikealta listana on [1 8 2 7 5], mikä on aika helppoa todeta kuvasta. Ohjelmakutsu on sama

         SPI 20 90 :LISTA

kuin edellä. On ehkä helppoa huomata, kuinka monta kertaa tämä on toteutettu peräkkäin oikeanpuoleista osakuvaa varten. Millaiset kuviot mahdettaisiin saada, jos ohjelma toteutettaisiin neljä kertaa peräkkäin samoilla listoilla, mutta kääntymiskulma olisikin 120°? Tai 160°? Kuinka monta kertaa ohjelma pitäisi toteuttaa peräkkäin, jotta saataisiin suljettu murtoviiva, kun kääntymiskulma on 160°? Onko tämä lukumäärä sama kummallekin listalle?

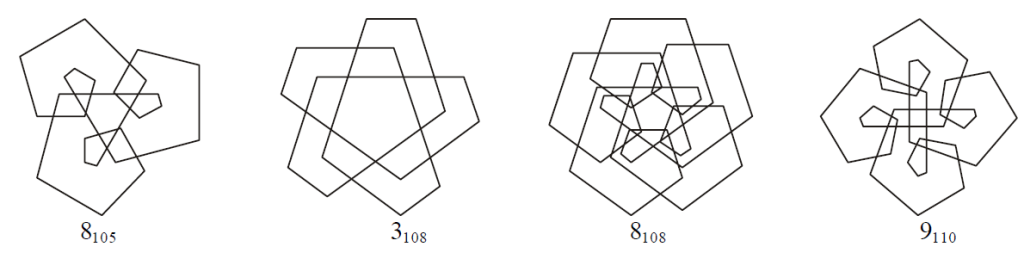
Kierrekuvioista (spirolateraaleista) on kirjoitettu paljon vielä myöhemminkin. Esimerkiksi Krawczyk [7] on tutkinut sellaisia, joissa kääntymiskulma on jotain muuta kuin 90° (kuva 5). Joitakin dynaamisia spirolateraaleja on myös GeoGebra-materiaaleissa [8].

Lähteitä ja lisää luettavaa

[1] Wikipedia-artikkeli Spirolateral osoitteessa https://en.wikipedia.org/wiki/Spirolateral.

[2] Odds, Frank C. (1973): Spirolaterals. The Mathematics Teacher, Vol. 66, No. 2, p. 121–124. https://www.jstor.org/stable/0e51f14d-47c2-3be9-9ce6-91be7d1b26fb?read-now=1&seq=4

[3] Gardner, Martin (1973)): Mathematical Games — Patterson’s Worms article. Scientific American, Vol. 229, No. 5 , s. 116–123. Saatavissa myös verkosta osoitteesta [4] Esimerkiksi Abelson, Harold ja diSessa, Andrea (1986): Turtle Geometry, s. 3–54. MIT Press.

[5] Riekkinen, Tuomo (2023): Spirolateraalit – Matemaattista taidetta kilpikonnagrafiikalla. Dimensio 22.8.2023. Osoitteessa https://dimensiolehti.fi/spirolateraalit-matemaattista-taidetta-kilpikonnagrafiikalla/

[6] Fisher, William ja Campbell, Richard (1991): Investigating Spirolaterals through LOGO. The College Mathematics Journal, Vol. 22, No. 2, s. 148-159 [7] Krawczyk, Robert J. (2000) The Art Of Spirolaterals. Illinois Institute of Technology. Osoitteessa https://www.researchgate.net/publication/2808257_The_Art_Of_Spirolaterals

[8] Joitakin spirolateraalitöitä löydät haulla https://www.geogebra.org/search/spirolateral