Matemaattisia taikoja ja variaatioita muistilehtiöstäni, osa 3: Suklaakarkkeja sammosta
Suklaakarkkeja sammosta – Lisää matemaattisia taikatemppuja ja työkaluja hauskempaan opetukseen ilmestyi vuonna 2019, vuosi ensimmäisen kirjan ilmestymisestä. Tällä kertaa kansien väliin tuli 206 sivua ja yli 70 matemaattista taikatemppua. Mukana on oma kappale seinäkalentereilla tehtäville taikatempuille, täynnä erittäin hyvää päässälaskuharjoittelua ja oman kappale pinta-aloista ja niihin liittyvistä paradokseista. Korttitempuissa on mukana temppu, jota pidän edelleen yhtenä parhaimmista niin kutsutuista itsestään toimivista korttitempuista (Pakka vie perille, sivut 147–150.). Esitän tuota edelleen niillä keikoilla, joissa on mahdollisuus tehdä katsojille korttitemppuja.

Tällä kertaa katsomme jotain sellaista, joka poikkea täysin kirjan muusta sisällöstä. Minua on aina kiehtonut ideat, joissa todellisuutta muokataan katsojan valinnan mukaan. Tämän tyyppinen temppu sopisi erittäin hyvin tiedekerhoon mutta myös oppitunnille, jossa opetetaan ohjelmointeja. Ohjelmoinnillakin on tarkoitus päätyä haluttuun lopputulokseen valitsemalla oikeanlaiset komennot. Esimerkki todellisuutta muokkaavasta tempusta on Suklaakarkkeja Sammosta kirjan suvulla 22–24 ja se on nimeltään: Milloin jokin on kolme? Otsikon alla on itseasiassa kaksi temppua, joissa idea on sama: katsoja tekee valinnan, ja taikuri kertoo ja todistaa, että valinta oli juuri se, mihin taikuri halusi hänen päätyvän. Taikurin selitykset muuttuvat katsojan valinnan mukaan. Katsojalle kerrotaan vain yksi selitys, joten hän ei tiedä, että olisi saanut toisen selityksen tekemällä toisenlaisen valinnan.
Ennustus määritellään oikeaksi vasta kun katsoja tehnyt valintansa. Ensimmäisessä tempussa katsojan kykyä osua oikeaan testataan kahdella pöydälle jaetulla pienellä korttipinolla. Katsoja päätyy aina seiskapakkaan. Toinen temppu liittyy tempun otsikkoon, Milloin jokin on kolme? Katsoja valitsee neljästä vaihtoehdosta aina kolmospinon.
Halusin tehdä tuosta versiossa vieläkin laajemman, viiden pinon ennustuksen. Törmäsin metodin rakenteelliseen ongelmaan (siitä myöhemmin), enkä keksinyt oikea ratkaisua vasta kuin kirjan julkaiseminen jälkeen. En ole julkaissut tätä versiota aiemmin missään, joten se sopii oikein hyvin tänne Dimensioon.
Milloin neljä on neljä?
Taikuri jakaa pöydälle viisi pientä korttipinoa. Taikuri pyytää katsojaa valitsemaan yhden pinoista.
Ennen kuin katsoja tekee valintansa, taikuri sanoo tietävänsä etukäteen, mikä tämä valinta on. Taikuri ilmoittaa, että katsoja tulee valitsemaan nelospinon. Katsoja tekee valintansa ja osoittaa yhtä pinoista, ja taikuri todistaa, että juuri se on nelospino.
Selityksiä
Kortit ovat pöydällä rivissä. Katsoja on toisella puolella pöytää. Taikurilla on mielessään jokaiselle pinolle oma selityksensä ja todistus, joka erottaa sen muista pinoista. Katsotaan kaikki mahdolliset tilanteet lävitse.
KATSOJA VALITSEE ENSIMMÄISEN PINON VASEMMALTA
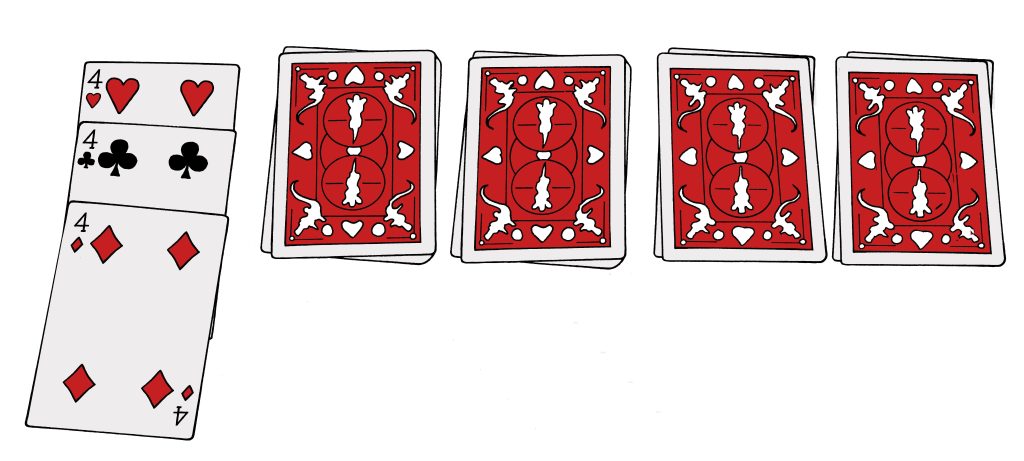
Taikuri kääntää ensimmäisen pinon kortit ympäri. Pinossa on vain nelosia, herttaneljä, ristineljä ja pataneljä, joten katsoja valitsi selvästi nelospinon. Taikuri kääntelee muut pinot ympäri osoittaen, että muualla ei ole lainkaan nelosia.
KATSOJA VALITSEE TOISEN PINON VASEMMALTA
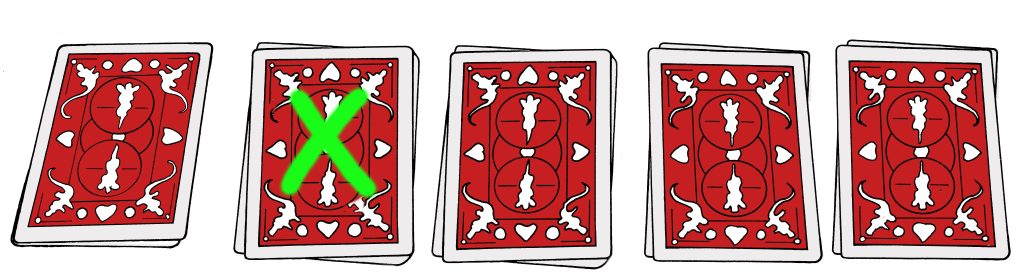
Katsoja osoittaa taikurin suunnalta katsottuna kakkospinoa. Kuvassa tämä on merkattu vihreällä ruksilla. Taikuri laskee pinoja oikealta vasemmalle ja päätyy neljäntenä katsojan osoittamaan pinoon. Näin tulee pinoja laskemalla todistettua, että katsojan valinta oli nelospino. Katsoja on pöydän toisella puolella, joten laskutapa on hänelle sieltä suunnalta looginen, vasemmalta oikealle. Tilanne ei vaadi muita todisteluita, eikä korttien tarkastelua. Pinossa voi olla mikä tahansa määrä kortteja, kunhan siinä ei ole neljää pelikorttia.
KATSOJA VALITSEE KESKIMMÄISEN PINON
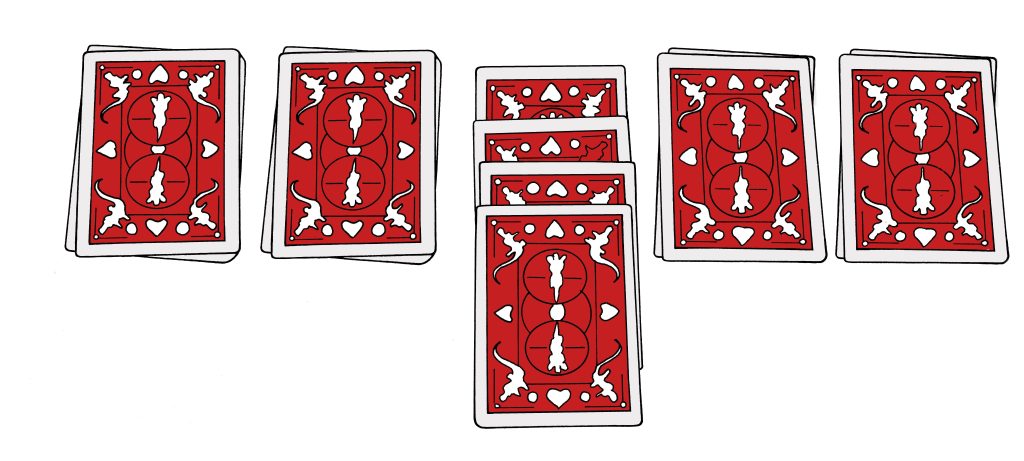
Taikuri levittää katsojan osoittamaa keskimmäistä pinoa. Huomataan, että siinä pinossa on neljä korttia. Kun muita pinoja levitetään, huomataan että niissä on joko enemmän tai vähemmän kuin neljä pelikorttia. Vain keskimmäisessä pinossa on neljä korttia. Tämä on siis selkeästi nelospino.
KATSOJA VALITSEE NELJÄNNEN PINON VASEMMALTA LASKIEN
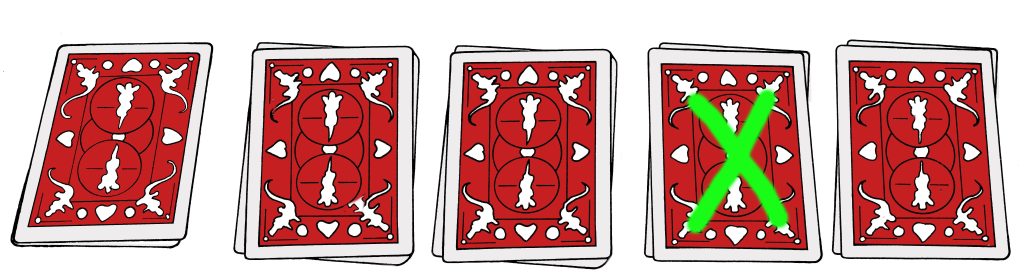
Otsikossa piilee vastaus. Kun pinoja lasketaan taikurin suunnalta vasemmalta oikealle, katsojan valinta on neljäs pino. Jos katsoja ihmettelee laskemissuuntaa toteamalla, että hän laskisi pinot toiselta suunnalta, niin taikuri toteaa, että nämä ovat hänen korttinsa ja pinot, joten noudatetaan hänen laskutapaansa. Katsojan valinta on merkitty kuvaan vihreällä ruksilla. Pinossa voi olla mikä tahansa määrä kortteja, kunhan siinä ei ole neljää pelikorttia.
KATSOJA VALITSEE VIIMEISEN PINON
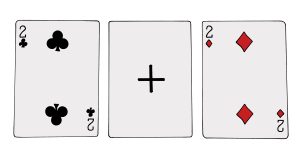
Katsoja osoittaa valinnakseen hänen suunnaltaan rivin ensimmäisen pinon ja katsojan suunnalta tarkasteltuna rivin oikeanpuoleisimman pinon. kuvassa tämä kolmen kortin pino on jo käännetty kuvapuoli ylöspäin. Pinossa on kolme korttia, kaksi kakkosta ja erikoiskortti, joka on taustaltaan tavallinen pelikortti mutta kuvapuoleltaan tyhjä. Kortin keskelle on piirretty + merkki laskutoimitukseksi.
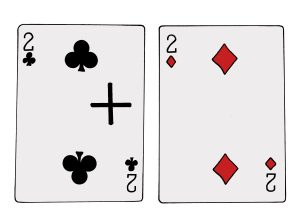
Korteista syntyy laskutoimitus 2 + 2 = 4 joten tämä on selvästi nelospino. Viereisten pinojen tarkastelu osoittaa, että muualla ei ole laskutehtäviä tarjolla. Jos et halua lähteä hankkimaan pelkästään tätä temppua vasten pelikortteja, joissa ei ole kuvapuolta lainkaan (niitäkin on myynnissä!), voit kirjoittaa plus -merkin toisen kakkosen vasempaan laitaan, kuten viereisessä kuvassa on tehty. Tällöin viimeisessä pinossa on vain kaksi korttia.
KORTTIEN NÄYTTÄMISESTÄ
Jos katsoja valitsee pinon, jossa on kolme nelosta, käännät nämä kuvapuoli ylöspäin. Voit vapaasti esitellä muidenkin korttien kuvapuolia, mutta pino, jossa on kakkoset ja plussamerkki, kannattaa kääntää yhtä aikaa nippuna ja levittää vain hiukan, jottei plussamerkki ja muutoin täysin valkoinen kortti ponnahda näkyviin. Katsojat kiinnittävät ensiksi käännettyihin tarkempaa huomiota, joten kun viimeisenä näytetään huolimattoman oloisesti tämä kakkosia sisältävä pino, keskimmäiseen korttiin ei kukaan kiinnitä huomiota, eikä siihen, että kortti näytetään vain osittain. Jos nyt yleensä mitään etsii, niin katsoja etsii tässä vaiheessa nipullista muita nelosia, eikä kiinnitä mihinkään muuhun huomiota. Jos olet laittanut plusmerkin kakkosen laitaan, on tämän merkin piilottaminen toisella kakkosella helpompaa.
Jos katsoja valitsee keskimmäisen pakan, on todella helppo näyttää, että muissa pinoissa on joko enemmän tai vähemmän kuin neljä korttia. Yhdenkään pinon kuvapuolia ei tarvitse esitellä.
Jos katsoja valitsee pinon, joka lasketaan neljänneksi pinoksi (jommaltakummalta suunnalta), muiden pinon kortteja ei tarvitse esitellä.
Jos katsoja valitsee pinon, jossa on kakkoset ja plusmerkkikortti, kannattaa muut kortit kerätä pöydältä yhteen kansaan ja levittää huolimattomasti kaikki kortit yhtä aikaa näkyville. Tällöin katsojat näkevät, että muita laskumerkkikortteja ei ole. Samalla kolmen neloskortin nippu hukkuu muiden korttien sekaan, eikä herätä ihmetystä.
RAKENTEELLINEN ONGELMA
Milloin neljä on neljä? tempun suunnittelun jarruna oli pino, jossa on vain nelosia. Tuntui luonnolliselta, että siinä pinossa pitää olla kaikki neloset, neljä kappaletta. Pino oli tällöin yhtä suuri kuin se pino, jossa on neljä pelikorttia. Tässä versiossa ei voi olla kahta neljän kortin pinoa. Kesti yllättävän kauan keksiä, että neloskorttien pinossa voi aivan hyvin olla kolme nelosta. Mielessäni kävi idea tehdä tämä otsikolla: Milloin viisi on viisi. Tällöin pinoja olisi edelleen ollut viisi. Laitapinoihin mennään laskemalla ja keskellä yhdessä pinossa olisi kaikki neljä vitosta, yhdessä pinossa viisi korttia ja yhdessä tuollainen laskutoimitusjuttu. Itseäni kiehtoi parempana ajatus, että jos pinoja laskemalla päädytään katsojan valitsemaan pinoon, pino on rivin sisällä, ei päädyssä. Mutta jos sinua ei häiritse laskea koko riviä loppuun saakka päästäksesi katsojan valintaan, voit toki askarrella itsellesi: Milloin viisi on viisi tempun.
HISTORIAA
Temppu, jossa katsojan valinta muokkaa lopputulosta löytyy ainakin Geo DeLaWrecen ja James ”Kater” Thompsonin kirjasta Modern Card Effects (1920) nimellä The Seven Card Trick, sekä Walter B Gibsonin kirjasta Popular Card Tricks (1928) nimellä Heap of the Three. Myöhemmin Walter Gibson palaa saman idean pariin hiukan erilaisella versiolla kirjassaan Professional Magic for Amateurs (1948). Viimeksi mainitusta julkaisin oman versioni Viiriäisiä ja suklaakarkkeja nimisellä Facebook-sivustollani 7.4.2021. Sivusto on tarkoitettu kirjojeni lukijoille ja myös täällä Dimensiossa julkaisemieni juttujen lukijoille. Mukaan pääset, kun haet Facebookissa hakusanalla Viiriäisiä ja suklaakarkkeja ja sivustolla klikkaat pyyntöä päästä porukkaan mukaan.
Suklaakarkkeja Sammosta -kirjani lisäksi samaa todellisuutta muokkaavaa menetelmää käytetään uusimmassa kirjassani Pakottavia taulukoita ja paradoksipapereita sivulta 250 nimellä Pelikortteja ja tulitikkuja. Siinä tempussa on lopulta kaksitoista ratkaisua katsojan valintoihin. Temppu vaatinee taikurilta (oppilaalta) hereillä oloa ja nopeita päässälaskuja ja hyvää muistia. Tämänkertainen Milloin neljä on neljä? on sekoitukseni lainattuja ja itse keksimiäni ideoita klassikkotemppuun.
Martti Sirén on hämeenlinnalainen taikuri, tietokirjailija, työpajakouluttaja, taikuuden historian penkoja ja tarinoiden kertoja, myös todellisuutta muokkaavien tarinoiden kertoja.
Hän on kirjoittanut neljä kirjaa matemaattisista taikatempuista ja pitänyt matemaattisten taikatemppujen työpajoja opettajille yli viidentoista vuoden ajan.
Osa 1: Pakottavia taulukoita ja paradoksipapereita Dimensio-lehdessä 8.9.2022
Osa 2: Viisi viiriäistä ja kaksi kelmiä Dimensio-lehdessä 20.11.2022
Tilaa Dimension uutiskirje – saat sähköpostiisi aina kuunvaihteessa koosteen tuoreimmista artikkeleista







