Affiinikuvauksia Geogebralla

Affiinikuvaus kuvaa tason pistejoukon kääntäen, venyttäen, siirtäen joukon paikkaa tai skaalaten joukon kokoa. Sillä on kolme perusominaisuutta: se kuvaa suoran suoraksi ja yhdensuuntaiset suorat yhdensuuntaisiksi sekä säilyttää janojen osien suhteet. Sellainen affiinikuvaus, joka säilyttää origon paikan, on myös lineaarikuvaus. Esimerkki tällaisista kuvauksista on suorakulmaiseen koordinaatistoon piirretyn kuvan tai kuvaajan kuvaaminen vinokulmaiseen koordinaatistoon. Näitä tutkitaan tässä jutussa.

Bing-haku affiinikuvaus antaa alun toista tuhatta tulosta, vastaava englanninkielinen yli kaksi miljoonaa. Selitykset alkavat useimmiten yleisellä, muodollisella määritelmällä. Tässä jutussa käytän apuvälineenä Geogebraa, sillä se tarjoaa mahdollisuuden tutkia asiaa esimerkkien avulla sekä synteettisesti että analyyttisesti ilman, että on tarpeen lähteä muodollisesta määritelmästä. Yleisten käsitteiden nimiä ei siis käytetä, vaan piirrellään kuvia, toisin sanoen tutkitaan, minkälaisia suorakulmaiseen koordinaatistoon piirrettyjen objektien kuvat ovat vinokulmaisessa koordinatistossa. Tämä on ainoa uusi käsite, joka tarvitaan. Y-akselin kääntäminen vinoon on konkreettinen toimi, joka on koululaisenkin ymmärrettävissä helposti suorakulmaisen koordinaatiston idean perusteella.

Tätä oppimisen alkuvaihetta nimitetään joskus tutustumiseksi tai perushahmotukseksi. Se antaa niitä konkreettisia mielikuvia, jotka luovat merkityksiä muodollisten määritelmien ymmärtämisen pohjaksi.  Tällainen työskentely kehittää matemaattista ajattelua ja lujittaa oppijan matematiikkakuvaa, vaikka nämä asiat eivät sisällykään koulukursseihin teorialtaan eivätkä määriteltäviltä käsitteiltään edes lukiossa.

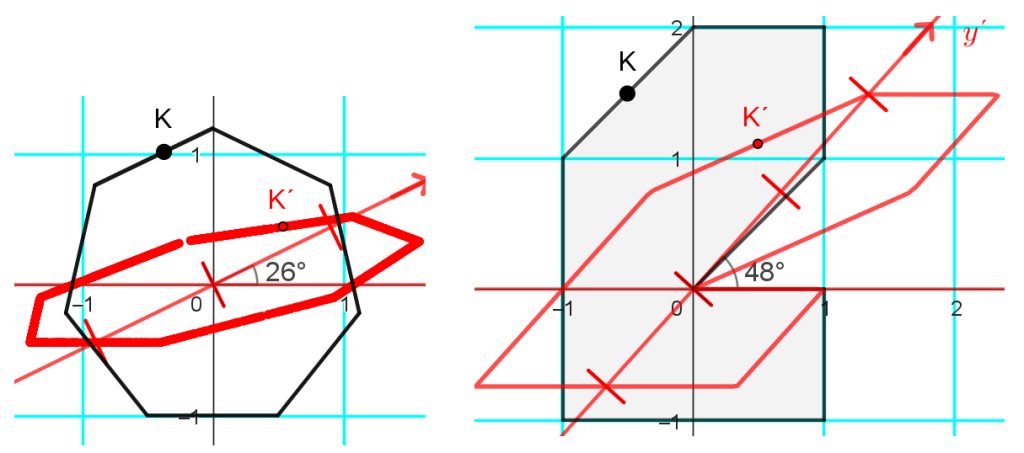
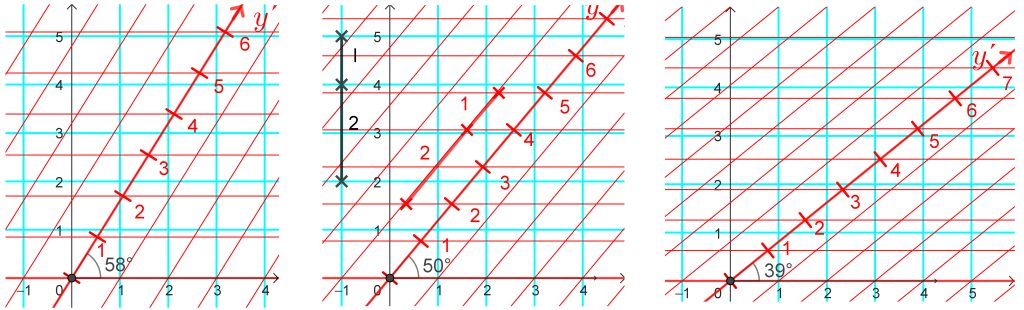
Katsotaanpa ensin vaikka koordinaattiakseleita ja -ruudustoja. Kuvissa on päällekkäin suorakulmainen koordinaatisto (neliöruudusto turkoosilla) ja vinokulmainen koordinaatisto (neljäkäsruudusto punaisella, kolme eri kallistuskulmaa) x-akseli yhteisenä. Vinokulmaisen koordinaatiston ruudustoviivat voidaan ajatella suorakulmaisen koordinaatiston ruudustoviivojen kuviksi kuvauksessa, joka kääntää y-akselin vinoon. Keskimmäisessä kuvassa on ruuduston lisäksi suorakulmaisen koordinaatiston jana (musta pystyjana) jaettuna suhteessa 1 : 2 ja sen kuva vinokulmaisessa koordinaatistossa (punainen vino jana; jakosuhde säilyy, vain janan suunta muuttuu).

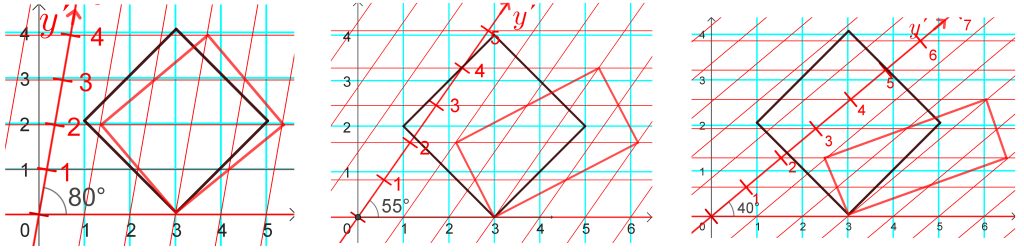
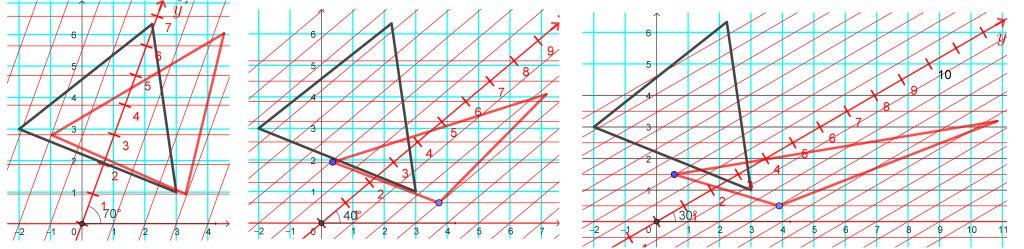
Koska suorat kuvautuvat affiinimuunnoksessa suoriksi, niin janat kuvautuvat janoiksi ja monikulmiot monikulmioiksi. Seuraavissa kahdessa kuvassa on monikulmioita (mustat) sekä niiden kuvia (punaiset) erisuuruisilla kallistuksilla. Neliön kuvista nähdään, että vastakkaisten sivujen yhdensuuntaisuus säilyy. Kolmion kuvat voidaan piirtää kuvaamalla vain kärkipisteet ja yhdistämällä ne sivujanoilla, koska affiinikuvaus kuvaa suoran suoraksi.

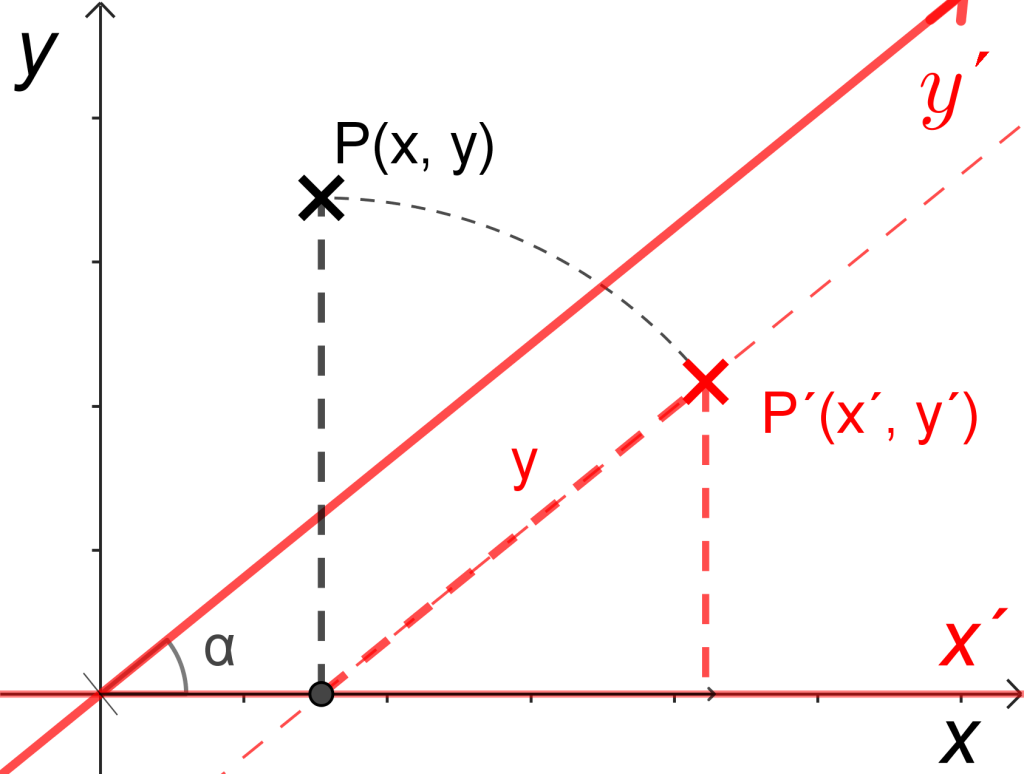
Tähän asti kuvaukset on voitu tehdä piirtämällä synteettisen geometrian tapaan ilman mitään laskuja. Käyräviivaisten kuvioiden ja funktioiden kuvaajien piirtämiseen tarvitaan sen sijaan vahvempia analyyttisen geometrian menetelmiä. Suorakulmaisessa koordinaatistossa olevan pisteen P(x, y) kuvan P´(x´, y´) koodinaatit saadaan lausekkeista

x´ = x + y cos(α)
y´ = y sin(α)

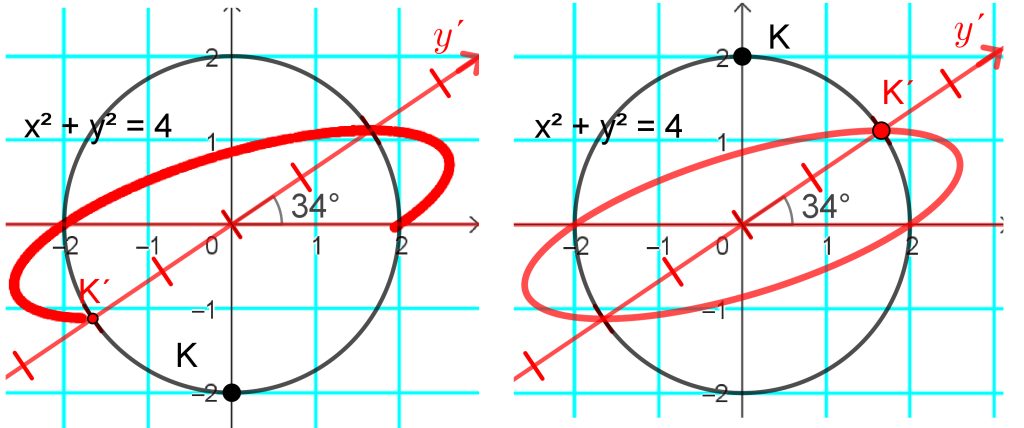
Suorakulmaisessa koordinaatistossa olevan käyräviivaisen kuvion kuvan piirtämiseen on kaksi mahdollisuutta. Merkitään kuviolle piste K ja luodaan edellä olevien koordinaattien avulla sen kuva K´. Ensimmäisessä tavassa valitaan pisteen K´ tilaksi Näytä jälki. Kun nyt pistettä K siirretään pitkin kuviota, niin K´ piirtää sen kuvan. Seuraavassa kuvassa (vasemmanpuoleinen) on tulos, kun pistettä K on siirretty ympyrää pitkin x-akselilta kolme neljäsosakierrosta vastapäivään. Toinen ja nopeampi tapa on se, että piirretään pisteen K´ ura pisteen K suhteen (oikeanpuoleinen osakuva). Tähän jälkimmäiseen ei tarvita muuta kuin objektin  Ura valitseminen (neljäs toimintovalikko vasemmalta). Tätä tapaa olen käyttänyt seuraavissa funktioiden kuvaajien kuvissa.

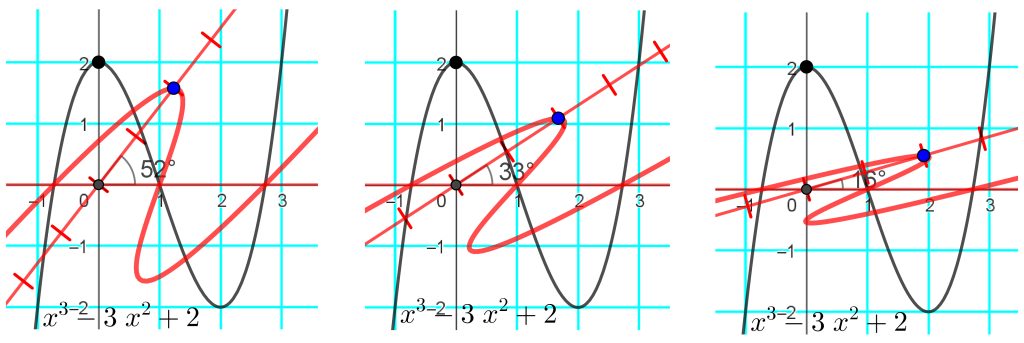
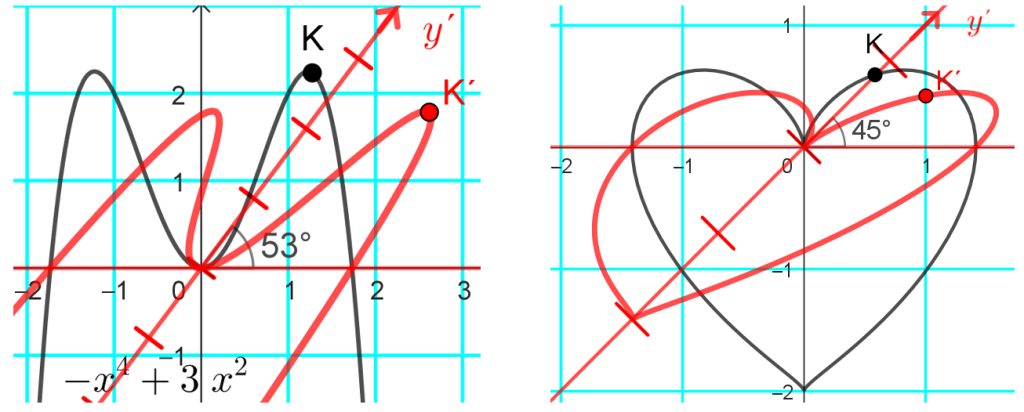
Kun tähän asti on päästy, niin jatko on helppoa. Ei tarvitse piirtää seuraavia kuvia alusta lähtien, vaan riittää että määrittelee alkuperäisen objektin uudestaan objektin ominaisuuksissa. Myös parametrimuotoinen määrittely kelpaa. Oikeanpuoleinen sydänkäyrä on

$ \left(\sqrt{2}\sin^3\left(t\right){,}-\cos^3\left(t\right)-\cos^2\left(t\right)+2\cos\left(t\right)\right). $

Eikä kuvattavaksi kuvioksi sovi pelkästään käyrä tai funktion kuvaaja, vaan sama uraperiaate toimii myös geometrisille kuvioille. Silloin riittää, että kirjoittaa vain kuvion nimen kuvattavan kuvion määrittelyikkunaan. Ura toimii silloinkin!